Constructing the climatology consists of several steps which are briefly outlined here. First, the climatology time frame, spatial and temporal resolution, and observation types are selected. The automated quality control procedure is applied to the original temperature and salinity profiles, which are subsequently interpolated on a predefined set of depth levels. The interpolated profiles are then averaged in 1∕4^∘ bins on a monthly basis, with the binned data providing the input for the spatial optimal interpolation. Highly smooth gridded fields of water density, temperature, and salinity obtained by distance weighted averaging are generated and used as the first guess fields required by the objective mapping method. At each grid point, the covariance matrices for optimal parameter estimation take account of both the distance between the data points and the difference in the bottom depth, so that along isobath observations become greater weights than across isobath observations. It is assumed that the fields to be analyzed and the noise in the data are uncorrelated. Two versions of the climatology are subsequently constructed in two steps: (1) the isobaric climatology with the optimal interpolation (mapping) performed on depth levels and (2) the isopycnal climatology where mapping is carried out on local density surfaces. The new climatology is compared with the last version of the NOAA WOA13 atlas, which has the same temporal and spatial resolution and also includes Argo profiles. Finally, the new climatology is used as a reference for the calculation of the ocean heat content anomaly time series. It should be noted that even with the Argo data included, the 0.25^∘ resolution should be considered as a nominal resolution for the greater part of the world ocean. Nevertheless, the increased resolution permits a better description of the ocean, both in the regions of complicated topography like the Indonesian seas and in the data abundant areas (Boyer et al., 2005).

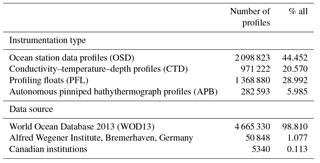
The WOD13 database (Boyer et al., 2013) (including the January 2017 update) served as the main data source for the WAGHC climatology. The profiles of the four instrumentation types were used: ocean station data (OSD), conductivity–temperature–depth (CTD), Argo profiling floats (PFL), and the autonomous pinniped bathythermograph data (APB). The latter were only used in the Southern Hemisphere where data coverage is generally poorer compared to the Northern Hemisphere. All four data types normally report both temperature and salinity. As both of these parameters are required for the spatial interpolation on isopycnal surfaces, the expendable (XBT) and mechanical (MBT) bathythermograph data were not used. We then added 50 848 profiles obtained from the Alfred Wegener Institute, Bremerhaven, and 5340 profiles received from different institutions in Canada to the existing 4 665 330 temperature/salinity profiles from the WOD13. These two additional datasets helped to significantly improve the data basis for northern polar regions. Table 1 gives details regarding the data types and data sources that contributed to the WAGHC. The dismissal of some instrumentation types along with the stringent quality control criteria explain why the total number of retained profiles is less than the approximate 5.4 million salinity profiles available in the WOD13 archive.

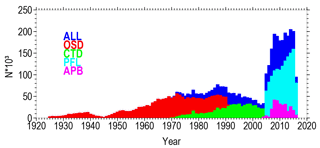
Figure 1 shows the yearly number of profiles of each data type retained after quality control. Before 1990 OSD profiles prevail, whilst CTDs are the main data type between 1990 and 2003. In later years, observations were mostly delivered by Argo floats, with the implementation of Argo floats being marked by a step-like increase in the number of available data.

Table 1Instrumentation types and data sources that contributed to the WAGHC climatology.

Download Print Version | Download XLSX

Figure 1Yearly number of profiles for each data type.

Download

In general, for most of the global ocean, we used data from 1985 (the beginning of the pre-WOCE hydrographic programme) to the present; thus, we have incorporated data from the last 32 years, which is close to the 30-year period for calculating climate norms that is recommended by the World Meteorological Organization. In some regions (mostly at high latitudes and in several marginal seas) there are still no or insufficient data, meaning that older data (since 1925) were utilized. However, the time frame for the data selection was narrower, especially within the upper 2 km Argo float depth range.

Quality control is important for the construction of the climatology. Due to the large volume of data, an automated quality control (AQC) procedure was developed. It consists of a suite of the following quality checks:

1. crude parameter range check,

2. spike check,

3. constant value check,

4. multiple extrema check,

5. vertical gradient range check,

6. local climatological range check,

7. sample depth vs. local digital bathymetry check,

8. percentage of rejected (flagged) observed levels.

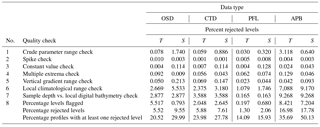
Before quality control, the observed depth levels were checked and reordered in increasing order if necessary. For the purpose of the initial tuning of the AQC procedure and for the final assessment of data quality, a diagnostic tool was developed which provides the statistics of rejected (flagged) data vs. time, observation depth, and bottom depth. The AQC procedure is applied to original profile data separately for temperature and salinity. Table 2 contains statistics of the data rejection rates. According to the statistics, Argo float data are characterized by the lowest rejection rate, followed by CTD, OSD, and APB data. The application of the local climatological range check and the sample level depth vs. local bathymetry quality checks results in the largest percentages of outliers.

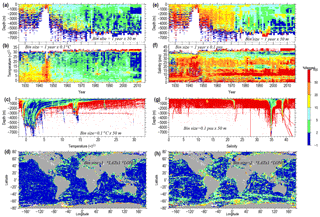
The overall performance of the AQC procedure is illustrated by two-dimensional histograms (Fig. 2). For both temperature and salinity, the time–depth histograms indicate a decrease of data rejection rates with time. The highest rejection rate is observed around the Second World War and may be attributed to the conditions being generally unfavorable for conducting high quality observations. A significant improvement in the quality of temperature and especially salinity observations took place due to the introduction of CTDs and electronic salinometers at the beginning of 1970s; the next data quality improvement was due to the introduction of profiling floats in the mid-2000s. The AQC procedure identified 3.745 % and 5.255 % of observed levels for temperature and salinity, respectively, as outliers, whereas for 14.201 % and 18.167 % of temperature and salinity profiles, respectively, at least one observed level outlier was identified. Further details regarding the quality control procedure are given in the Appendix. The implementation of manual quality control was restricted to several areas in the Arctic Ocean that had very poor data coverage.

Table 2Data rejection rate for the automated quality control procedure.

Download Print Version | Download XLSX

Figure 2Temperature (a–d) and salinity (e–h) data rejection rates (all instrument types).

Download

The quality-controlled observed temperature and salinity profiles were finally interpolated on 65 unevenly spaced “standard” levels between the surface and 6750 m. The depth interval between the levels increased linearly with depth, so that a better vertical resolution was achieved in the upper layers, where higher vertical property gradients typically occur. Only levels with both temperature and salinity that passed all quality checks were retained for vertical interpolation using the weighted-parabola method by Reiniger and Ross (1968). The interpolation was not performed where the spacing between two levels exceeded the depth-dependent threshold value h: h=20 m within the upper 50m layer, $h=\mathrm{20}+\mathrm{0.24}\cdot z$ between 50 and 2000 m (z is the mean distance between the two levels in meters), and h=500 m for z>2000 m. The limitation on the spacing between the observed levels is necessary to minimize the creation of artificial water masses due to the interpolation procedure.

After the mid-2000s, the majority of the temperature/salinity profiles come from Argo floats (Fig. 1). Since the floats only measure within the upper 2000 m layer, a step-like decrease in the data coverage occurs around the 2000 m level, which would create a strong bias towards the observations above 2000 m when spatial interpolation is performed on isopycnal surfaces. To avoid this artifact, the profile extension method was developed. The method is based on the observational fact that the local temperature and salinity values are fairly constant below the main thermocline. First, in the vicinity of each profile potentially suitable for extrapolation, up to 10 deep CTD and OSD profiles are selected and the average deep profile is calculated using distance weighted mean values at each standard level (the influence radius for the deep profile selection does not exceed 333 km). For the last observed level Z_m (the merging depth) of the profiles subject to extrapolation the temperature and salinity offsets (DT_o and DS_o) relative to the mean profile are calculated. If the parameter offset for the merging depth does not exceed a predefined threshold value (0.05 ^∘C for temperature and 0.01 for salinity), and if Z_m>1898 m (the deepest WAGHC standard depth level within the Argo depth range), the profile is considered to be suitable for extrapolation. The average profile is then modified as follows: at each depth level Z>Z_m the offset value DP = DP${}_{\mathrm{o}}[\mathrm{1}-(Z-Z_m)/(Z_{\max }-Z_{\mathrm{m}})$] is subtracted from the average parameter value (temperature or salinity). The modified mean profile is used to extrapolate the original profile below the level Z_m.

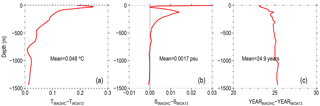
Figure 3 illustrates the extrapolation procedure for three arbitrarily selected full-depth CTD profiles. In order to estimate the average extrapolation error, we selected 52 672 full-depth CTD and OSD profiles deeper than 2200 m obtained after 1984 and interpolated on standard levels. The extrapolation procedure was then applied to all of these profiles truncated at levels equal to or deeper than 1898 m. The respective mean absolute difference between the extrapolated and the original full-depth profile decrease with depth and are in the range between 0.03 ^∘C at 3000 m and 0.002 ^∘C at 6000 m for temperature and between 0.003 psu and 0.001 psu for salinity (Fig. 4).

Finally, the extrapolation procedure was applied to 720 839 quality controlled OSD, CTD, and PFL profiles that were obtained after 1984 and had their last level at or deeper then 1898 m. For most of the ocean area, the percentage of extrapolated levels exceeds 20 % from the total number of levels, with Argo extrapolated profiles comprising the largest group. The spatial distribution of full-depth and extrapolated profiles is shown in Fig. 5 along with the percentage of the interpolated levels and extrapolated profile frequency distributions vs. the number of extrapolated levels and the year of observation.

The significantly increased data basis since the introduction of the Argo floats permits a better temporal and spatial resolution compared to the earlier WOCE Global Hydrographic Climatology (WGHC) (Gouretski and Koltermann, 2004). For each standard depth surface, the quality controlled vertically interpolated/extrapolated data were gridded by bin-averaging the data separately for each calender month in each 1∕4^∘ grid cell. The binning procedure serves two purposes. Firstly, the binning reduces the overall number of observations and, secondly, it reduces noise in the data. The thinning of the input profiles permits the application of the classical optimal interpolation method without the use of a fast multiscale optimal interpolation algorithm proposed by Menemelis et al. (1997).

With the aim of producing a climatology for the most data abundant recent years, the data selection for each spatial bin was performed iteratively, with the data being selected first for the time period from 1985 to 2016; thus, the WOCE hydrographic survey was embedded in the analysis. If no data were available for a particular grid node, the time period was extended to 1957–2016. For a small fraction of the grid nodes, all data since 1925 were used to produce the bin-averaged values. The percentage of spatial monthly bins populated with two or more observations decreased from 30 % in the upper several hundred meters to about 20 % at levels deeper than 2000 m.

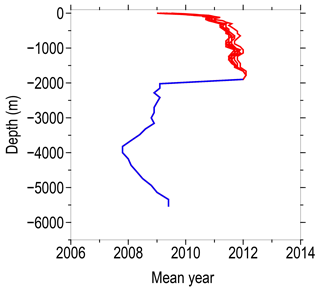
The mean climatological year changes with depth, in the range from 2007 to 2011. For the upper 2 km layer where the Argo float data prevail, the climatological year is within the 3-year range between 2009 and 2011 (Fig. 6). Below the Argo depth range, the mean year is within the range from 2007 to 2009. Differences between the mean climatological year for different calendar months do not exceed 1 year. It is important to mention that the WOA13 climatology is created by averaging six decadal climatologies between 1955 and 2012, with 1984 being the median year. This method prevents biases toward more recent and data abundant years. The difference between the median years of both climatologies does contribute to the temperature and salinity differences of the two gridded products and is discussed later in the text.

Figure 3Example of the profile extrapolation procedure for three arbitrarily selected CTD temperature (a) and salinity (b) profiles.

Download

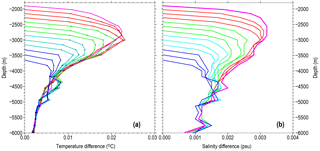
Figure 4Mean absolute difference between the observed and extrapolated profiles for temperature (a) and salinity (b) at different merging depths. The intersection of each difference profile with the y axis corresponds to the respective merging depth.

Download

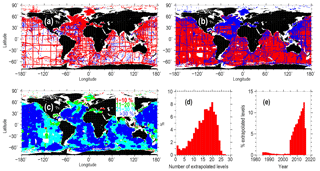
Figure 5(a) Positions of full-depth profiles used for the extrapolation procedure (blue – before 1985, red – after 1984); (b) positions of extrapolated profiles (red – Argo profiles, blue – non-Argo profiles); (c) percentage of extrapolated levels; (d) extrapolated profile frequency distribution vs. the number of extrapolated levels; and (e) extrapolated profile frequency distribution vs. the year of observation.

Download

The contemporary database does not provide enough data to obtain bin-averaged values for each 1∕4^∘ monthly bin, meaning that an interpolation procedure to fill gaps is needed. The bin-averaged temperature and salinity profiles serve as inputs for the spatial optimal interpolation method, which is used here in the form suggested by Gandin (1963). For the optimal interpolation on isobaric surfaces, the normalized spatial covariance C_xyh of temperature and salinity was represented through the negative squared exponential:

where r_x and r_y are zonal and meridional distances between the two points, L_x and L_y are the zonal and meridional decorrelation scales, h is the depth difference between the two points, and H is the decorrelation depth scale. Outside of the ±20^∘ zonal belt around the Equator, L_x=L_y whereas, within this belt, L_x increases linearly from L_y at 20^∘ N and 20^oS to 4 L_y at the Equator, in order to account for the zonal elongation of correlation scale within the equatorial belt. The introduction of the (h∕H)² term in Eq. (1) represents the added distance penalty for crossing isobaths. The value of H was set to 2 km. Based on the evaluation of the test calculations the signal-to-noise variance ratio was chosen to be 0.5 as a trade-off between the smoothness and desirable feature resolution.

For the optimal interpolation on isopycnal surfaces the normalized spatial covariance C_xyz was also represented through the negative squared exponential:

where ℜ is the depth difference between the vertical positions of the same isopycnal surface, and Z=250 m is the decorrelation depth scale. The introduction of this term is aimed at reducing the depth bias that appears near the boundaries of the domain, where observations are biased to one side (above or below) of the analyzed grid level. The objective analysis is performed on deviations between the observations and first guess values. To provide the distance-weighted means for the first guess temperature, salinity, and density fields, Eq. (1) was used with L_x and L_y set to 555 km.

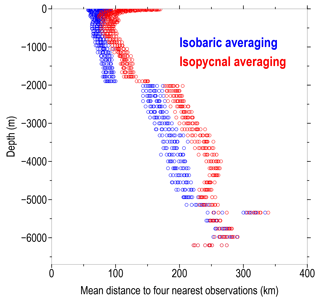
The spatial covariances of the analyzed temperature and salinity fields should be derived from available observations. However, the correlation length scale must at least be larger than the data spacing (Nuss and Tutley, 1994; Sokolov and Rintoul, 1999). We use the mean average distance to the four nearest bin-averaged neighbor profiles as the measure of data sparseness (Fig. 7). The distance between the observation points increases with depth from about 70–100 km within the upper 2000 m to about 200–300 km in the lower layer. These mean values were used as a guide for the choice of the decorrelation length scale for the optimum interpolation. After some experimenting, we decided on a decorrelation scale value of 333 km, which was used at all levels for the current version of the climatology (the decorrelation scale is the distance at which the autocorrelation function decreases to 1∕e times the value of the zero lag). As noted by Sokolov and Rintoul (1999), the optimal interpolation produces a spatial average of the analyzed parameters, acting as a low-pass filter.

During the first step, the isobaric climatology is constructed with the binned data being spatially interpolated at preselected standard levels for each calendar month. We do not perform spatial interpolation for temperature and salinity separately. Instead, to avoid the undesirable effect of artificial water mass production, we first perform spatial interpolation of sea water density. Subsequently the optimal estimate of temperature on isobaric surfaces is obtained. The interpolation of salinity is not performed: the salinity is inferred from the isobarically interpolated density and temperature values. We note, that the approach described above differs from the method used for the construction of earlier versions of the World Ocean Atlas (Levitus et al., 1994, 1998), where isobaric interpolation (averaging) was performed separately for temperature and salinity. The calculated density profiles are checked for hydrostatic stability and the stabilization is performed if necessary by introducing small adjustments to temperature and salinity.

Figure 6Area-mean climatological year vs. depth. Monthly values above 1900 m are shown in red.

Download

Figure 7The mean average distance to the four nearest bin-averaged profiles vs. depth.

Download

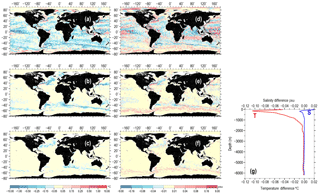
Figure 8Temperature (a–c) and salinity (d–f) differences between the isopycnally averaged and isobarically averaged WAGHC climatologies for selected depth levels in January: 150 m (a, d), 518 m (b, e), 1050 m (c, f); and area-averaged differences vs. depth (g).

Download

At each grid location, the stabilized isobarically averaged density profile defines the set of local density surfaces on which the interpolation of temperature is subsequently performed. As in the isobaric case, the salinity is inferred from density and temperature values.

The advantage of the isobaric method is that it can be applied in exactly the same way throughout the water column. However, the averaging (smoothing) of data along levels of constant depth does not correspond to the process of the water mass mixing in the real ocean which takes place along isopycnal, or more correctly along the neutral density surfaces. In contrast, the isopycnal averaging does not produce artificial water masses; however, in the regions where isopycnals outcrop at the surface or bottom, the isopycnally averaged parameters are biased toward the ocean interior (Schmidtko et al., 2013).

Differences between parameter distributions on selected levels between the isopycnally and isobarically averaged WAGHC climatologies are shown in Fig. 8a–e. As expected the largest differences occur in regions of strong spatial temperature and salinity gradients, like the Gulf Stream, the Kuroshio, Antarctic Circumpolar Current, and the equatorial and tropical Pacific Ocean. In such regions the absolute difference in temperature and salinity can exceed 1 ^∘C and 0.2 psu, respectively. The differences diminish with increasing depth. Thus, at the level of 1050 m, only the North Atlantic and the belt of the Antarctic Circumpolar Current show systematic differences exceeding 0.05 ^∘C and 0.01 psu for temperature and salinity, respectively. Integrated over the whole ocean area (Fig. 8g), the climatological isobaric temperature values are higher than the isopycnally averaged values. The same is true for the salinity except for the upper 100 m layer. Below 2000 m, typical absolute differences between the isobarically and isopycnally averaged temperature and salinity values remain below 0.25 ^∘C and 0.005 psu, respectively.

Figure 9Temperature (a–c) and salinity (d–f) isopycnal WAGHC climatology minus WOA13 climatology differences for selected depth levels in January: 150 m (a, d), 518 m (b, e), and 1050 m (c, f).

Download

We compared the WAGHC monthly temperature and salinity fields with respective fields from the NOAA WOA13 atlas (Boyer et al., 2013). This atlas represents the last version of the NOAA temperature and salinity climatologies. For the upper 1500 m, the 1∕4^∘ resolution monthly WOA13 climatology was used, below this level we used the annual WOA13 temperature and salinity fields.

9.1 Temperature and salinity distributions at levels

As previously noted, the interpolation in WOA13 is performed on isobaric surfaces for temperature and salinity separately, so that similar difference patterns can be identified as in the case of isobarically and isopycnally averaged WAGHC climatologies. Indeed, Figs. 8a–f and 9a–f reveal several qualitatively similar patterns, indicating the largest differences in the areas with strong spatial gradients. We note that part of the differences should be attributed to climate change, since both climatologies are about 27 years apart on average. As progressive warming has been observed for the global ocean over the last few decades, Fig. 9a–f in contrast to Fig. 8a-f are dominated by the regions with positive temperature differences. These differences are described in more detail later in this paper. The introduction of the third term in Eq. (2) effectively reduces the depth bias near the boundaries, so that the differences in temperature and salinity in Fig. 8 are mostly due to the interpolation method.

The temperature and salinity differences between the isopycnal and isobaric versions of the WAGHC climatology at 150 m level for part of the northwestern Atlantic Ocean are shown in Fig. 10a and b. Here, along the path of the Gulf Stream, very high lateral temperature and salinity gradients occur with the effect of the data averaging method being especially pronounced. Parameter differences between the WAGHC and the WOA13 climatologies for the same level are presented in Fig. 10c and d. A very good agreement between the respective difference fields is clearly seen, suggesting that the differences between the WAGHC and WOA13 climatologies are mostly due to the difference in the interpolation method. Recently, the NCEI produced several regional climatologies including the Northwest Atlantic Regional Climatology (Seidov et al., 2016) with 0.1^∘ resolution. A comparison with this climatology might reduce the discrepancies but remains beyond the scope of the present study.

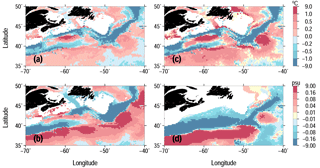
Figure 10Temperature (a) and salinity (b) differences between the isopycnally averaged and isobarically averaged WAGHC climatology in the northwestern Atlantic at the 150 m level in January; (c, d) same but for the isopycnally averaged WAGHC minus WOA13 differences.

Download

Figure 11T–S histograms for six depth layers of the world ocean. Bin sizes are 0.05 ^∘C for temperature and 0.005 for salinity. Histograms are based on the gridded WAGHC and WOA13 climatologies. Colors represent the volume fraction of each climatology.

Download

9.2 Differences in temperature–salinity space

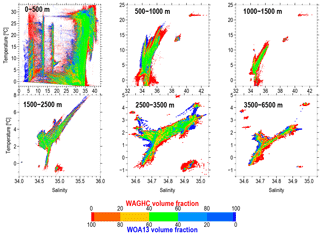
The differences between the WAGHC and the WOA13 atlas can be further identified using the volume T–S diagrams. For each bin the volume ratio $r=(V_{\mathrm{WOA}\mathrm{13}}-V_{\mathrm{WAGHC}})/(V_{\mathrm{WOA}\mathrm{13}}+V_{\mathrm{WAGHC}})$ was calculated giving the volume fraction represented by the WOA13 and WAGHC climatology, respectively. The T–S diagrams based on the gridded data for six selected depth layers are shown in Fig. 11. The largest differences between the two climatologies are found within the upper 1500 m layer, with the WOA13 usually showing broader T–S sequences compared to the WAGHC climatology. Unrealistically high WOA13 salinities exceeding 35.5 psu are found in the temperature range below 2 ^∘C. A generally good agreement is observed for the layers below 1500 m where the WOA13 climatology is represented by the annual temperature and salinity fields.

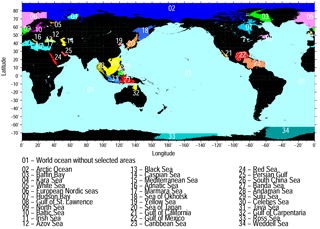
Figure 12Selected areas within the world ocean for which T–S histograms have been compared between the WAGHC and WOA13 climatologies. Please note that the above figure contains disputed territories.

Download

To permit a more detailed comparison of the thermohaline properties for both climatologies, we selected 34 regions within the world ocean (Fig. 12). In the following we describe the most pronounced differences revealed by the T–S diagrams for particular areas (Fig. 13a and b). Unfortunately, it is not possible to give a definite explanation for these differences, as many details regarding the construction of the WOA13 are not known to us. For the Arctic Ocean without the marginal seas, the WOA13 climatology produces unrealistically high salinities exceeding 36 psu. In contrast, for Baffin Bay, the Kara Sea, the White Sea and the European Nordic seas, WOA13 gives much lower salinities compared to the WAGHC climatology. For temperatures below ca. 2 ^∘C, the WOA13 climatology gives unrealistically high salinities for the Kara Sea, the White Sea, and Hudson Bay. At least part of the differences described above can be attributed to the much poorer WOA13 data basis for the northern polar region compared to the WAGHC.

Significantly different T–S diagrams are also found for several of the data abundant regions. For instance the Baltic Sea is characterized by extraordinarily good data coverage. However, significant deviations between the two climatologies are clearly seen: (1) the waters with salinities below 5 psu are completely absent in the WOA13; and (2) salinities higher than 25 psu are not known for the Baltic Sea but are present in the WOA13 climatology. Very different T–S diagrams are found for the Caspian Sea. Here, the WOA13 gridded fields report salinities lower than 7 psu throughout the whole temperature range, along with unrealistically high temperatures exceeding 30 ^∘C. For the Mediterranean Sea the WOA13 gridded product exhibits low-salinity sequences (below 36.5 psu) that are not supported by the observational data. In the Pacific Ocean we note the unrealistically broad WAGHC salinity range for the Sea of Okhotsk, especially for the deep waters with temperatures below 5 ^∘C. The T–S diagrams for the two climatologies differ considerably for the Gulf of California. Here the WOA13 climatology exhibits a very broad salinity range even for the deep part of the water column, with temperatures below 12 ^∘C where the T–S relation becomes very tight. Similar to the Gulf of California, we find WOA13 salinity ranges that are too broad in the deep waters of the Gulf of Mexico and the Caribbean Sea. The WOA13 climatology is also biased to low upper layer salinities in the Andaman and Java seas. Finally, we note a broader WOA13 salinity range for the Weddell Sea. Here, the WOA13 climatology gives unrealistically high salinities exceeding 35 psu, in disagreement with observations.

9.3 Volume-averaged temperature and salinity differences

As noted above, the spatial patterns of temperature and salinity differences at selected levels between the isopycnally averaged WAGHC climatology and isobarically averaged WOA13 climatology resemble the differences between the isopycnally and isobarically averaged WAGHC climatologies, suggesting the dependence on interpolation method.

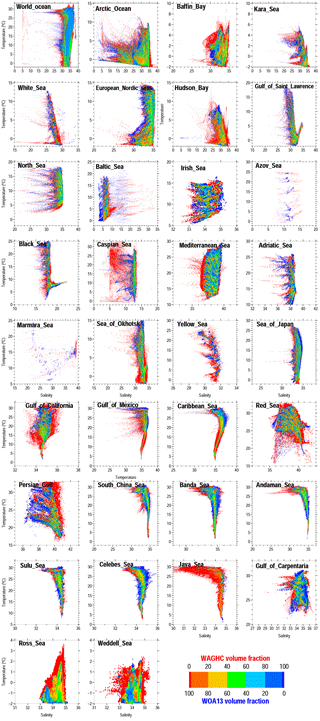
Figure 13T–S histograms for selected areas of the world ocean (see Fig. 12) for WAGHC and WOA13 gridded climatologies. Bin size is 0.1 ^∘C × 0.05 psu. Colors represent the volume fraction of each climatology. Please note that the above figure contains disputed territories.

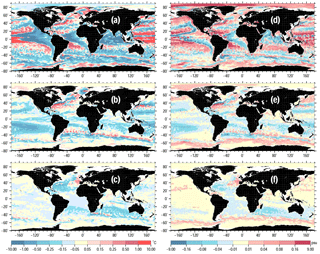
The zonally averaged temperature and salinity differences between the isobarically averaged WAGHC and WOA13 climatology are shown in Fig. 14. Using the isobarically averaged WAGHC, we tried to minimize the effect of isopycnal averaging. Both temperature and salinity sections show the WAGHC climatology as being warmer and saltier on average. A rather pronounced dependence on latitude is observed, with “tounges” of positive differences linked to the Antarctic Circumpolar Current and to latitudes north of 30^∘ N.

The mean temperature difference for the  0–300, 0–700, and 0–1500 m layers are 0.127, 0.079, and 0.048 ^∘C, respectively. We attribute these differences to real changes in the world ocean over an approximate 25-year time period between the WAGHC and WOA13 climatologies. The time difference plot (Figs. 14c and 15c) was produced assuming  1984 as the median year for the WOA13 climatology, which was created as the average of six decadal climatologies.

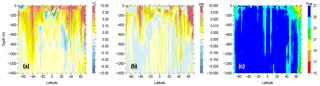
Figure 14Zonally averaged differences between the WAGHC and WOA13 climatologies for temperature (a), salinity (b), and mean climatological year (c).

Download

Figure 15Differences between the WAGHC and WOA13 climatologies vs. depth for temperature (a), salinity (b), and for the mean climatological year (c).

Download

9.5 Ocean heat content time series

Finally, we used the WAGHC and WOA13 climatologies to test them as the baseline mean for the calculations of the ocean heat content anomaly (OHCA) time series.

Here the OHCA time series between 1920 and 2016 (Fig. 18) were calculated as follows. First, the depth averaged temperatures for the 0–300 and 0–700 m layers were obtained. The mean layer temperature anomaly was then differenced from a baseline climatological monthly mean. The global temperature anomaly for each layer was represented as the area-weighted mean of all 1^∘ latitude zones containing data. For each 1^∘ zone, the temperature anomaly was represented by the mean of all 1^∘ boxes containing data. The calculated global temperature anomalies were converted to OHCA over the entire ocean area. This was equivalent to the assumption that the mean temperature anomaly for the ocean boxes without data was equal to the mean anomaly estimated for the grid boxes with observations. We note that the time series presented in Fig. 18 represent the decadal mean anomalies centered on each calendar year. Figure 18c–i shows temperature anomalies averaged for selected decades in 1×1^∘ boxes.

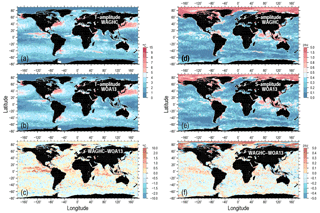
Figure 16Annual cycle amplitudes for temperature (a – WAGHC, b – WOA13) and salinity (d – WAGHC, e – WOA13) averaged over the upper 100 m layer for the WAGHC and WOA13 climatologies. Amplitude difference WAGHC minus WOA13 for temperature (c) and salinity (f).

Download

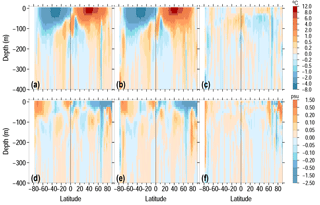
Figure 17Zonally averaged September minus March differences vs. depth for (a) WAGHC temperature, (b) WOA13 temperature; (c) difference a−b; (d) WAGHC salinity; (e) WOA13 salinity; and (f) difference d−e.

Download

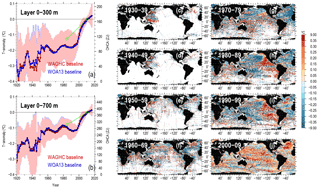
Figure 18Decadal globally integrated ocean heat content anomaly (ZJ) time series for 1920–2016 for 0–300 m (a) and 0–700 m (b) layers computed using WAGHC (red curve) and WOA13 (blue curve) baseline climatologies. Error bars correspond to the errors due to the irregular and incomplete sampling; the green line corresponds to the heat content change estimated by differencing the WAGHC and WOA13 climatologies. (c–j) The 0–300 m layer temperature anomalies in 1×1^∘ boxes averaged over the selected decades.

Download

The irregular data sampling is the largest source of uncertainty in global OHCA calculations. In order to estimate this kind of uncertainty, we used the global GECCO ocean synthesis (German contribution to Estimating the Circulation and Climate of the Ocean) (Köhl and Stammer, 2008). This method was previously applied to the upper-ocean temperature anomaly calculations (Gouretski et al., 2012). The GECCO synthesis provides an estimate of ocean circulation consistent with the dynamics of an ocean general circulation model. The depth-averaged decadal temperature time series for the 0–300 and 0–700 m layers were calculated from GECCO output (1) using boxes sampled in the historical record during each particular decade and (2) using the full model output. The standard deviation of the difference between the two time series provides the measure of uncertainty due to the irregular and incomplete sampling for that decade.

Unfortunately, the historical climatologies are based on data irregularly distributed in time and space and can have different mean years for different regions of the ocean, which introduces inconsistencies among the regions. Boyer et al. (2016) used three monthly mean temperature climatologies to test the sensitivity of the OHCA estimates for the global ocean to the choice of the baseline mean. The OHCA uncertainty for the 0–700 m layer due to the baseline mean was found to depend on the mapping method and time periods, varying between 2.7 and 24.5 ZJ, which corresponds to approximately 2 % to 16 % of the full OHCA range between 1970 and 2010.

Our calculations reveal much smaller differences due to the choice of baseline mean. The largest differences reach about 10 % of the full OHCA range for some years between 1920 and 2015 and are observed before the mid-1950s. This time period is characterized by an extremely uneven distribution of observations and almost no observations in the Southern Hemisphere, especially during the 1940s. After the mid-1950s, the differences due to the baseline mean do not exceed a few percent.

We find an OHCA increase of ∼150 ZJ since 1920 for the 0–300 m layer and of ∼220 ZJ for the 0–700 m layer. Both time series are characterized by an acceleration of the ocean heat content growth since the mid-1990s. As mentioned in Sect. 9.3, the WAGHC and WOA13 climatologies have a mean year difference exceeding 25 years, meaning that the overall temperature differences between the two climatologies can be attributed to climate change in the ocean over this time period. The overall temperature (OHCA) differences between the two climatologies are shown in green in Fig. 18, and in both cases they are lower than the OHCA differences obtained from decadal time series (72 % and 89 % for the 0–300 and 0–700 m layers, respectively).

The long-term data storage of the WAGHC climatology is provided by the Climate and Environmental Retrieval and Archive (CERA) system hosted and maintained by the German Climate Computing Center (DKRZ). The gridded climatology is available online at the Integrated Climate Data Center-ICDC, which is part of the Center for Earth System Research and Sustainability, (https://doi.org/10.1594/WDCC/WAGHC_V1.0; Gouretski, 2018).

The author declares that he has no conflict of interest.