the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Wind-induced variability in the Northern Current (northwestern Mediterranean Sea) as depicted by a multi-platform observing system
Maristella Berta
Lucio Bellomo
Annalisa Griffa
Marcello G. Magaldi
Anne Molcard
Carlo Mantovani
Gian Pietro Gasparini
Julien Marmain
Anna Vetrano
Laurent Béguery
Mireno Borghini
Yves Barbin
Joel Gaggelli
Céline Quentin
The variability and evolution of the Northern Current (NC) in the area off Toulon is studied for 2 weeks in December 2011 using data from a glider, a high-frequency (HF) radar network, vessel surveys, a weather station, and an atmospheric model. The NC variability is dominated by a synoptic response to wind events, even though the dataset also evidences early stages of transition from late summer to fall–winter conditions. With weak winds, the current is mostly zonal and in geostrophic balance even at the surface, with a zonal transport associated with the NC of ≈1 Sv. Strong westerly wind events (longer than 2–3 days) induce an interplay between the direct-wind-induced ageostrophic response and the geostrophic component: upwelling is observed, with offshore surface transport, surface cooling, flattening of the isopycnals, and reduced zonal geostrophic transport (0.5–0.7 Sv). The sea surface response to wind events, as observed by the HF radar, shows total currents rotated at to to the right of the wind. Performing a decomposition between geostrophic and ageostrophic components of the surface currents, the wind-driven ageostrophic component is found to rotate by to to the right of the wind. The ageostrophic component magnitude corresponds to ≈2 % of the wind speed.
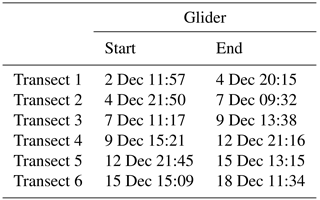
The Liguro–Provençal–Catalan Current, also called Northern Current (Millot, 1999), is a boundary current corresponding to the upper limb of the western Mediterranean circulation (Fig. 1a). It originates in the Ligurian Sea due to the convergence of the two currents flowing along each side of the Corsica island (Astraldi and Gasparini, 1992), namely the Western and Eastern Corsica currents (WCC and ECC). The Northern Current (denoted NC hereafter) flows southwestward along the continental slope of the Ligurian–Provençal and Balearic basins with a certain degree of continuity and may thus be recognized as a single entity as far as the Catalan Sea (Font et al., 1988; Garcia et al., 1994; Millot, 1987). Its importance mainly relies on the fact that all water masses in the area – namely the Modified Atlantic Water (MAW), the Levantine Intermediate Water (LIW) and the Western Mediterranean Deep Water (WMDW) – are carried by the current during its flowing (Conan and Millot, 1995). As a result, the NC is known to influence the coastal circulation of the Gulf of Lion (Duchez et al., 2012) and, most importantly, to modulate the supply of salt and/or heat by lateral advection in the convection areas (so-called preconditioning; see Schroeder et al., 2010) and thus to affect the important deep water formation process in the western Mediterranean. Also, the NC hugs the highly populated coasts of Italy and France, where areas of intense industrial development alternate with touristic and environmental relevant marine protected areas (MPAs). Understanding the flow dynamics and how it carries biological and pollutant quantities is of great importance for a correct management of coastal and marine activities.
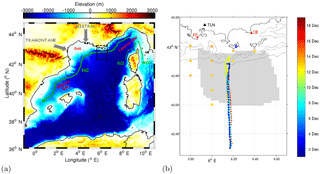
Figure 1(a) The western Mediterranean Sea, including northern circulation branches and main winds. The region of study is marked as a dashed black square. The following acronyms are used: GoL: Gulf of Lion, NC: Northern Current, WCC: Western Corsica Current, ECC: Eastern Corsica Current. (b) Details of the region of study including the synoptic measurements carried out during the experiment (2–19 December 2011). The gray area is the high-frequency (HF) radar surface current field coverage, while the two red crosses indicate the HF radar sites at Fort Peyras (FP) and Cap Bénat (CB), in the Toulon (TLN) area. The orange square marks represent the conductivity–temperature–depth (CTD) stations, while the dot array at 6.20∘ E shows the track of the repeated glider transects. CTD stations and glider tracks are color coded in time. The blue diamond indicates Porquerolles weather station's position. Bathymetric lines are at 500, 1000 and 2000 m depths.
The NC has been intensively observed in a few specific places on the southern French coast, namely (a) off Nice (Albérola et al., 1995a; Béthoux et al., 1982, 1988; Sammari et al., 1995; Taupier-Letage and Millot, 1986); (b) at the eastern edge of the Gulf of Lion, off Marseilles (Albérola and Millot, 2003; Conan and Millot, 1995; Flexas et al., 2002; Forget et al., 2008), and (c) along the Gulf of Lion shelf break (André et al., 2009; Lapouyade and de Madron, 2001; Petrenko, 2003; Rubio et al., 2009). All this past literature agrees on some of its large-scale characteristics: the NC is confined within approximately 35–40 km from the coast and has an average geostrophic transport value of about 1.8 Sv (1 Sv =106 m3 s−1) (Béthoux et al., 1982; Sammari et al., 1995). It exhibits a marked annual cycle: during winter, it gets stronger, closer to coast, narrowing (about 25 km) and deepening (about 450 m), while in summer, it weakens, extends more offshore increasing its width around 40 km, and gets thinner (about 250 m). Mesoscale activity also increases from late fall to winter and then it decreases in summer, and it is concentrated in two main time windows of 3–6 and 10–20 days, respectively (Albérola et al., 1995a; Millot, 1987; Sammari et al., 1995; Taupier-Letage and Millot, 1986).
Despite the numerous articles above, the study of the NC and its variability still represents an active area of research, especially at scales shorter than seasonal. Transport measurements provide a wide range of values in the literature, reaching minimum values of 0.5 Sv and showing significant variability in time (Conan and Millot, 1995) and in space (Petrenko, 2003). The reason for this variability within the annual cycle is not clear yet. It has been suggested that it may be due to different freshwater signals from precipitation and river runoff (Béthoux et al., 1988), to the WMDW formation process (Crépon and Boukthir, 1987), or inherited by the distinct behavior of the WCC and the ECC, whose annual peaks differ by several months (Astraldi and Gasparini, 1992).
In particular, the study of variability of the NC in the area off Toulon (between Nice and Marseilles) deserves particular attention for various reasons. The NC dynamics has been undersampled in the past and far less documented than in other regions such as off Nice and Marseille. Only recently the NC mesoscale meandering off Toulon has been specifically investigated through the comparison of models and observations (Guihou et al., 2013) and with data assimilation (Marmain et al., 2014). These studies indicate the role of prevailing northwesterly winds in the modulation of the NC circulation. In fact, the area near Toulon is peculiar because the mean NC circulation is resisted by the prevailing northwesterly winds in the area. The upwelling-prone winds can significantly alter the current, to the point that on some occasions they can stop its westward propagation and control its penetration in the Gulf of Lion (Millot and Wald, 1980). When this happens, a frontal zone separating warm NC waters and cold waters upwelled from the Gulf of Lion is established near the coast, and it has clearly been observed from satellite images (Millot and Wald, 1980).
In this paper, the variability of the NC in the area off Toulon is studied using results from a multi-platform experiment involving high-frequency (HF) radar, glider, a weather station, and a research vessel, carried out in the framework of the EU-MED project TOSCA (Tracking Oil Spills and Coastal Awareness network, http://www.tosca-med.eu, last access: 20 July 2018). The experiment took place during a period of approximately 2 weeks in December 2011 (2–19 December), characterized by intense westerly and northwesterly wind events. The wind response of coastal boundary currents such as the NC is complex, and based on the interplay between the direct ageostrophic response in the surface layers and the geostrophic modifications occurring along the whole water column. The response of boundary currents to winds has been studied by several authors using numerical model results, satellite, and in situ data (Aguiar et al., 2014; Magaldi et al., 2010; Schaeffer and Roughan, 2015). Experimental works are mostly based on a statistical approach, i.e., using long time series of wind and currents and computing correlations or identifying the main flow patterns corresponding to specific wind forcing (Kim et al., 2010; Kosro, 2005; Mihanović et al., 2011; Yuan et al., 2017).
Here, we focus on the dynamics of specific wind events, and take advantage of the multi-platform information, especially from HF radars for the surface and glider for the water column. Our general goal is to identify the main processes at work, and to investigate how to unravel the interplay between the direct-wind-induced surface response and the geostrophic response. The following two specific goals are pursued:
-
describing the sea current system evolution during the period of interest, quantifying the water column response to the wind in terms of isopycnal and zonal geostrophic velocity evolution; and
-
investigating the surface layer response to the wind, attempting a decomposition between geostrophic and ageostrophic components of the velocity.
The problem of decomposing the surface flow in geostrophic and ageostrophic components has been previously addressed in several works. Earlier works used hydrographic or acoustic Doppler current profiler (ADCP) information to infer the geostrophic flow (e.g., Chereskin and Roemmich, 1991; Weller et al., 1991; Wijffels et al., 1994), while more recently the global altimetric products (Lagerloef et al., 1999) have been used in several applications. Rio and Hernandez (2003) used Surface Velocity Program (SVP) drifters and altimetry to infer information at global scales, while HF radar results with altimetry have been used to compute wind-driven velocities in the Kuroshio Current (Tokeshi et al., 2007) and in the South Atlantic Bight (Yuan et al., 2017). However, for coastal boundary currents such as the NC and for the space and timescales we are interested in (tens of kilometers and days), the use of satellite altimetry requires special attention (Gómez-Enri et al., 2016; Vignudelli et al., 2000) and is often not appropriate because of problems of accuracy, land contamination, and low space and time resolution at least for global products (Berta et al., 2015; Bouffard et al., 2008).
In this paper, we investigate the use of glider data in conjunction with HF radar. There are several challenges in using glider transects, including limited space and time sampling (Piterbarg et al., 2014) and the fact that only one component of the geostrophic velocity can be retrieved. Here, we investigate how to best combine glider and HF radar data and in which flow conditions they can be best exploited.
The paper is organized as follows. In Sect. 2, the main questions addressed in the paper are stated, and the main definitions are introduced. In Sect. 3, a description of the data as well as the methods used to analyze them is provided. In Sect. 4, a description of the sea current system evolution over the whole water column is provided, while the analysis of the wind response in the surface layer is performed in Sect. 5. A summary and discussion are provided in Sect. 6.
As stated in the introduction, the general goal of this work is to investigate the variability of the NC during the period of interest, with special focus on the response of the system to wind forcing, using information from glider and HF radar. The velocity field of the system can always be written through kinematic decomposition as the superposition of a geostrophic and an ageostrophic component:
The geostrophic part, ug, obeys the balance between pressure gradient and Earth rotation (Coriolis). In the case of a boundary current, ug is expected to be driven by the large-scale pressure gradient of the general circulation, as well as by the more localized pressure gradient of mesoscale phenomena such as meanders and eddies (Centurioni et al., 2008; Gangopadhyay et al., 2013). The ageostrophic component, ua, includes the phenomena that are not in geostrophic balance. In the water column interior, we can expect that the flow is mostly geostrophic at scales longer than a day, while high-frequency processes such as internal waves, tides, or inertial oscillations play an important role at shorter timescales (Mensa et al., 2013).
At the surface, in addition to high-frequency processes, also ageostrophic processes related to direct wind and air–sea interaction are relevant. In particular, the surface velocity can be written as
where uSg is the surface geostrophic velocity, uSaW is the directly wind-driven component, and uSR includes all the other high-frequency processes such as tides, inertial and submesoscale variability, that for the purpose of this paper we will refer to as “residual”.
The wind response uSaW has been studied for many decades, starting from the pioneering work by Ekman (1905), considering idealized solutions of the balance between Coriolis and friction. The classic Ekman solution, valid in stationary and homogeneous conditions of infinite domain in the horizontal and at depth, is characterized by a surface current at 45∘ to the right of the wind (in the Northern Hemisphere) spiraling with depth in the surface layer. The solution is highly dependent on the specific parameterization of wind stress and vertical diffusivity. As an example, assuming that the wind stress linearly decreases with depth, this leads to the “slab” solution, which is 90∘ to the right of the wind and constant with depth (Pollard and Millard, 1970). The choice of other parameterizations as well as the presence of boundaries, finite depth, time dependence, and inhomogeneity further modifies the solution (Crise et al., 2006; Endoh and Nitta, 1971; Ralph and Niiler, 1999). Also, it can be expected that the simplified balance of the Ekman equation only partially captures the dynamics in realistic conditions, because of the interactions between the various processes. Indeed, direct measurements show a great range of variability in the observed wind response (Rio and Hernandez, 2003; Sentchev et al., 2017). In summary, even though the idealized solutions provide very important general guidance, the actual surface response to the wind in realistic conditions is still an open question (Stanichny et al., 2016), and it can be expected to depend on the specific environmental conditions.
We notice that there is a well-known direct dynamical link between uSaW and the geostrophic velocity ug. In the case of a boundary current, when the wind induces cross-shore transport, the cross-shore pressure gradient can be modified provided that the wind acts for a sufficiently long timescale, TW (Whitney and Garvine, 2005). For the Northern Current, Piterbarg et al. (2014) estimated that for winds of the order of 10 m s−1 TW is of the order of 2.5–3 days. In the case of upwelling-prone winds, as is the case of the westerly winds considered here, the ageostrophic surface response causes offshore transport that is compensated by deep water coastal upwelling, modifying both the surface pressure gradient and the water column stratification estimated by the potential density anomaly σ(z). This, in turn, alters the along-shore geostrophic component of the flow. In addition to this main mechanism, the geostrophic response can be further modulated by several other mechanisms, such as nonlinear frontal wind response (Oguz et al., 2017), and interactions with mesoscale and submesoscale instabilities.
The work performed here has two specific goals:
-
The first goal is to describe the variability of the NC over the whole water column and investigate its relationship with wind forcing.
The full 3-D description of is clearly not available from our data, but the data from glider and HF radar provide a good first approximation of the sea current system. The radar data provide estimates of the 2-D surface velocities , while the glider data provide information on the interior flow in terms of stratification, , and zonal geostrophic velocity, , estimated along the cross-shore glider transect. In this part of the work, we concentrate on variability over timescales of 1 day or longer, in keeping with the use of glider transect data and geostrophic velocities. In particular, we investigate the response of the sea current system during intense westerly wind events and concentrate on the main mechanism between wind-induced surface transport and upwelling response. Other mechanisms such as nonlinear wind response and interaction with instabilities are not directly considered here because we do not have enough information to resolve the various aspects.
-
The second goal is to further investigate the wind response in the surface layer and test a method to estimate the induced ageostrophic component uSaW.
The high-frequency response of the surface velocity as provided by the radar is used as a basis for the analysis. The estimate of uSaW is performed during periods of high winds, when it can be assumed that this term is prevalent with respect to uSR in Eq. (2). Still, the difficulty lies in identifying a reliable estimate for to be subtracted from in Eq. (2). A simple method based on the combined analysis of glider and HF radar data is put forth, valid for specific dynamic regimes.
Here, we review the datasets used in this study and describe the main data treatments and analyses that have been carried out. The data spatial coverage is shown in Fig. 1b, while a timeline of the measurements is shown in Fig. 2a.
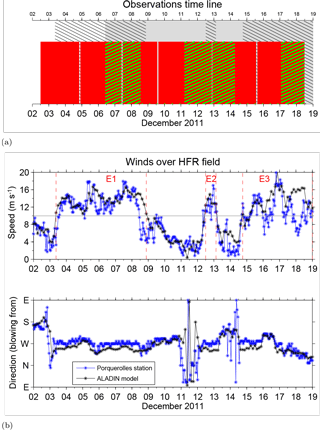
Figure 2(a) The multi-platform observations timeline: the black dashed lines indicate the selected wind events (compare with the panel below), the gray area indicates the radar dataset availability, the red areas indicate the glider transects, and the green dashed lines indicate the period in which the glider transects fall inside the HF radar coverage. (b) Wind time series from Porquerolles weather station (blue line) and from the ALADIN model (black line) are compared in terms of speed (middle panel) and direction (bottom panel). The limits of the selected wind events (speed >10 m s−1, gray line in the middle panel) are indicated with red dashed lines and named E1, E2, and E3.
3.1 Vessel-based measurements
During the experimental effort, an oceanographic cruise took place aboard the Italian R/V Urania between 10 and 15 December 2011. While measurements were performed within an extended offshore area between Nice and Toulon, here we consider only the Toulon measurements taken on 13 and 14 December. A total of 11 conductivity–temperature–depth (CTD) stations were sampled in the surrounding of the glider transect (Fig. 1b). The CTD data have been used for intercomparison and calibration of the glider hydrographic data as further discussed in Sect. 3.2–3.3.
3.2 Gliders
An autonomous underwater glider of the Slocum kind (Jones et al., 2005), manufactured by Webb Research Corporation, has been deployed and maintained operational during the period of 2–19 December (Fig. 2a). The glider, named Hannon, covered six repeated meridional transects off Toulon extending ∼70 km offshore (Fig. 1b). The onshore half of the transects laid within the HF radar coverage. The maximum profiling depth was set to 1000 m, giving mean horizontal distance between consecutive profiles, mean horizontal speed, and mean vertical speed of 1.7 km, 35 cm s−1, and 20 cm s−1, respectively. The timing details of each transect are summarized in the timeline in Fig. 2a and in Table 1.
Hannon was equipped with an unpumped SBE 41 CTD manufactured by Sea-Bird Electronics. CTD data were processed with dedicated Matlab routines taking care of all classic CTD response times and alignment issues, and all parameters were rebinned onto a regular vertical grid with a step of 2 dbar. Due to the use of an unpumped CTD and to the variable speed of the autonomous vehicle, the corrections were made speed-dependent using the glider speed computed through pressure variations and tilt angle. The thermal lag of the conductivity sensor was dealt also with speed-dependent coefficients (Morison et al., 1994) experimentally found through the technique proposed by Garau et al. (2011). The optimum values of the coefficients were αo=0.5447, αs=0.0708, τo=9.5117, and τs=7.69. Finally, temperature and conductivity values were post-calibrated against the Sea-Bird Electronics SBE 911+ CTD deployed from the R/V. For this purpose, only glider and ship profiles distant less than 14 km and separated by less than 12 h were considered, discarding all data shallower than 600 dbar.
3.3 Glider data analyses: isopycnal structure and computation of zonal geostrophic velocities
The glider hydrographic data were used to describe the NC current stratification and evolution. The hydrographic glider data have also been used to compute relative geostrophic velocities in the direction perpendicular to the glider transects, corresponding to the zonal direction. Potential density profiles were used, previously low-pass filtered through a Gaussian filter with 9 km cut-off wavelength. The Rossby radius was found through the dynamic mode decomposition of the average Brunt–Väisäla frequency profiles (Kundu et al., 1975). Although depth-averaged velocities from the glider could have been used to reference the geostrophic velocities, as done, e.g., by Davis et al. (2008), a calibration problem in Hannon's magnetic compass prevented us from doing so. Therefore, the velocities were referenced to a level of no motion z0, assumed to be in the range between 500–700 m. Sensitivity tests on z0 between 500 and 700 show very limited variability, with root mean square differences in the mean upper layer velocity of ≈2 %. In the following, results with z0=500 m are used.
The zonal geostrophic velocities were used also to compute the integrated transport, using the 5 cm s−1 isotach to identify the Northern Current, as done, e.g., by Albérola et al. (1995a) and Conan and Millot (1995).
3.4 HF radar
The HF radar (HFR) system has been operational during the period 6–19 December (Fig. 2a), covering the area in front of Toulon (Fig. 1b). The HF radar installation is based on the WERA technology (Gurgel et al., 1999) and relies on two systems. The first one (Fort Peyras, “FP” in Fig. 1b) has a quasi-monostatic configuration with an irregular, W-shaped eight-antenna receiving array and two monopoles performing the emission while forming a zero in the direction of the receiver. The peculiarity of the receiving array geometry is imposed by the environment of the site, a dismissed military base. The second system (Cap Bénat, “CB” in Fig. 1b) has a fully bistatic configuration, with the two monopoles in FP employed as emitter, and a regular linear eight-antenna array in CB operated as receiver (transmitter and receiver are 35 km apart).
The two systems operate at a frequency of 16.1 MHz with 50 kHz bandwidth, giving a nominal range resolution in the radial direction of 3 km. Antenna patterns are routinely measured almost every year and they had been applied to the December 2011 dataset. The azimuthal processing is done with the MUSIC (MUltiple SIgnal Characterization) direction-finding algorithm with a nominal 2∘ spacing (Lipa et al., 2006; Molcard et al., 2009; Sentchev et al., 2013), and radial velocity maps are produced every 20 min by integrating over the previous hour. Total velocity maps are then obtained on a regular 2 km grid through a local interpolation method which, at each grid point, minimizes the mean square error (MSE) between the projection of the total velocity onto the radial directions and the radial velocities available within a 3 km radius circle (Lipa and Barrick, 1983). Classically, total velocities are only computed when the angle between radial data from the two systems lies within the range 30–150∘, which corresponds to geometric dilution of precision (GDOP) values smaller than 2.5 (Chapman et al., 1997).
In our case, the requirement on the angle had to be reduced to 20–160∘ (corresponding approximately to GDOP values smaller than 4) in order to keep an acceptable offshore coverage on the region for the bistatic configuration. The Toulon radar system has been validated also during other TOSCA experiments involving the deployment of drifters, used to compare HF radar fields and derived velocities from in situ trajectories. Results show a high level of accuracy, on average 80 % agreement between drifters and HF radar, consistently using FP as quasi-monostatic configuration, CB as a different bistatic configuration (with emitter in Porquerolles, so that transmitter and receiver are 16 km apart), and GDOP values smaller than 2.5 (Bellomo et al., 2015; Berta et al., 2014).
HFR-measured velocities are the results of a vertical integration, through an exponential weighting function, over a characteristic depth λ0∕4π (Stewart and Joy, 1974), where λ0 is the resonant Bragg wavelength, which is half the wavelength of the emitted electromagnetic wave. For our systems, operating at a central frequency of 16.1 MHz, the characteristic depth is about 75 cm.
Due to the proximity of the FP site emitter with respect to the receiver array, imposed once again by the constraints of the military base, the HF radar coverage systematically experienced a drastic loss under strong Mistral winds. In fact, the wind-induced vibrations of the emitter antennas generated a phase noise in the receiver antennas' frequency spectrum, making in turn the signal-to-noise ratio unacceptably low at usually well-covered distances. Unfortunately, the problem was solved only after the observational campaign by placing the emitter farther outside the military base.
3.5 Analysis and interpretation of HF radar data
The HF radar fields are used to describe the evolution of the surface velocities. Preliminary tests have been performed using the raw data as well as low-pass-filtered data with a cut-off period of 36 h. Results, using raw and filtered data, agree within 86 % to 99 % in terms of average and rms velocities for v and u components, respectively, so that only results based on raw data are presented in the following.
We point out an important general issue regarding the interpretation of results based on HF radar velocities. Several papers (Ardhuin et al., 2009; Essen, 1993; Mao and Heron, 2008) have pointed out that the HFR-based surface velocity has, in addition to the actual Eulerian velocity , also a nonlinear wave correction (Weber and Barrick, 1977) that can be interpreted as a filtered surface Stokes drift, including the contribution of waves with wavelengths longer than the Bragg resonant wavelength.
A method to estimate this term has been proposed based on an accurate numerical wave model (Ardhuin et al., 2009). A debate is ongoing in the literature regarding the magnitude of the term and whether it is significant or not (Mao and Heron, 2008; Röhrs et al., 2015). An important factor is the fetch, since the longer the fetch, the more important the contribution of long waves (Essen et al., 2000). In our case, the Bragg resonant wavelength for our system is approximately 9 m, and the Stokes-like term cannot be explicitly estimated following Ardhuin et al. (2009) because we do not have access to the full wave spectrum information for the period of interest. Since the wind is predominantly from the west and northwest, and given the geography of the region (Fig. 1a), we can expect that the fetch is limited, and therefore the term is unlikely to be relevant. In absence of a quantitative estimate, though, we caution that the wind response term uSaW for our measurement could include not only the Ekman-type Eulerian response but also a possible Lagrangian contribution from Stokes drift. We will come back to this point in Sect. 5.
3.6 Wind data from weather station and atmospheric model
Hourly wind speed and direction measurements have been provided for the complete period of 2–19 December by Météo-France's Porquerolles station whose location is shown in Fig. 1b. In addition, Météo-France's ALADIN operational regional model ( and 3 h space and time resolution, respectively) has also been used.
Time series of wind speed and direction from the Météo-France station and from the model averaged over the area of interest (Fig. 1b) are shown in Fig. 2b. The results are qualitatively very similar, showing the good agreement of the model with the data and indicating that the wind patterns in the area are not characterized by strong gradients during the period of interest. Only during the last few days, after 18 December, the two time series show significant differences.
From the wind time series, events of high wind speed have been identified, considering a threshold of 10 m s−1. This choice is consistent with Mistral observations in the Toulon area, such as Caccia et al. (2004) and Guénard et al. (2005), and it is confirmed a posteriori by the consistency of the results as discussed in Sect. 5. As shown in Fig. 2a–b, the period of interest is characterized by two main events that last more than 3 days, E1 and E3, and a shorter event lasting less than 1 day, E2. The main wind direction is westerly and northwesterly, compatible with Mistral events in the area. We notice that E1 and E3 have duration longer than the estimated value of TW in the area (2–3 days) and therefore are likely to influence stratification and geostrophic velocity in the NC, as discussed in Sect. 2. The opposite holds for E2.
3.7 Summary of the measurements
In summary, the timeline of the main measurements carried out during the experiment is provided in Fig. 2a and includes
-
glider measurements (red boxes) covering the period of 2–19 December for a total of six transects, alternating offshore and inshore routes;
-
HF radar measurements (solid gray) starting 6 December, so that the first glider transect does not have contemporary HF radar data (the periods in which the glider transects fall inside the radar coverage are shown by green dashed lines); and
-
wind measurements and model outputs, which are available during the whole period of 2–19 December (the wind events E1, E2, and E3 are shown as dashed black lines).
In the following, the variability of the Northern Current is described during the period of interest (2–19 December). For simplicity, we partition the time of the analyses following the same time intervals as for the glider transects (Table 1, Fig. 2a). For each transect period, we provide a basic description based on the wind evolution together with the glider results on hydrography and zonal geostrophic velocity, and (when available) on the time-averaged surface velocity fields from HF radar. Radar velocity field averages are computed during periods in which the glider transects fall inside the radar coverage and considering only grid points with more than 80 % measurement coverage in time, in order to avoid mean flow contamination due to inhomogeneous coverages. For selected transects, all the information above from glider and HF radar is shown grouped together in a single multi-panel figure (Figs. 3–6).
Figure 3Potential temperature (a), salinity (b), and geostrophic velocity (c) for glider Transect 1 (see also Table 1 for time period definition). Potential density anomaly isolines (black) are in panels (a) and (b). The black dashed line (c) represents the southern boundary of the HF radar field.
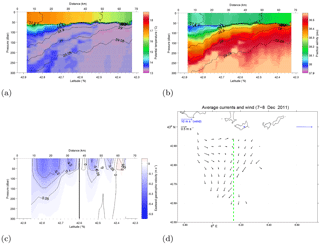
Figure 4Potential temperature (a), salinity (b), and geostrophic velocity (c) for glider Transect 3 (see also Table 1 for time period definition). Potential density anomaly isolines (black) are in panels (a) and (b). The black dashed line (c) represents the southern boundary of the HF radar field. In panel (d), black arrows show the surface currents from HFR averaged during the period in which the glider transect (green dashed line) falls inside the HFR coverage (and considering only grid points with at least 80 % available data over the time period). The blue arrow represents the wind from Porquerolles station averaged over the same period considered for the HFR average.
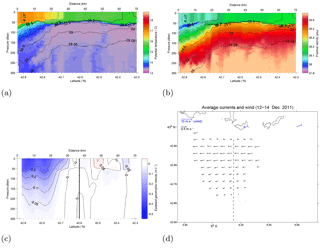
Figure 5Potential temperature (a), salinity (b), and geostrophic velocity (c) for glider Transect 5 (see also Table 1 for time period definition). Potential density anomaly isolines (black) are in panels (a) and (b). The black dashed line (c) represents the southern boundary of the HF radar field. In panel (d), black arrows show the surface currents from HFR averaged during the period in which the glider transect (green dashed line) falls inside the HFR coverage (and considering only grid points with at least 80 % available data over the time period). The blue arrow represents the wind from Porquerolles station averaged over the same period considered for the HFR average.
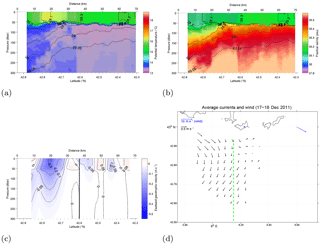
Figure 6Potential temperature (a), salinity (b), and geostrophic velocity (c) for glider Transect 6 (see also Table 1 for time period definition). Potential density anomaly isolines (black) are in panels (a) and (b). The black dashed line (c) represents the southern boundary of the HF radar field. In panel (d), black arrows show the surface currents from HFR averaged during the period in which the glider transect (green dashed line) falls inside the HFR coverage (and considering only grid points with at least 80 % available data over the time period). The blue arrow represents the wind from Porquerolles station averaged over the same period considered for the HFR average.
In order to quantify the flow variability, we show also some comprehensive figures that compare all transects in terms of the following metrics: evolution of the isopycnals σ(z) (Fig. 7), zonal geostrophic transport (Fig. 8), and comparison between surface zonal geostrophic velocity uSg estimated from the glider data and total surface velocity uS considering HF radar data along the glider tracks (Fig. 9).
Figure 7Potential density anomaly σ(z)=28.7 kg m−3 isopycnal evolution color coded for each glider transect.
4.1 Transect 1: initially calm condition followed by the onset of wind event E1
During Transect 1 (2–4 December), the glider moves offshore from the coast, and no HF radar data are available (see Fig. 2a). The wind speed (Fig. 2b) is initially weak, and then the first westerly event (E1) starts on 3 December. Notice that the period before the experiment (not shown) was characterized by calm conditions, with a week of weak winds, with speed smaller than 7.5 m s−1.
The hydrographic properties (potential temperature θ and practical salinity S) of Transect 1 are shown in Fig. 3a, b for the first 300 m, with overlying isolines of potential density anomaly σ(z). The transect plot origin of all hydrographic panels shown in the following figures is located a few kilometers off the coast (starting point of the glider mission). Following Boucher et al. (1987), we refer to the three zones that can be typically distinguished in the NC structure on the basis of the shape of the isopycnals with potential density anomaly σ in the range 28.7–29.05 kg m−3: the inshore flat part of the isopycnals defines the “coastal” (or marginal) zone, the sloping part identifies the “frontal” zone where the NC is most energetic, and the flat offshore part denotes the “central” basin zone. Here, we use σ=28.7 kg m−3 to characterize these zones (see also Fig. 7). The coastal marginal zone (typically flat) is not visible in the glider transect, while the frontal zone is evident and it extends up to N, i.e., at ≈40–45 km offshore. The θ and S transects (Fig. 3a, b) show a strong thermocline at 50 m in the offshore central region, accompanied by a salinity minimum (S<38 psu) right below the thermocline in the frontal zone. The fresher water centered around 80 m depth represents the core of the Modified Atlantic Water in the shallowest layer, laying over the Levantine Intermediate Water centered around a core with the highest salinity values (S>38.55 psu) and a relative temperature maximum. The presence of stratification with a strong thermocline at 50–100 m, together with the salinity minimum right below it, is typical of late summer conditions (Guibout, 1987, pp. 16 and 18 off Toulon and p. 36 off Nice, Albérola et al., 1995a) still present at the beginning of the experiment. The zonal geostrophic velocity ug computed along the transect shows a westward current extending up to 60 km off the coast with core (up to 0.4 m s−1 in first 100 m) located at ∼42.7–42.8∘ N (Fig. 3c). The offshore limit and depth of the NC are approximately ∼55 km and ∼175 m, respectively, with the core situated roughly at 25 km (Albérola et al., 1995a; Petrenko, 2003). The relatively large width and shallowness of the observed current here, known to be narrower and deeper than this during winter (Albérola et al., 1995a), confirm the presence of late-summer conditions at the beginning of the experiment.
4.2 Transects 2–3: wind event E1
During Transects 2 and 3 (4–7 and 7–9 December, respectively), while the glider travels back inshore and then offshore again, the wind is mostly dominated by the westerly event E1 (Fig. 2b), tapering off toward the end of the period. HF radar data are available starting from 6 December (Fig. 2a). The results of the two transects are qualitatively similar, so the complete results are shown only for Transect 3 in Fig. 4.
The hydrographic transects from the glider show a significant change with respect to Transect 1 (Fig. 3). Surface waters in the frontal zone are colder by ≈1.5 ∘C and the shape of the isopycnals is significantly flattened, while the mixed layer in the offshore central part is deepened by ≈20–30 m. This can be seen clearly also in Fig. 7, where the isopycnal with σ=28.7 kg m−3 is shown for all transects. Transects 2 and 3 show very similar isopycnal shape in the frontal area, flatter and shallower than for Transect 1. In the offshore central region, on the other hand, the isopycnal of Transect 2 is similar to the one of Transect 1, while for Transect 3 it deepens by ≈20–30 m. This is likely due to the different sampling times, since the glider covers the offshore region in Transect 3 about 2 days later than for Transect 2, and Transect 2 itself takes place shortly after the onset of E1 wind event (Fig. 2a).
The average surface velocity uS depicted by the HF radar during the glider sampling (Fig. 2a) is shown in Fig. 4d. Notice the reduced coverage with respect to the expected coverage (Fig. 1b), due to wind-induced interferences as discussed in Sect. 3.4. The velocity shows an overall offshore transport, with localized eastward reversals of the zonal current in the northwestern part of the radar coverage. The prevalent offshore current is consistent with the expected wind-driven transport to the right of the prevalent westerly wind (more in depth discussion is provided in Sect. 5).
Overall, the results suggest the presence of an upwelling phenomenon associated with the offshore transport induced by the westerly winds, that causes the flattening of the isopycnals in the frontal region and the cooling at the sea surface. In addition to the upwelling, other phenomena related to wind response are likely to occur, as suggested by the offshore isopycnal deepening in Figs. 4 and 7, due to mixing that deepens the thermocline and possibly to convection processes. Within the first 50–60 m depth of the zonal geostrophic velocity transect from the glider (Fig. 4c), we also observe recirculating cells further offshore the NC front associated with the wind-driven modification of the water masses' circulation offshore Toulon. This behavior is analogous to NC variability and meanders observations off Nice in fall–winter by Albérola et al. (1995a); Sammari et al. (1995). The recirculating cells are not visible in the surface current map because they lay outside the HFR field.
The zonal geostrophic velocity ug(y,z) computed from the glider is mostly westward but reduced with respect to Transect 1 (T1) in Fig. 3c, as expected during an upwelling episode. The difference between geostrophic velocity in T1 and T3, considering also the elapsed time between the two transects, is consistent with the estimate of the timescale TW (Whitney and Garvine, 2005) of 2–3 days needed for wind events to affect geostrophy in the NC (Piterbarg et al., 2014), and it suggests that E1 can modify stratification and geostrophic velocity after a sufficiently long wind forcing period.
The change in ug(y,z) is quantified computing the corresponding zonal transport (Fig. 8). For the integrated transport computation, the 5 cm s−1 isotach was used to identify the Northern Current, as done, e.g., by Albérola et al. (1995a) and Conan and Millot (1995). A very strong variability is seen with respect to the first transect, with the transport reduced by ≈50 % going from ≈1.15 Sv for T1 to 0.7–0.6 Sv for T2 and T3.
Finally, we provide a preliminary assessment of the surface deviation from geostrophy (that will be further investigated in Sect. 5) by comparing the magnitude of the zonal geostrophic velocity uSg from the glider with the total velocity uS depicted by the radar along the glider track (Fig. 9). During T2, the zonal radar total velocity is significantly lower than the geostrophic one, while the meridional component of the total velocity is almost double that of the zonal one. Results for T3 are qualitatively similar but incomplete because of the limited radar coverage. The observed magnitude difference in the zonal component from glider (geostrophic) and radar (total velocity) suggests that ageostrophic processes play a non-negligible role at the sea surface for T2–T3.
4.3 Transects 4–5: calm conditions interrupted by wind event E2 and onset of E3
Transects T4 and T5 (9–12 and 12–15 December, respectively) are characterized by mostly calm wind conditions (Fig. 2a), except for the brief westerly wind event (E2), occurring in between the two transects. Winds during the calm period are mostly westerly, except for some strong direction oscillations prevalent for lowest wind speed (below 4–5 m s−1), mostly evident in the Porquerolles station records. During the last day of T5, the onset of the third wind event (E3) occurs. Notice that E2 lasts less than a day, which is significantly less than TW estimated by Piterbarg et al. (2014), so that it is not expected to modify the stratification and geostrophic velocity structure even though of course it influences the surface velocity. The results of T4 and T5 are qualitatively similar, and the T5 results are shown in Fig. 5.
The hydrographic transects (Fig. 5a, b) indicate a narrowing and steepening of the frontal region characterized by warmer and fresher water in the surface layer. This is shown also by the σ isopycnals in Fig. 7 that are very similar for T4 and T5, and suggests a strong frontal area closer to the coast, approximately north of 42.7∘ N.
The zonal geostrophic velocity uSg (Fig. 5c) indeed shows a narrower but deeper and intensified current. The corresponding zonal geostrophic transport (Fig. 8) increases with respect to T2–T3, reaching values of ≈1–0.9 Sv for T4 and T5.
The radar surface velocity (Fig. 5d) is very different from the previous transects (Fig. 4d). The coverage is more extended and the velocity is almost completely zonal, showing the typical westward structure of the Northern Current. Notice that, even though the current actually deviates from the zonal direction during E2 (as further discussed in Sect. 5), the contribution to the average shown in Fig. 5d is very modest, because the average is performed during the glider sampling that overlaps only for a few hours with E2 (Fig. 2a). Also, E2 does not appear to significantly modify the stratification, the geostrophic velocity and the associated transport, as can be seen by the comparison of the two transects T4 and T5 in Figs. 7–8. This is in keeping with the fact that the duration of E2 is shorter than TW.
The surface comparison between geostrophic uSg and total velocity uS from HF radar shows an excellent agreement in the zonal direction for both T4 and T5 (Fig. 9c, d), while the meridional component in the frontal region is significantly lower than the zonal one (approximately 70 % and 85 % for T4 and T5, respectively). Overall, the results suggest that the current during these two transects is mostly zonal and geostrophic even at the surface, i.e., sustained by the large-scale pressure gradient that maintains the general and mesoscale circulation in the Ligurian basin.
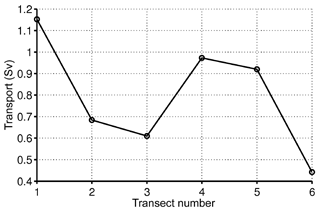
Figure 8Zonal transport computed from glider relative geostrophic velocity profiles (reference pressure at 500 mbar) for each glider transect.
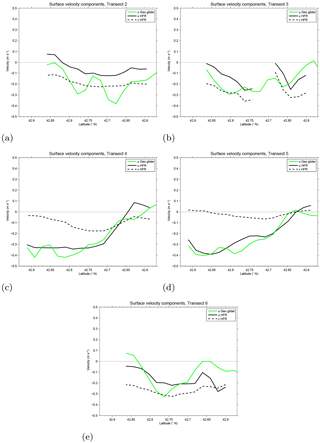
Figure 9Comparison of uS (solid black line) and vS (dashed black line) components of total surface currents from HFR and uSg (green line) geostrophic component from glider transects. Positive u(v) currents are eastward (northward), and the gray line indicates null velocities. Panels (a) to (e) represent measurements during Transects 2 to 6.
4.4 Transects 6: wind event E3
The last transect T6 (15–18 December) is dominated by the wind event E3, that is mostly westerly but veering toward northerly during the last day. The results are summarized in Fig. 6.
The hydrographic transects show a cooling of ≈1–1.5 ∘C in the frontal region, together with a strong flattening of the isopycnals as shown also in Fig. 7. The surface velocity depicted by the HF radar (Fig. 6d) is mostly meridional and offshore, in agreement with a wind response leading to upwelling. The geostrophic velocity is reduced (Fig. 6c), and the westward jet structure appears fragmented in several recirculation cells (as discussed for T2 and T3). The corresponding zonal geostrophic transport is reduced with respect to the previous transects, and is even lower than for T3 and T4, reaching values of ≈0.45 Sv (Fig. 8). The comparison between surface geostrophic uSg and radar-based total velocity uS (Fig. 9e) shows a significant deviation from geostrophy at the surface, as expected. uSg has a complex pattern, while uS is dominated by the meridional component (≈30 % bigger than the zonal velocities).
Overall, the results are qualitatively similar to the ones of T2 and T3, describing an upwelling response to the wind that influences and weakens the geostrophic circulation. It is interesting to notice, though, that there are also some differences in the hydrographic properties with respect to the previous transects that are likely to be related to the transition from late-summer to winter conditions. The salinity minimum present in the first transect (Fig. 3b) vanishes with time and it is almost absent in T6 (Fig. 6b), suggesting that the late summer conditions in T1 are turning toward a more typical winter configuration, probably due to the recurring effects of upwelling and mixing associated with the winter wind episodes. This is also shown by the pycnocline deepening by ≈30 m in the offshore central region (Fig. 7), occurring after the first two glider transects.
4.5 Summary of results
The main results from the above analysis can be summarized as follows.
-
The observed variability of the Northern Current during the experiment period is dominated by wind response. In addition to this synoptic variability, the overall hydrographic conditions also suggest early stages of transition from late summer to fall–winter conditions.
-
In absence of strong winds, the current is mostly zonal and geostrophic even at the sea surface. The associated zonal geostrophic transport over the water column is of the order of 1 Sv.
-
The response to strong westerly wind events (higher than 10 m s−1 and lasting more than 2–3 days) induces offshore meridional currents at the surface and an upwelling response in the water column that flattens isopycnals in the frontal region. The westward zonal geostrophic current is weakened, and the associated zonal transport decreases, up to 40–50 %, reaching values of ≈0.7–0.5 Sv.
-
A strong wind event lasting less than 1 day does not modify stratification and geostrophic velocity in the water column.
In Sect. 4, we have investigated the overall response of the NC to wind forcing, quantifying the variability of the water column stratification and of the zonal geostrophic transport. Here, we focus on the processes that regulate sea surface currents' response to direct wind forcing. Our final goal is to identify the ageostrophic wind-induced surface velocity uSaW, and characterize it in terms of amplitude and angle with respect to the wind.
The difficulty lies in the fact that the quantity that is actually measured by HF radar is the total surface velocity uS, rather than uSaW. This is a general problem in the study of surface wind response. Information on uS is provided by several instruments such as drifters, ADCP, or HF radar as in our case, and to decompose it in its various components (Eq. 2) is not an easy task (Rio and Hernandez, 2003). This is especially true in coastal studies where altimeter-based geostrophic velocities are not reliable. Often in experimental coastal studies, the surface velocity uS is correlated with the wind to investigate which percentage of the current variance can be explained or studied at different scales, in order to decompose various processes (Kim et al., 2010).
Here, we follow a two-step approach. As a first step, we consider the total velocity uS measured by the HF radars, in order to obtain some general information on the surface response to the westerly wind events. In particular, we investigate the time evolution of the angle between the current and the wind. As a second step, we isolate uSaW in selected periods, where we can provide an estimate of uSg based on the results of Sect. 4.
5.1 Investigation of the angle between wind and total surface velocity
Here, we characterize the wind response in terms of the angle between the wind and the total surface currents uS as measured by the radars. At each time interval of 1 h during the experiment period (Fig. 2a), the angle α between the radar surface currents and the ALADIN winds is computed for all the available radar grid points, interpolating the winds over the radar grid. At each time step, α is spatially averaged and time series of mean values and standard deviation (SD) are generated.
Results for the angle spatially averaged over the HFR field at each time step and SD(t) are shown in Fig. 10, with superimposed the time periods of the three wind events E1, E2, and E3 (Fig. 2). Positive (negative) values indicate currents to the left (right) of the wind. During all wind events, is significantly negative, except for a short period in 16 December, when a positive peak occurs. Notice though that the wind during that day dropped below the 10 m s−1 threshold (Fig. 2b). When the wind is low, i.e., outside the event periods, the angle oscillates between positive and negative values. Overall, the close response of the surface currents to the identified wind events provides a posteriori support to the choice of the 10 m s−1 wind speed threshold.
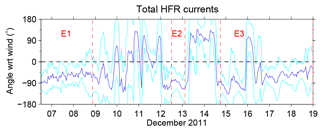
Figure 10Spatially averaged angle between total surface currents uS and average ALADIN winds over the HFR coverage (blue line). The black dashed line indicates a 0∘ angle. Negative angles indicate currents to the right of the wind direction. The cyan lines represent the SD. The limits of the selected wind events (E1, E2, and E3) are indicated with red dashed lines (see Fig. 2b for more details).
The results suggest a strong response of the total surface velocity to the wind events, with currents that tend to rotate to the right of the wind. The variability, quantified by the SD, is high, even though mostly confined to negative values. This indicates the presence of some inhomogeneity in the wind response, as already evident in the radar averages of Figs. 4, 6. These inhomogeneities can be due to many causes, from the configuration of the coast and/or the bathymetry (Kim et al., 2009), to the presence of mesoscale or submesoscale features, to inhomogeneities in the wind forcing over the radar coverage. Even though the ALADIN local wind is mostly homogeneous in the area of interest, wind gradients at larger spatial scales can also play a role in the surface currents' response (Lebeaupin Brossier and Drobinski, 2009).
The average values are for E1, for E2, and for E3. Since the wind is prevalently westerly (Fig. 2b), this suggests that the current is prevalently moving offshore, in agreement with the results in Sect. 4. Possible reasons for the differences between the three events will be further discussed in Sect. 5.3. The magnitude of the correlation between wind and total currents, as well as the phase angle between wind and currents, can also be estimated through the complex correlation method introduced by Kundu (1976). The phase angle estimated with this alternative method (not shown) is comparable, within the SD range, to the time series in Fig. 10. The average correlation magnitude between total currents and wind has values around 0.4 during the three wind events, which is reasonable given that total currents measured by HFR include the Ekman response to winds as well as other surface processes not directly wind related.
We notice that the angle between the total velocity and the wind is not directly indicative of wind response since uS contains also the geostrophic and ageostrophic residual components, and therefore cannot be compared with the angles predicted by the theoretical Ekman-like uSaW solutions. In the following, we will perform the decomposition of the geostrophic component from the HF radar total currents to estimate the magnitude and angle of uSaW.
5.2 Estimation of the geostrophic component and ageostrophic wind response
Here, we first of all assume that, during wind events, the ageostrophic velocity is dominated by the wind-induced component, i.e., uSaW≫uSR. This is partially justified by the fact that the uSR processes are mostly high frequency, and oscillations from tides are typically small in the area (Albérola et al., 1995b; Arabelos et al., 2011) while inertial oscillations are expected to be weaker during winter. Also, we recall that, as discussed in Sect. 3.5, we obtain consistent results using raw and 36 h low-pass-filtered HF radar data. The geostrophic component uSg, on the other hand, cannot be discarded since the results in Sect. 4 show that uSg remains a sizable part of uS in all cases (Fig. 9), even though its transport is reduced in presence of westerly wind events (Fig. 8).
As discussed above, performing the decomposition between ageostrophic and geostrophic components is challenging in most cases. In our case, we have information on the geostrophic velocity from the glider transects, but it is limited to the zonal direction and has restricted coverage in space and time. The results in Sect. 4, though, indicate that at least in some periods more extensive information can be obtained from the combination of glider and HF radar results.
During Transects 4–5, i.e., during the period 9–15 December when the wind was weak most of the time, the radar zonal velocity along the glider transect is very similar to the geostrophic one while the meridional velocity is reduced (Fig. 9c, d). The corresponding radar velocity field over the whole region (Fig. 5d) shows a well-defined zonal current with weak meridional dependence. These results justify an ansatz that, during periods of weak winds, the geostrophic surface field uSg can be approximated on the basis of the HF radar velocity appropriately averaged or filtered. We also assume that this estimate, indicated as , persists during wind episodes shorter than the timescale TW, i.e., for episodes of the order of 1 day. This is in agreement with the results in Sect. 4 regarding E2 (lasting less than 1 day) that suggest that the E2 winds do not significantly influence the stratification and the geostrophic velocity.
This ansatz is used to perform the decomposition and to study the wind response during E2. The geostrophic velocity is estimated averaging the radar velocity over a time period T prior to the onset of the wind event, and the ageostrophic wind response uSaW is estimated subtracting from the total radar velocity uS. A sensitivity study is carried out varying T in the range of 6–12 h, and the rms difference between the results is ≈20 % for .
An example of the geostrophic decomposition for a selected surface current field during E2, on 12 December at 14:00 LT, is shown in Fig. 11. The estimated field, considering the basic case of T=6 h for surface currents average, and the ALADIN wind are shown in Fig. 11a, c. The HF radar total velocity uS is shown in Fig. 11b, while the estimated uSaW, obtained subtracting the field in Fig. 11a from the field in Fig. 11b, is shown in Fig. 11d. Superimposed colors refer to the angle α of surface currents uSaW with respect to the wind. Subtracting the zonal westward geostrophic component from the total current field basically corresponds to rotating currents eastward and it results in decreasing the angle with respect to the westerly winds. The angle is negative for most of the field, except for a few grid points in the northeastern corner of the radar field.
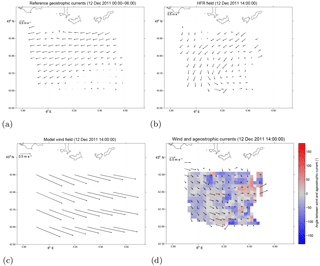
Figure 11Example maps of (a) 6 h time-averaged geostrophic flow uSg derived from HFR prior to the wind onset, (b) instaneous HFR surface currents uS during the wind event, (c) ALADIN wind field, and (d) ageostrophic surface currents uSaW superimposed on the color-coded map quantifying the angle α between the ageostrophic component and ALADIN wind. Negative values indicate current to the right of the wind.
Time series of spatially averaged results are shown in Fig. 12, for periods within E2 (left panels) and E3 (right panels) wind events. The estimated is characterized in terms of magnitude and angle with respect to the wind (Fig. 12a) averaged over all the radar grid points. Also, the percentage of negative angle values distributed over the radar field is shown in Fig. 12c, as an additional measure of variability. The angle between the wind and the ageostrophic component has a time average value , while the magnitude of the ageostrophic component reaches values of ≈25 cm s−1, comparable to the average magnitude of the geostrophic component and corresponding to the ≈2 % of the ALADIN wind average magnitude (about 13 m s−1). Negative angles, i.e., ageostrophic component to the right of the wind, prevail over the radar current field (up to about 80 % of all grid points) during the wind event (Fig. 12c).
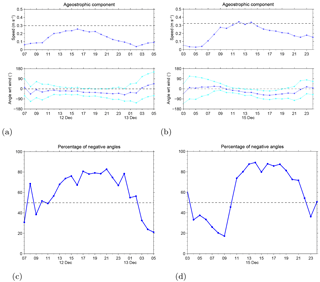
Figure 12(a, b) Time series of the spatially averaged ageostrophic component magnitude (top panels) and angle α(t) (middle panels) with respect to the wind direction (negative angle indicates currents to the right of the wind). The cyan lines in the bottom panels represent the SD. The black dashed lines in the top panels represent the average magnitude of the geostrophic component , while the black dashed lines in the middle panels indicate 0∘ angles. (c, d) Time series of the percentage of negative angles α (between ageostrophic component and wind) distributed over the HFR coverage. The black dashed lines in the bottom panels indicate 50 %.
The same method has also been applied to the onset of the wind event E3, considering only the first day of the wind episode, when we can assume that the estimate of the geostrophic velocity holds. Results in Fig. 12b show the angle between the wind and the ageostrophic component, with time average , while the ageostrophic component magnitude reaches values of ≈30 cm s−1, comparable to the average magnitude of the geostrophic component and corresponding to the ≈2.5 % of the ALADIN wind average magnitude (about 12 m s−1). Negative angles, i.e., ageostrophic component to the right of the wind, prevail over the radar current field (up to about 90 % of all grid points) during the wind event (Fig. 12d).
The surface current response to both wind events considered here shows similarities in terms of the angle between the ageostrophic component and the wind direction (about ) and also considering the magnitude of the ageostrophic component compared to wind speed (about 2 % as previously observed by Chang et al., 2012 and Poulain et al., 2009). Surface currents appear to respond to the wind quite homogeneously in space over the whole HF radar field.
5.3 Discussion
The results in Sect. 5.1–5.2 show that the average angle between the surface current and the wind is very different for the total surface current uS ( to ) and for the wind-driven ageostrophic component uSaW, ( to ). This highlights the importance of subtracting the geostrophic component of the velocity, especially in a boundary current situation where it is very relevant. The correction decreases the angle to the right of the wind, as it can be expected since the geostrophic velocity is primarily zonal and westward while the wind is mostly westerly.
More in detail, the different values of for uS during the three wind events (Fig. 10) can be due to a number of reasons. A first hypothesis is that they are linked to different values of the geostrophic velocity uSg. From the results in Sect. 4, uSg is expected to be stronger and more zonal during E2 and at the beginning of E1 and E3, i.e., when the wind has not yet acted to weaken it. This could explain the observed values of during those periods. As the time progresses during wind events E1 and E3, the zonal geostrophic velocity weakens, and as a consequence the angle is expected to decrease, as shown in Fig. 10. Another possible reason for the variability in values is the presence of time-varying inhomogeneities in the field, as suggested by the current reversals in Fig. 4, that could be due to, for instance, the interaction with the outflow from the Gulf of Lion (Schaeffer et al., 2011).
For uSaW, the values of are more similar in the two cases considered and the variability is reduced. It is interesting to compare these results with previous results in the literature, even though the comparison is challenging due to the use of different data and methods. A number of recent results are based on subtracting the geostrophic component estimated from altimetry data, and they consistently show angles to the right of the wind (in the Northern Hemisphere). Results from HF radar in the Kuroshio area (Tokeshi et al., 2007) suggest values of ≈38–48∘, while results from SVP drifters with drogue at 15 m (Rio and Hernandez, 2003) provide values of ≈10–40∘ at global scales for latitudes higher than 30∘ N. In the Black Sea, SVP drifter data (Stanichny et al., 2016) suggest values of ≈13∘ at the sea surface. Finally, in the Mediterranean Sea, Poulain et al. (2009) find from SVP and CODE drifters (drogued at 1 m) values of ≈27–42 and ≈17–20∘, respectively, obtained without subtracting the geostrophic component. Overall, these values suggest a range of ≈10–40∘, that is consistent with our results. With respect to our results, though, we notice that most of the previous results have been obtained considering a larger-scale geostrophic component and longer timescales of a few days. An exception is given by the work of Sentchev et al. (2017) in the Toulon area, that considers daily wind oscillations corresponding to light sea breeze. Results from HF radar and ADCP in this case suggest angles of ≈15–20∘ to the left of the wind, indicating a different balance with respect to the typical Ekman balance.
An important final remark is the fact that, as pointed out in Sect. 3, estimates of uSaW based on HF radars and surface drifters are likely to be at least partially biased by the Stokes drift-like component of the velocity (Ardhuin et al., 2009). This component is expected to be in the same direction as the wind, therefore causing a bias that tends to decrease the value of the estimated angle. In our case, then, the angle of the actual Eulerian velocity could exceed . This issue, that is common to all the works based on HF radar and surface drifters, is outside the scope of the present paper but it will be considered in future works, considering additional wave spectra information.
In this paper, a multi-platform observing system is used to monitor the variability of the boundary current of the northwestern Mediterranean Sea, i.e., the Northern Current. The adopted multi-platform system gives synoptic measurements of currents and water masses' properties at spatiotemporal scales that cannot be resolved only with classical vessel surveys or satellite remote sensing. We use water column data from repeated glider transects and vessel surveys, surface current fields from HF radar, wind time series from a weather station, and an atmospheric model to describe the evolution of the NC off Toulon for a period of approximately 2 weeks in December 2011.
The hydrographic transects display flattening of isopycnals and deepening of the mixed layer offshore, evidencing early stages of the transition from late summer to fall–winter typical conditions (Albérola et al., 1995a; Guibout, 1987). In addition, the NC variability is dominated by a synoptic response to wind events. When the wind is weak, the current is mostly zonal and in geostrophic balance even at the surface, with a zonal transport associated with the NC of ≈1 Sv. During two strong westerly wind events lasting longer than 2–3 days, an upwelling response is observed, with offshore surface transport, surface cooling, flattening of the isopycnals and reduced zonal geostrophic transport (0.5–0.7 Sv). When the wind lasts less than 1 day, surface currents respond to winds but the water column stratification and the geostrophic transport are not affected because the wind event is not persistent enough.
We also specifically investigate the surface currents' response to the wind. The total surface current as observed by the HF radar is found to respond to the wind events, rotating at to to the right of the wind. During the first day of selected wind events, we also perform a decomposition between geostrophic and ageostrophic components of the surface current using results from glider and HF radar. The directly wind-driven ageostrophic component is found to rotate by a smaller angle to to the right of the wind. The ageostrophic component magnitude corresponds to ≈2 % of the wind speed.
This paper provides a first step in the joint use of glider and HF radar data to describe the variability of a boundary current in terms of both geostrophic and ageostrophic processes. Results show a high synoptic variability of the geostrophic component related to wind episodes persistent enough to modify water column stratification and pressure gradients, pointing to the difficulties of decomposing flow dynamics according to timescales and forcings (Kim et al., 2010).
The decomposition in geostrophic and ageostrophic velocity was carried out for space and timescales smaller than in most previous works (Rio and Hernandez, 2003; Tokeshi et al., 2007), i.e., of the order of 1 day and tens of kilometers, as appropriate scales for the Northern Current. Further developments in the decomposition method are foreseen using time-dependent geostrophic velocities. This approach will be first tested using models results with an Observing System Simulation Experiment (OSSE) type of approach, and we expect that it will provide useful insights for data assimilation and data blending applications. Other methodologies involving other in situ data or remote sea surface temperature (SST) measurements (Essen, 1995) can also be foreseen for the identification of the geostrophic part of the flow.
A number of interesting issues, that are not considered here, will be considered in future works. They include nonlinear wind response in the frontal area, and interactions with mesoscale and submesoscale instabilities that can modulate the geostrophic and ageostrophic response. Also, the effects of the bias due to the Stokes-like term in the HF radar velocity retrievals need further investigation.
More generally, several multi-platform observing systems are recently developing as a transnational effort within the Mediterranean oceanographic community. These systems are making available unprecedented synoptic high-resolution datasets that could be combined not only for specific scientific purposes but also for practical applications such as the management of coastal and marine shared resources.
Data can be provided upon request to the authors.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Coastal marine infrastructure in support of monitoring, science, and policy strategies”. It is not associated with a conference.
The analysis of the dataset has been supported and co-financed by the
JERICO-NEXT project. This project has received funding from the European
Union's Horizon 2020 research and innovation program under grant agreement
no. 654410. The multi-platform experiment has been carried out within the
TOSCA project, co-funded by the European Regional Development Fund in the
framework of the MED program. Wind data were kindly made available by
Météo-France. The authors wish to thank R/V Urania's crew that
made the experiment possible, the glider support team of DT-INSU, and
MIO's HF radar team.
Edited by: Ingrid Puillat
Reviewed by: two anonymous referees
Aguiar, A., Cirano, M., Pereira, J., and Marta-Almeida, M.: Upwelling processes along a western boundary current in the Abrolhos-Campos region of Brazil, Cont. Shelf Res., 85, 42–59, https://doi.org/10.1016/j.csr.2014.04.013, 2014. a
Albérola, C. and Millot, C.: Circulation in the French mediterranean coastal zone near Marseilles: the influence of wind and the Northern Current, Cont. Shelf Res., 23, 587–610, 2003. a
Albérola, C., Millot, C., and Font, J.: On the seasonal and mesoscale variabilities of the Northern Current during the PRIMO-0 experiment in the western Mediterranean Sea, Oceanol. Acta, 18, 163–192, 1995a. a, b, c, d, e, f, g, h, i
Albérola, C., Rousseau, S., Millot, C., Astraldi, M., Font, J., Garcia-Lafuente, J., Gasparini, G.-P., Send, U., and Vangriesheim, A.: Tidal currents Western Mediterranean, Oceanol. Acta, 18, 273–284, 1995b. a
André, G., Garreau, P., and Fraunié, P.: Mesoscale slope current variability in the Gulf of Lions. Interpretation of in-situ measurements using a three-dimensional model, Cont. Shelf Res., 29, 407–423, 2009. a
Arabelos, D. N., Papazachariou, D. Z., Contadakis, M. E., and Spatalas, S. D.: A new tide model for the Mediterranean Sea based on altimetry and tide gauge assimilation, Ocean Sci., 7, 429–444, https://doi.org/10.5194/os-7-429-2011, 2011. a
Ardhuin, F., Marié, L., Rascle, N., Forget, P., and Roland, A.: Observation and Estimation of Lagrangian, Stokes, and Eulerian Currents Induced by Wind and Waves at the Sea Surface, J. Phys. Oceanogr., 39, 2820–2838, https://doi.org/10.1175/2009JPO4169.1, 2009. a, b, c, d
Astraldi, M. and Gasparini, G. P.: The seasonal characteristics of the circulation in the North Mediterranean Basin and their relationship with the atmospheric-climatic conditions, J. Geophys. Res., 97, 9531–9540, 1992. a, b
Bellomo, L., Griffa, A., Cosoli, S., Falco, P., Gerin, R., Iermano, I., Kalampokis, A., Kokkini, Z., Lana, A., Magaldi, M., Mamoutos, I., Mantovani, C., Marmain, J., Potiris, E., Sayol, J., Barbin, Y., Berta, M., Borghini, M., Bussani, A., Corgnati, L., Dagneaux, Q., Gaggelli, J., Guterman, P., Mallarino, D., Mazzoldi, A., Molcard, A., Orfila, A., Poulain, P.-M., Quentin, C., Tintoré, J., Uttieri, M., Vetrano, A., Zambianchi, E., and Zervakis, V.: Toward an integrated HF radar network in the Mediterranean Sea to improve search and rescue and oil spill response: the TOSCA project experience, J. Oper. Oceanography, 8, 95–107, https://doi.org/10.1080/1755876X.2015.1087184, 2015. a
Berta, M., Bellomo, L., Magaldi, M. G., Griffa, A., Molcard, A., Marmain, J., Borghini, M., and Taillandier, V.: Estimating Lagrangian transport blending drifters with HF radar data and models: Results from the TOSCA experiment in the Ligurian Current (North Western Mediterranean Sea), Prog. Oceanogr., 128, 15–29, https://doi.org/10.1016/j.pocean.2014.08.004, 2014. a
Berta, M., Griffa, A., Magaldi, M. G., Özgökmen, T. M., Poje, A. C., Haza, A. C., and Olascoaga, M. J.: Improved surface velocity and trajectory estimates in the Gulf of Mexico from blended satellite altimetry and drifter data, J. Atmos. Ocean. Tech., 32, 1880–1901, https://doi.org/10.1175/JTECH-D-14-00226.1, 2015. a
Béthoux, J. P., Prieur, L., and Nyffeler, F.: The water circulation in the north-western Mediterranean Sea, its relations with wind and atmospheric pressure, 129–142, Elsevier Scientific Publishing Company, 1982. a, b
Béthoux, J.-P., Prieur, L., and Bong, J.-H.: Le courant Ligure au large de Nice, Oceanol. Acta, SP, H. J. Minas and P. Nival, 59–67, 1988. a, b
Boucher, J., Ibanez, F., and Prieur, L.: Daily and seasonal variations in the spatial distribution of zooplankton populations in relation to the physical structure in the Ligurian Sea Front, J. Mar. Res., 45, 133–173, 1987. a
Bouffard, J., Vignudelli, S., Cipollini, P., and Menard, Y.: Exploiting the potential of an improved multimission altimetric data set over the coastal ocean, Geophys. Res. Lett., 35, L10601, https://doi.org/10.1029/2008GL033488, 2008. a
Caccia, J.-L., Guénard, V., Benech, B., Campistron, B., and Drobinski, P.: Vertical velocity and turbulence aspects during Mistral events as observed by UHF wind profilers, Ann. Geophys., 22, 3927–3936, https://doi.org/10.5194/angeo-22-3927-2004, 2004. a
Centurioni, L. R., Ohlmann, J. C., and Niiler, P. P.: Permanent Meanders in the California Current System, J. Phys. Oceanogr., 38, 1690–1710, https://doi.org/10.1175/2008JPO3746.1, 2008. a
Chang, Y.-C., Chen, G.-Y., Tseng, R.-S., Centurioni, L. R., and Chu, P. C.: Observed near-surface currents under high wind speeds, J. Geophys. Res.-Oceans, 117, c11026, https://doi.org/10.1029/2012JC007996, 2012. a
Chapman, R. D., Shay, L. K., Graber, H. C., Edson, J. B., Karachintsev, A., Trump, C. L., and Ross, D. B.: On the accuracy of HF radar surface current measurements: Intercomparisons with ship-based sensors, J. Geophys. Res., 102, 18737–18748, 1997. a
Chereskin, T. K. and Roemmich, D.: A Comparison of Measured and Wind-derived Ekman Transport at 11∘N in the Atlantic Ocean, J. Phys. Oceanogr., 21, 869–878, https://doi.org/10.1175/1520-0485(1991)021<0869:ACOMAW>2.0.CO;2, 1991. a
Conan, P. and Millot, C.: Variability of the Northern Current off Marseilles, Western Mediterranean Sea, from February to June 1992, Oceanol. Acta, 18, 193–205, 1995. a, b, c, d, e
Crépon, M. and Boukthir, M.: Effect of deep water formation on the circulation of the Ligurian Sea, Ann. Geophys., 5B, 43–48, 1987. a
Crise, A., Querin, S., and Malačič, V.: A strong Bora event in the Gulf of Trieste: a numerical study of wind driven circulation in stratified conditions with a preoperational model, Acta Adriat., Supplement, 47, 185–206, 2006. a
Davis, R. E., Ohman, M. D., Rudnick, D. L., and Sherman, J. T.: Glider surveillance of physics and biology in the southern California Current System, Limnol. Oceanogr., 53, 2151–2168, 2008. a
Duchez, A., Verron, J., Brankart, J.-M., Ourmières, Y., and Fraunié, P.: Monitoring the Northern Current in the Gulf of Lions with an observing system simulation experiment, Sci. Mar., 76, 441–453, 2012. a
Ekman, V. W.: On the influence of the Earth's rotation on ocean-currents., Arkiv for Matematik, Astronomi, och Fysik, 2, 1–52, 1905. a
Endoh, M. and Nitta, T.: A Theory of Non-Stationary Oceanic Ekman Layer, J. Meteorol. Soc. Jpn., 49, 261–266, https://doi.org/10.2151/jmsj1965.49.4_261, 1971. a
Essen, H.-H.: Ekman portion of surface currents, as measured by radar in different areas, Deutsche Hydrografische Zeitschrift, 45, 57–85, https://doi.org/10.1007/BF02226315, 1993. a
Essen, H.-H.: Geostrophic surface currents as derived from satellite SST images and measured by a land-based HF radar, Int. J. Remote Sens., 16, 239–256, https://doi.org/10.1080/01431169508954393, 1995. a
Essen, H. H., Gurgel, K. W., and Schlick, T.: On the accuracy of current measurements by means of HF radar, IEEE J. Oceanic. Eng., 25, 472–480, https://doi.org/10.1109/48.895354, 2000. a
Flexas, M. M., de Madron, X. D., Garcia, M. A., Canals, M., and Arnau, P.: Flow variability in the Gulf of Lions during the MATER HFF experiment (March–May 1997), J. Marine Syst., 33–34, 197–214, 2002. a
Font, J., Salat, J., and Tintoré, J.: Permanent features of the general circulation in the Catalan Sea, Oceanol. Acta, 9, 51–57, 1988. a
Forget, P., Barbin, Y., and André, G.: Monitoring of surface ocean circulation in the Gulf of Lions (North-West Mediterranean Sea) using WERA HF radars, in: IGARSS 2008, Boston, USA, 2008. a
Gangopadhyay, A., Bharat Raj, G. N., Chaudhuri, A. H., Babu, M. T., and Sengupta, D.: On the nature of meandering of the springtime western boundary current in the Bay of Bengal, Geophys. Res. Lett., 40, 2188–2193, https://doi.org/10.1002/grl.50412, 2013. a
Garau, B., Ruiz, S., Zhang, W. G., Pascual, A., Heslop, E., Kerfoot, J., and Tintoré, J.: Thermal Lag Correction on Slocum CTD Glider Data, J. Atmos. Ocean. Tech., 28, 1065–1071, 2011. a
Garcia, M. J. L., Millot, C., Font, J., and Garcia-Ladona, E.: Surface circulation variability in the Balearic Basin, J. Geophys. Res.-Oceans, 99, 3285–3296, https://doi.org/10.1029/93JC02114, 1994. a
Gómez-Enri, J., Cipollini, P., Passaro, M., Vignudelli, S., Tejedor, B., and Coca, J.: Coastal Altimetry Products in the Strait of Gibraltar, IEEE T. Geosci. Remote, 54, 5455–5466, https://doi.org/10.1109/TGRS.2016.2565472, 2016. a
Guénard, V., Drobinski, P., Caccia, J.-L., Campistron, B., and Bench, B.: An Observational Study of the Mesoscale Mistral Dynamics, Bound.-Lay. Meteorol., 115, 263–288, https://doi.org/10.1007/s10546-004-3406-z, 2005. a
Guibout, P.: Atlas Hydrologique de la Méditerranée, Laboratoire d'Océanographie Physique du Museum National d'Histoire Naturelle, edited by: FREMER, Paris – SHOM, 1 vol., XV-150 pp., 1987. a, b
Guihou, K., Marmain, J., Ourmières, Y., Molcard, A., Zakardjian, B., and Forget, P.: A case study of the mesoscale dynamics in the North-Western Mediterranean Sea: a combined data-model approach, Ocean Dynam., 63, 793–808, https://doi.org/10.1007/s10236-013-0619-z, 2013. a
Gurgel, K.-W., Antonischki, G., Essen, H.-H., and Schlick, T.: Wellen Radar (WERA): a new ground-wave HF radar for ocean remote sensing, Coast. Eng., 37, 219–234, 1999. a
Jones, C., Creed, E., Glenn, S., Kerfoot, J., Kohut, J., Mudgal, C., and Schofield, O.: Slocum gliders – A component of operational oceanography, in: Proc. 14th Int. Symp. on Unmanned Untethered Submersible Technology, Lee, NH, Autonomous Undersea Systems Institute, 2005. a
Kim, S. Y., Cornuelle, B. D., and Terrill, E. J.: Anisotropic Response of Surface Currents to the Wind in a Coastal Region, J. Phys. Oceanogr., 39, 1512–1533, https://doi.org/10.1175/2009JPO4013.1, 2009. a
Kim, S. Y., Cornuelle, B. D., and Terrill, E. J.: Decomposing observations of high-frequency radar-derived surface currents by their forcing mechanisms: Locally wind-driven surface currents, J. Geophys. Res.-Oceans, 115, c12046, https://doi.org/10.1029/2010JC006223, 2010. a, b, c
Kosro, P. M.: On the spatial structure of coastal circulation off Newport, Oregon, during spring and summer 2001 in a region of varying shelf width, J. Geophys. Res.-Oceans, 110, c10S06, https://doi.org/10.1029/2004JC002769, 2005. a
Kundu, P. K.: Ekman Veering Observed near the Ocean Bottom, J. Phys. Oceanogr., 6, 238–242, https://doi.org/10.1175/1520-0485(1976)006<0238:EVONTO>2.0.CO;2, 1976. a
Kundu, P. K., Allen, J. S., and Smith, R. L.: Modal decomposition of the velocity field near the Oregon coast, J. Phys. Oceanogr., 5, 683–704, 1975. a
Lagerloef, G. S. E., Mitchum, G. T., Lukas, R. B., and Niiler, P. P.: Tropical Pacific near-surface currents estimated from altimeter, wind, and drifter data, J. Geophys. Res.-Oceans, 104, 23313–23326, https://doi.org/10.1029/1999JC900197, 1999. a
Lapouyade, A. and de Madron, X. D.: Seasonal variability of the advective transport of particulate matter and organic carbon in the Gulf of Lion (NW Mediterranean), Oceanol. Acta, 24, 295–312, 2001. a
Lebeaupin Brossier, C. and Drobinski, P.: Numerical high-resolution air-sea coupling over the Gulf of Lions during two tramontane/mistral events, J. Geophys. Res.-Atmos., 114, d10110, https://doi.org/10.1029/2008JD011601, 2009. a
Lipa, B., Nyden, B., Ullman, D. S., and Terrill, E.: SeaSonde Radial Velocities: Derivation and Internal Consistency, IEEE J. Ocean. Eng., 31, 850–861, 2006. a
Lipa, B. J. and Barrick, D. E.: Least-Squares Methods for the Extraction of Surface Currents from CODAR Crossed-Loop Data: Application at ARSLOE, IEEE J. Ocean. Eng., OE-8, 226–253, 1983. a
Magaldi, M. G., Özgökmen, T. M., Griffa, A., and Rixen, M.: On the response of a turbulent coastal buoyant current to wind events: the case of the Western Adriatic Current, Ocean Dynam., 60, 93–122, 2010. a
Mao, Y. and Heron, M. L.: The Influence of Fetch on the Response of Surface Currents to Wind Studied by HF Ocean Surface Radar, J. Phys. Oceanogr., 38, 1107–1121, https://doi.org/10.1175/2007JPO3709.1, 2008. a, b
Marmain, J., Molcard, A., Forget, P., Barth, A., and Ourmières, Y.: Assimilation of HF radar surface currents to optimize forcing in the northwestern Mediterranean Sea, Nonlin. Processes Geophys., 21, 659–675, https://doi.org/10.5194/npg-21-659-2014, 2014. a
Mensa, J. A., Garraffo, Z., Griffa, A., Özgökmen, T. M., Haza, A., and Veneziani, M.: Seasonality of the submesoscale dynamics in the Gulf Stream region, Ocean Dynam., 63, 923–941, https://doi.org/10.1007/s10236-013-0633-1, 2013. a
Mihanović, H., Cosoli, S., Vilibić, I., Ivanković, D., Dadić, V., and Gačić, M.: Surface current patterns in the northern Adriatic extracted from high-frequency radar data using self-organizing map analysis, J. Geophys. Res.-Oceans, 116, c08033, https://doi.org/10.1029/2011JC007104, 2011. a
Millot, C.: Circulation in the Western Mediterranean Sea, Oceanol. Acta, 10, 143–148, 1987. a, b
Millot, C.: Circulation in the Western Mediterranean Sea, J. Marine Syst., 20, 423–442, 1999. a
Millot, C. and Wald, L.: The effect of Mistral wind on the Ligurian current near Provence, Oceanol. Acta, 3, 399–402, 1980. a, b
Molcard, A., Poulain, P. M., Forget, P., Griffa, A., Barbin, Y., Gaggelli, J., Maistre, J. C. D., and Rixen, M.: Comparison between VHF radar observations and data from drifter clusters in the Gulf of La Spezia (Mediterranean Sea), J. Marine Syst., 78, S79–S89, 2009. a
Morison, J., Andersen, R., Larson, N., D'Asaro, E., and Boyd, T.: The Correction for Thermal-Lag Effects in Sea-Bird CTD Data, J. Atmos. Ocean. Tech., 11, 1151–1164, 1994. a
Oguz, T., Mourre, B., and Tintoré, J.: Modulation of frontogenetic plankton production along a meandering jet by zonal wind forcing: An application to the Alboran Sea, J. Geophys. Res.-Oceans, 122, 6594–6610, https://doi.org/10.1002/2017JC012866, 2017. a
Petrenko, A. A.: Variability of circulation features in the Gulf of Lion NW Mediterranean Sea. Importance of inertial currents, Oceanol. Acta, 26, 323–338, 2003. a, b, c
Piterbarg, L., Taillandier, V., and Griffa, A.: Investigating frontal variability from repeated glider transects in the Ligurian Current (North West Mediterranean Sea), J. Marine Syst., 129, 381–395, 2014. a, b, c, d
Pollard, R. and Millard, R.: Comparison between observed and simulated wind-generated inertial oscillations, Deep Sea Research and Oceanographic Abstracts, 17, 813–821, https://doi.org/10.1016/0011-7471(70)90043-4, 1970. a
Poulain, P.-M., Gerin, R., Mauri, E., and Pennel, R.: Wind Effects on Drogued and Undrogued Drifters in the Eastern Mediterranean, J. Atmos. Ocean. Tech., 26, 1144–1156, https://doi.org/10.1175/2008JTECHO618.1, 2009. a, b
Ralph, E. A. and Niiler, P. P.: Wind-Driven Currents in the Tropical Pacific, J. Phys. Oceanogr., 29, 2121–2129, https://doi.org/10.1175/1520-0485(1999)029<2121:WDCITT>2.0.CO;2, 1999. a
Rio, M.-H. and Hernandez, F.: High-frequency response of wind-driven currents measured by drifting buoys and altimetry over the world ocean, J. Geophys. Res.-Oceans, 108, 3283, https://doi.org/10.1029/2002JC001655, 2003. a, b, c, d, e
Röhrs, J., Sperrevik, A. K., Christensen, K. H., Broström, G., and Breivik, Ø.: Comparison of HF radar measurements with Eulerian and Lagrangian surface currents, Ocean Dynam., 65, 679–690, 2015. a
Rubio, A., Taillandier, V., and Garreau, P.: Reconstruction of the Mediterranean Northern Current variability and associated cross-shelf transport in the Gulf of Lions from satellite-tracked drifters and model outputs, J. Marine Syst., 78, S63–S78, 2009. a
Sammari, C., Millot, C., and Prieur, L.: Aspects of the seasonal and mesoscale variabilities of the Northern Current in the western Mediterranean Sea inferred from the PROLIG-2 and PROS-6 experiments, Deep-Sea Res., 42, 893–917, 1995. a, b, c, d
Schaeffer, A. and Roughan, M.: Influence of a western boundary current on shelf dynamics and upwelling from repeat glider deployments, Geophys. Res. Lett., 42, 121–128, https://doi.org/10.1002/2014GL062260, 2015. a
Schaeffer, A., Molcard, A., Forget, P., Fraunié, P., and Garreau, P.: Generation mechanisms for mesoscale eddies in the Gulf of Lions: radar observation and modeling, Ocean Dynam., 61, 1587–1609, 2011. a
Schroeder, K., Josey, S. A., Herrmann, M., Grignon, L., Gasparini, G. P., and Bryden, H. L.: Abrupt warming and salting of the Western Mediterranean Deep Water after 2005: Atmospheric forcings and lateral advection, J. Geophys. Res., 115, C08029, https://doi.org/10.1029/2009JC005749, 2010. a
Sentchev, A., Forget, P., Barbin, Y., and Yaremchuk, M.: Surface circulation in the Iroise Sea (W. Brittany) from high resolution HF radar mapping, J. Marine Syst., 109–110, S153–S168, 2013. a
Sentchev, A., Forget, P., and Fraunié, P.: Surface current dynamics under sea breeze conditions observed by simultaneous HF radar, ADCP and drifter measurements, Ocean Dynam., 67, 499–512, https://doi.org/10.1007/s10236-017-1035-6, 2017. a, b
Stanichny, S. V., Kubryakov, A. A., and Soloviev, D. M.: Parameterization of surface wind-driven currents in the Black Sea using drifters, wind, and altimetry data, Ocean Dynam., 66, 1–10, https://doi.org/10.1007/s10236-015-0901-3, 2016. a, b
Stewart, R. H. and Joy, J. W.: HF radio measurements of surface currents, Deep Sea Research and Oceanographic Abstracts, 21, 1039–1049, https://doi.org/10.1016/0011-7471(74)90066-7, 1974. a
Taupier-Letage, I. and Millot, C.: General hydrodynamical features in the Ligurian Sea inferred from the DYOME experiment, Oceanol. Acta, 9, 119–131, 1986. a, b
Tokeshi, R., Ichikawa, K., Fujii, S., Sato, K., and Kojima, S.: Estimating the geostrophic velocity obtained by HF radar observations in the upstream area of the Kuroshio, J. Oceanogr., 63, 711–720, https://doi.org/10.1007/s10872-007-0062-1, 2007. a, b, c
Vignudelli, S., Cipollini, P., Astraldi, M., Gasparini, G. P., and Manzella, G.: Integrated use of altimeter and in situ data for understanding the water exchanges between the Tyrrhenian and Ligurian Seas, J. Geophys. Res.-Oceans, 105, 19649–19663, https://doi.org/10.1029/2000JC900083, 2000. a
Weber, B. L. and Barrick, D. E.: On the Nonlinear Theory for Gravity Waves on the Ocean's Surface. Part I: Derivations, J. Phys. Oceanogr., 7, 3–10, https://doi.org/10.1175/1520-0485(1977)007<0003:OTNTFG>2.0.CO;2, 1977. a
Weller, R. A., Rudnick, D. L., Eriksen, C. C., Polzin, K. L., Oakey, N. S., Toole, J. W., Schmitt, R. W., and Pollard, R. T.: Forced ocean response during the Frontal Air-Sea Interaction Experiment, J. Geophys. Res.-Oceans, 96, 8611–8638, https://doi.org/10.1029/90JC02646, 1991. a
Whitney, M. M. and Garvine, R. W.: Wind influence on a coastal buoyant outflow, J. Geophys. Res.-Oceans, 110, C03014, https://doi.org/10.1029/2003JC002261, 2005. a, b
Wijffels, S., Firing, E., and Bryden, H.: Direct Observations of the Ekman Balance at 10∘ N in the Pacific, J. Phys. Oceanogr., 24, 1666–1679, https://doi.org/10.1175/1520-0485(1994)024<1666:DOOTEB>2.0.CO;2, 1994. a
Yuan, Y., Castelao, R. M., and He, R.: Variability in along-shelf and cross-shelf circulation in the South Atlantic Bight, Cont. Shelf Res., 134, 52–62, https://doi.org/10.1016/j.csr.2017.01.006, 2017. a, b
- Abstract
- Introduction
- Background, statement of the problem, and definitions
- Data and methods
- Water column stratification and geostrophic variability, and effects of wind forcing
- Direct surface response to the wind
- Summary and conclusions
- Data availability
- Competing interests
- Special issue statement
- Acknowledgements
- References
- Abstract
- Introduction
- Background, statement of the problem, and definitions
- Data and methods
- Water column stratification and geostrophic variability, and effects of wind forcing
- Direct surface response to the wind
- Summary and conclusions
- Data availability
- Competing interests
- Special issue statement
- Acknowledgements
- References