the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Turbulent length scales in a fast-flowing, weakly stratified, strait: Cook Strait, New Zealand
Craig L. Stevens
There remains much to be learned about the full range of turbulent motions in the ocean. Here we consider turbulence and overturn scales in the relatively shallow, weakly stratified, fast-flowing tidal flows of Cook Strait, New Zealand. With flow speeds reaching 3 m s−1 in a water column of ∼300 m depth the location is heuristically known to be highly turbulent. Dissipation rates of turbulent kinetic energy ε, along with the Thorpe scale, LT, are described. Thorpe scales, often as much as one-quarter of the water depth, are compared with dissipation rates and background flow speed. Turbulent energy dissipation rates ε are modest but high for oceans, around W kg−1. Comparison of the buoyancy-limit Ozmidov scale LOz suggest the Cook Strait data lie for the majority of the time in the LOz > LT regime, but not universally. Also, comparison of direct and LT-based estimates of ε exhibit reasonable similarity.
It is well-established that turbulent mixing in the ocean is intermittent and patchy (see Waterhouse et al., 2014 for a synthesis). Thus, there is substantial benefit in seeking out extreme conditions to fully capture the global energy budget. Tidal motion, through one pathway or another, drives significant mixing in the ocean. While is it understood that this mixing can influence ecological functioning (e.g. Scott et al., 2010; Koch-Larrouy et al., 2015), knowledge gained in shallow coastal situations is also applicable in deeper ocean conditions (e.g. Dale and Inall, 2015). Here we consider these issues in the fast flows of a large tidally driven passage, Cook Strait, a situation that couples a relatively large vertical extent with substantial inertial forcing.
Table 1Comparison of approximate representative strait scales (extended from Helfrich, 1995; Hogg et al., 2001).
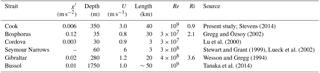
In a 1999 paper reviewing the first shear probe measurements of oceanic turbulence, Stewart and Grant (1999) described the flows in Seymour Narrows (Discovery Passage, Canada) as sustaining Reynolds numbers (Re) amongst the “largest in the universe”. True or not, it is a useful benchmark and discussion point. There is a tendency to ignore the Reynolds number in geophysical flows as they are typically so very large, primarily because of the length scales involved. Cook Strait has comparable flow speeds to Discovery Passage but is around 4 times the depth, and so suggests a larger bulk Re. From the diapycnal diffusion perspective, despite this highly turbulent large-scale flow, stratification clearly persists through the strait (Stevens, 2014).
Of practical concern here is the amount of kinetic energy lost from the system via dissipation (i.e. the rate of dissipation of turbulent kinetic energy, ε) as this plays an important role in adequately simulating ocean systems where there is a high dynamic range of variability. This then informs quantification of turbulent diapycnal diffusion, which is a balance of turbulent overturning against a stably stratified background as characterized by the buoyancy frequency squared: N2 = . Wesson and Gregg (1994) set the scene for the research theme surveying turbulence quantities in the exchange-dominated Straits of Gibraltar, where they were able to quantify key turbulence parameters as driven both by internal shear and boundary mixing.
Mater and Venayagamoorthy (2014) lay out a pictorial representation of length scales in stratified turbulence. The observed Thorpe overturning scale, LT, is a relatively measurable quantity associated with ocean structure and can be considered the energy-baring scale. This is constrained by the Ozmidov scale () that identifies the limits to growth of eddies and also the Kolmogorov length scale (, ν is kinematic molecular viscosity) where turbulent fluctuations are absorbed by viscous damping forces. It is common to seek to relate the observable LT to mechanistically relevant quantities like turbulent kinetic energy, and its dissipation rate ε (e.g. Dillon, 1982; Mater et al., 2013). This enables ε to be estimated from a combination of relatively achievable measurements. Mater et al. (2015) and Scotti (2015) explore the veracity of this long-used approach in a variety of conditions. Typically, this has been examined in the deep ocean and so biased away from the more energetic conditions.
The present paper uses microstructure and overturn data to report on the stratified boundary layer response and mixing in the unique situation of Cook Strait as an aid extending our knowledge around oceanic turbulence. It is instructive to compare Cook Strait with other straits of note (Table 1) as it is essentially oceanic, and so relatively weakly stratified, with the g′ (the modified gravity , Δρ being the bulk vertical density difference relative to a representative reference density ρ and g is gravitational acceleration) in Table 1 being a maximum as observed through an annual cycle. The table includes representative estimates of the Reynolds number and a bulk Richardson number (Ri = ) where Δu is the top-bottom velocity difference (Ri ≲1 implies weak stratification). The remarkable aspect for Cook Strait is its tidally induced currents and so it constitutes a useful location (Fig. 1) because of the very fast tidal flows in reasonably deep water. A number of questions arise: (i) Do we actually observe high dissipation rates? (ii) How does the Thorpe scale compare with the Ozmidov scale? (iii) Following from this, can a fixed ratio be assumed and so allow estimation of ε? (iv) How does the turbulence compare with other straits?
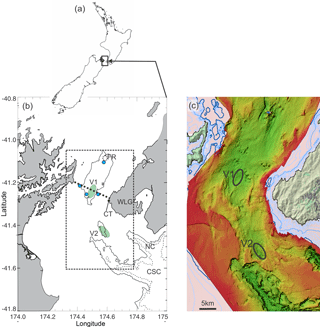
Figure 1Location showing (a) New Zealand and, within this, (b) Cook Strait Narrows is bounded by Cape Terawhiti (CT) to the east and the headlands of the (shaded) Marlborough Sounds to the west and with the Cook Strait and Nicholson Canyon to the south (CSC and NC). The 200 (solid) and 400 m (dashed) depth contours are marked, as well as the shoal at Fishermans Rock (FR). ADCP moorings are marked with blue circles. The microstructure data come from profile regions V1 and V2.
Cook Strait, the channel separating New Zealand's North and South islands, connects the eastern Tasman Sea to the western Pacific at 42∘ S (Fig. 1). At its narrowest point it is 22 km across, with 210 and 350 m average and maximum depths, respectively. Its fast-flowing tidal currents have been the focus of a number of studies, including the notable observation that the semi-diurnal tide is around 140∘ out of phase when considering the opposite ends of the Strait (Heath, 1978). This phase difference drives substantial flows, reaching as high as 3.4 m s−1 during spring tides (Stevens et al., 2012).
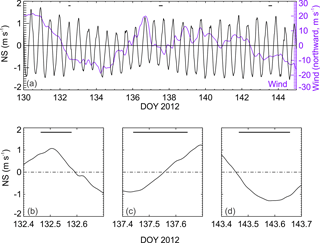
Figure 2Sampling conditions showing average N–S (north-south aligned flow with northward being positive) water column velocity between 60 and 100 m depth and wind speed – both filtered with an hourly low-pass filter. The bars show microstructure sample periods. These bars are expanded in the daily sampling relative to tidal conditions is shown in (b), (c) and (d).
Background velocity data come from two instrumented moorings deployed at the “third points” across the narrows (Fig. 1) for a period spanning 2 years, in two deployments, starting in August 2010 and continuing through until September 2012. Each mooring contained an upwards-looking Teledyne-RDI 75 kHz ADCP (acoustic Doppler current profiler) mounted in a Flotation Technologies syntactic foam float and moored with 600 kg of iron and 10 m of chain. The ADCPs logged at 10 min intervals, sampling into 8 m depth bins. Each float contained a Seabird microcat (SBE 39) conductivity–temperature–depth (CTD) sensor placed beneath the ADCPs, which sampled at 5 min intervals. This enabled comparison with satellite-derived sea surface temperature for the centre of the strait. With such high tidal flow rates it is not possible to adequately moor instrumentation near the surface as the mooring is “knocked down”, meaning that near-surface data are not observed during high flows.
Microstructure profiles were recorded with a VMP500 (Vertical Microstructure Profiler – Rockland Oceanographic, Victoria Canada) instrument. This free-fall, loose-tether package supported two shear probes, two fast thermistors, accelerometers and a Seabird Electronics (SBE) conductivity and temperature sensor pair. A total of 34 profiles were collected using the 14 m twin-hulled jet-boat Ikatere during a number of expeditions from 2010 to 2012 but the bulk come from a 12-day period in 2012. The timing of the profiles during the 2012 sampling is shown in Fig. 2. It is difficult to capture extended periods of contiguous sampling because a vessel suitably manoeuvrable to conduct the experiments is prone to weather limitations. Sampling over 3 days in 2012 centred on periods spanning northward, turning and southward tidal flows (Fig. 2).
The profiler captures temperature and conductivity data; however, this sensor pair is un-pumped (to reduce vibration contamination of the shear probe) and so has a slow actual conductivity response and is relatively sensitive to spiking induced by response-time mismatch. A fast-response conductivity sensor was included in the measurements, which gets around the response issue but had its own idiosyncrasies due to fouling and will not be examined here. Correcting un-pumped salinity estimates is becoming more common with ocean glider applications (Timmermans and Winsor, 2013); however, the present profiling application is a more rigorous challenge. Being a derivative quantity, N2 emphasizes any spikes or noise. The bulk temperate–salinity relationship for the region is relatively well-ordered and so this enables density for each profile to be calculated using the high-quality temperature and the bulk T–S relationship (for that profile). While this would not be particularly reliable for absolute density estimation, it is sufficient to generate an estimate of the buoyancy frequency squared, N2. The density profile contains fine-scale overturns and this also results in a challenge for N2 estimation. Mater et al. (2015) review methods for calculating N2, and here the patch-average N2 is used based on a density-sorted profile. The removal of salinity spikes from the original profile data was found to have the greatest impact on the N2 estimation.
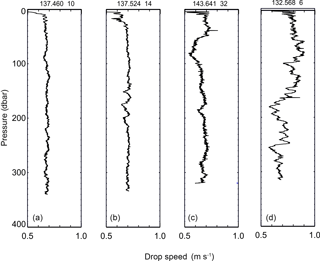
The microstructure data were recorded using a pair of orthogonally mounted shear sensors. The shear data were recorded at 512 Hz and processed to resolve the dissipation rate ε (Wolk et al., 2002; Macoun and Lueck, 2004). This involved first de-spiking to remove spurious transient records, most likely due to encountering biological organisms. The dissipation can then be determined from the integration of shear. However, before this is calculated the useful limit of the data needs to be determined. Unlike many microstructure applications, there is a high signal-to-noise ratio. What challenges these data is profiler vibration (Wolk et al., 2002). The profiler also samples package motion using a triaxial accelerometer and this provides a cut-off point in the useful shear data, beyond which the spectrum is padded with the Nasmyth spectrum (Macoun and Lueck, 2004). The data were separated into dissipation rate estimates from each sensor using 5 m depth bins. The requirement is that the profiler be passing through the water steadily over the period of any given bin. Vertical speed is resolved from the pressure sensor so that conversion to wavenumber requires reliable velocity estimation (Wolk et al., 2002). Figure 3 shows the profiler drop speed, and its variability reflects the degree of vertical turbulent motion, which reached as much as 0.1 m s−1. The upper portion of the water column includes an acceleration period, and sometimes wave effects are apparent. Deeper down it is clear that there is variability in the character of the drop speed variations, although over periods longer than that required for the 5 m vertical bins. The shear spectrum was generated for each depth bin and then compared with a pseudo shear spectrum generated from the accelerometer data. The crossover point allowed identification of the noise limit in the shear spectrum, above which the signal was replaced this with the Nasmyth model spectrum. With the generally high dissipation rates this was not a particularly significant correction.
Having resolved ε and N2, a number of derived quantities could then be calculated. The Ozmidov scale identifies the upper bound at which eddies should “feel” the stratification. One might expect overturns, as identified using the LT, to be equal to or smaller than LOz. Dillon (1982) observed the ratio to be . This calculation struggles in regions of weak stratification where locally small N2 results in a very large scale. This makes sense as weak stratification fails to retard turbulence. However, it can also lead to non-physical outcomes, as the scale will eventually exceed water depth. The vertical (∼ diapycnal) diffusivity Kz is commonly calculated as , with Γ=0.2 an assumed constant. While convenient, there is a good deal of evidence to suggest that Γ is not constant – for example Bluteau et al. (2013) suggested that it resulted in an order of magnitude overestimation of mixing rate. This will be returned to in the Discussion.
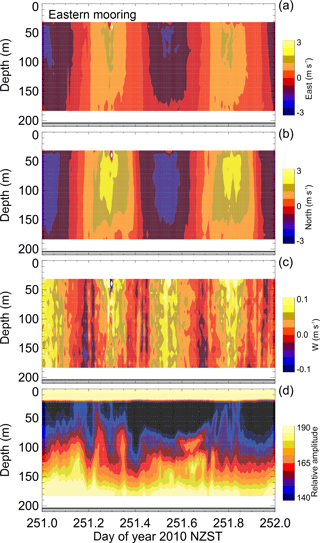
Figure 4Velocity data from eastern side of strait showing (a) east–west (eastward is positive), (b) north–south (northward is positive), (c) vertical velocities and (d) backscatter amplitude.
Given the nature of the salinity structure, as with Wesson and Gregg (1994) and others, we use the more precisely known temperature to define overturns. The Thorpe scale LT is often taken to be some average of displacement scales over a given depth bin. However, this fails to recognize that the enclosed nature of an overturn can set a natural envelope to the estimation (Mater et al., 2015), so that moving through the profile and summing displacements, one can see the start of an overturn and then maintain the sum of displacements until the net displacement is brought back to zero (within some error). This has the same effect as the centred length scale proposed by Imberger and Boahash (1986) whereby displacements were aggregated at the centre of the overturn. By using the microstructure temperature sensor record, the lower limit to this scale has a smaller spatial resolution than a traditional CTD thermistor sensor.
The nature of the high flow rates in the strait is illustrated with a day-long sub-section of the 2 years of velocity data from the eastern side of the Strait (Fig. 4). The relatively poor data depth coverage is due to instrument tilt, which while remaining within usable tolerances, does exacerbate side-lobe interference from the surface. While predominantly north–south, the vector sum indicates local speeds reaching 3 m s−1 at a water depth of around 30 m (speeds above are not recorded). The flow at this location is not symmetric, with southward flows being 20 %–50 % smaller. Vertical velocities reach 0.1 m s−1 with greater high frequency variability when compared to the horizontal flow signal – this compares with variation observed in profiler drop speed (Fig. 3). Backscatter structure has some correlation to the flow speed, with the fast flow periods heralding increased backscatter through most of the measured water column. The bulk velocity shear is described in Stevens (2014) and the asymmetry is particularly clear, with levels reaching maximum values of ±0.01 s−1.
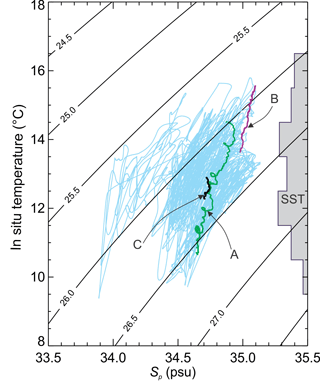
Figure 6Temperature and salinity (Sp) from the seabed sensors on the moorings with profile data overlain (see text for details) and σT contours. The arbitrarily scaled histogram on the right-hand margin shows the distribution of satellite-derived sea surface temperature (SST).
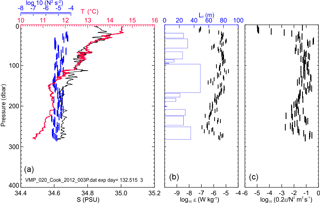
Figure 7Profile A from day 132, 2012, showing (a) temperature, salinity and buoyancy frequency squared (N2); (b) LT and ε; and (c) proxy for vertical diffusivity 0.2ε∕N2. Note the profile extends over the full depth of the water column.
The comparison of moored and remotely sensed data (Fig. 5) suggests that, despite the energetic nature of the strait, it is not fully mixed during the austral summer (Stevens, 2014). The data are insufficient to indicate if the strait is often stratified in density but it is clearly not homogeneous in temperature for a significant portion of the year. Temperature differences between bed and surface are as large as 3 ∘C (primarily in the November–April period). Considering the same data in T–S space (Fig. 6) shows the seabed and surface temperatures spanning the same range essentially. Three selected microstructure profiles (A, B and C) demonstrate the vertical structure with vertical density differences reaching as high as 0.5 kg m−3 over the full depth of the water column. The low salinity data (S < 34.4) are seen in Stevens (2014) and result in a 5-month-long period at the start of 2012 where the eastern mooring sustained lower S, but kept a similar T to other moorings at the time. The profiles come from right at the end of this period and so do not exhibit anomalous salinities.
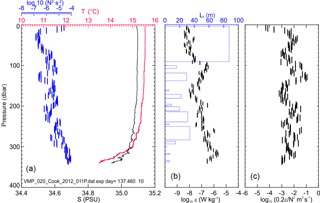
Figure 8Profile B from day 137, 2012, showing (a) temperature, salinity and buoyancy frequency squared (N2); (b) LT and ε; and (c) proxy for vertical diffusivity 0.2ε∕N2. Note the profile extends over the full depth of the water column.
Before considering the turbulence data en masse, it is useful to look at some details of selected profiles. The example profile A (Fig. 6) is one of the more strongly stratified observed in the strait. The details of this profile (Fig. 7) illustrate the effect of the conductivity sensor being un-pumped. However, the profile structure at the macroscale is monotonic in temperature and so temperature displacements are dynamically meaningful. Stratification persisted throughout the water column, with N2 being around 10−5 s−2. Neither the N2 nor the dissipation rate structure varied greatly through the water column. Near-surface values of ε were low, but increased to hold a near-constant level through most of the water column, then rising near the bed. The large central overturn, as identified with the Thorpe analysis, contained the majority of the vertical variability in ε in the profile, supporting the decision to keep LT and ε calculations separate. The diffusivity proxy (Fig. 6c) is notable that in this one instance, the combined ε and N2 imply Kz exceeds 0.1 m2 s−1, i.e. it is very large. As will be returned to in the Discussion, Bluteau et al. (2017) find that these large mixing events might themselves be underestimated.
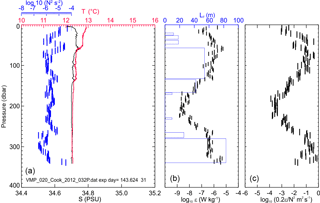
Figure 9Profile C from day 143, 2012, showing (a) temperature, salinity and buoyancy frequency squared (N2); (b) LT and ε; and (c) proxy for vertical diffusivity 0.2ε∕N2. Note the profile extends over the full depth of the water column.
The profile B (Fig. 8) differs from profile A in that it has a large quasi-homogeneous upper portion of the water column. Stratification results in a reduced N2 are as low as 10−7 s−2 but increase with depth. The dissipation rate structure increased with depth through the water column (i.e. in tandem with the stratification). The weak stratification was still sufficient that overturn scales were small throughout the water column, except for the large upper overturn that exceeds 80 m in scale. Interestingly this coincided with an upper layer of low dissipation rate. However, this may be due to a thin low salinity surface layer (see Bowman et al., 1983) with a compensating low temperature, and this is a case where density rather than temperature should be used to gauge overturns. In this example, the combined ε and N2 imply a Kz proxy peaking at around 0.1 m2 s−1 but being mostly an order of magnitude smaller.
The final profile example described here, profile C (Fig. 9), sustains a lower quasi-homogeneous region of the water column. Stratification results in N2 having a baseline around 10−6 s−2 but significantly increasing at the interface zones. The dissipation rate structure here is bi-modal with a mid-depth minimum. Overturn scales followed the dissipation rate trend with an especially large structure near the bed. Dissipation rates at the bed exceeded W kg−1. The variability in ε dominates that of the N2, so that the Kz proxy structure mirrors ε closely, peaking just under 1 m2 s−1 near the bed. This extremely high value is to be expected in a flow known to move large boulders.
4.1 Are the dissipation rates actually large?
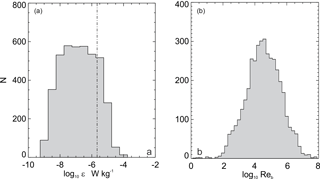
The distribution of dissipation rate (Fig. 10a) shows that the level of turbulent kinetic energy (as inferred by ε) extends over 5 orders of magnitude. While the linear average is around W kg−1, extrema can exceed 10−4 W kg−1. In addition, most unusually, there were almost no estimates down at the instrument noise floor around 10−10 W kg−1. Scaling these estimates over depth, taking the perspective of a numerical modeller looking to resolve friction losses through a Strait, suggests between 0.6 and 30 W m−2 are lost through turbulent dissipation (cf. Bāb al Mandab with a maximum around 0.2 W m−2, Jarosz et al., 2011).
It is easy to ignore bulk Re in ocean physics, assuming correctly that any Re calculation will be “large”. However, at the turbulence scales buoyancy can potentially affect overturns and re-stratification. The turbulent buoyancy Reynolds number Reb () identifies how velocity fluctuations, and any associated buoyancy flux, evolve and decay. In the present Cook Strait data, the majority of Reb estimates exceed 100, with the peak of the distribution being around 5×104 (Fig. 10), confirming that the turbulence is “energetic” (Mater et al., 2013). The larger Reb values exceed 107, which is primarily due to the small N that approaches the levels of detection. This is larger than the range observed by Wesson and Gregg (1994) who, in the much stronger stratification of Gibraltar, saw Reb values more commonly around 102–103, but still with some Reb reaching 105 or more.
It is a particularly challenging environment to profile in, due to the fast flows and strong winds, combined with the relatively long profile durations. A profile and retrieval pair would take around 30 min to complete, in which time the vessel would have shifted as much as several kilometres. Keeping the vessel on station was not possible as the instrument line would pay out so great a distance that line drag would mean that free fall would cease. Moving the vessel with the line proved too risky in terms of entanglement. Consequently, sequences of two to three profiles were recorded before repositioning the vessel.
Other sampling strategies have been considered, both as a comparison and as a way to extend the dataset. Ocean glider-mounted microstructures would be affected by the substantial vertical flows. Bed-mounted turbulence sampling will be subject to mooring blow-down so that the sampling package will be constantly moving through the vertical. Surface-floating gear is affected by the very substantial surface wave field. In the instance of Cook Strait, free-drifting mooring-based sampling is unlikely to get regulatory approval due to the potential for fouling on submarine high-voltage DC cables that cross the strait.
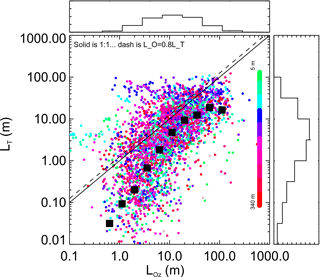
Figure 11Scatter plot of LT vs. LOz colour-coded by depth. Lines for unity and for LOz=0.8LT are shown and associated histograms of length scales are shown also. Averages were calculated in log10 space and 0.5 m was considered a lower bound for LOz.
Traditional microstructure profiling thus appears to be the most suitable option for now as we seek to capture a greater variety of conditions, especially during the spring tides. The fast flows mean that an ability to rapidly reposition is thus an advantage, meaning a smaller vessel in good weather was a better option than a larger vessel able to handle rougher conditions. The end result of all the trade-offs was that we have yet to work out a way to capture a regular sequence of profiles through a tidal cycle in effectively the same location. However, we have built up a dataset through all phases of the tide, though only from a limited set of seasonal conditions and not in the very fastest flows.
4.2 Does the Thorpe scale vary systematically with the Ozmidov scale?
A cross-comparison of LT with LOz (Fig. 11) shows a systematic co-variation but one that is far from 1:1. In addition, no LT greater than 100 m was observed despite the water column exceeding 3 times this and weak stratification. However, the calculated LOz is not actually physically constrained and in several instances, it exceeds the water depth. Considering log10 distributions of LT with LOz, the observed Thorpe displacement scale LT is substantially smaller than the buoyancy-controlled limit LOz, by an order of magnitude at smaller length scales. The two estimates come closest at around LT∼10 m (being around 50 % of LOz). Wesson and Gregg's (1994) observations of turbulence quantities in the Strait of Gibraltar found that the LOz (LB in their notation) compared essentially 1:1 with LT, with most estimates falling within a factor of 4 either side. They also found this degree of scatter held throughout the water column. This differs from that seen here (Fig. 12), where the LT is substantially smaller than the LOz by as much as a decade at smaller scales. The scatter is also larger in the present data as this also is around a decade either side of the mean value. This latter point may be driven by the present noise-rejection conditions resulting in fewer very small LOz (say < 0.5 m), whereas the Gibraltar data drop to as low as 10−2 m. In addition, the present use of the microstructure sensors to estimate LT allows this to extend to smaller values. Furthermore, the Cook data exhibit a possible split in behaviour around LOz=10 m, whereas the Gibraltar data only hints at this. Making the same comparison with the Dunkley et al. (2015) Gulf of Aqaba observations ranging over LT=0.1–10 m, the distribution is almost a mirror reflection around the 1:1 line from that observed in Cook Strait. In the Gulf of Aqaba results, the LT exceeds the LOz by as much as an order of magnitude on average – a trend also seen in the Bluteau et al. (2013) data. Finnigan et al. (2002) used the LT approach to estimate turbulence in the vicinity of a submarine ridge, and cross-comparison with strain-derived estimates of e.g. Frants et al. (2013) suggested it was applicable at least where there was detectable stratification. However, the dissipation rate levels were around 10−9 W kg−1, 3 orders of magnitude less than in the present situation. While field studies are typically compromised in some way, complementary analyses through direct numerical simulation (e.g. Smyth et al., 2001) provides supporting evidence that there should be a systematic variation in the empirical overturn scale (LT) and the buoyancy-induced limit to overturns (LOz). This approach suggests that the variation in the ratio of the two scales is an indication of the age of the mixing event, with LOz increasing relative to LT, and so that scatter in real observations reflects the random age captured by sporadic profiling.
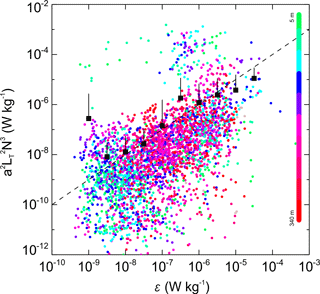
Figure 13Comparison of dissipation resolved from the LOz with the direct measure of ε. Averages were calculated in log10 space for ε and all length-scale-based estimates in that bin were collated. Here the average and average +1 standard deviation are shown with a circle–line pair and the average in log10 space is shown as a square. The averages excluded outliers in the surface water as described in the text.
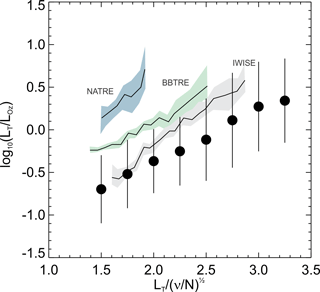
One of the challenges in ocean turbulence is that studies are so intense, focused and idiosyncratic that they tend to be analysed in isolation and rarely synthesized. As a counter-example to this, Mater et al. (2015) collated three open-ocean turbulence experiments from (i) the North Atlantic at around 3000 m (NATRE, Toole et al., 1994), (ii) the Brazil Basin mid-Atlantic at around 3000 m (BBTRE, St. Laurent et al., 2001) and (iii) Luzon Straits at around 2500–3000 m, (IWISE, Alford et al., 2011). Here we consider the present data in this context (Fig. 12). The ratio of LT to LOz in these deep-water experiments was considered against a LT non-dimensionalized by the length scale extracted from viscosity and buoyancy (, representing the distance momentum can diffuse in a time N−1. All follow the same trend of the ratio LT∕LOz growing with increasing eddy size. All but the NATRE data have significant proportion of data showing LT < LOz. The present Cook Strait data illustrate this aspect most strongly nearing an order of magnitude smaller at low LT. Furthermore, the present data extend into the largest non-dimensional LT space. Mater et al. (2015) suggest that while the experiments are in deep water they are still constrained vertically by convective scales.
A comparison of direct shear probe dissipation rate estimates of LOz and the Thorpe scale LT indicates a broadly comparable trend but that the comparison is not 1:1 (Fig. 11), with the departure growing for larger scales. There looks to be a bias towards high LT values for low LOz value at shallow depths. Using the Dillon (1982) approach of considering the and assuming LOz∕LT is fixed such that LOz=aLT, we then arrive at a simple expression for ε (Fig. 13). This compares the dissipation rates from each LT overturn with both the direct and log10-based average ε within that overturn. The direct average (squares) provides a close comparison between observed and estimated ε. This agreement holds from W kg−1 through to W kg−1, with only one or two departures, the most notable being at 10−9 W kg−1 where it is biased high by a very larger outlier that is so anomalous that it should possibly be discounted. There is an obvious family of outliers in the upper 30 m of water that are anomalously high in terms of the parametrized estimate of dissipation rate. Most likely this is a result of some surface-driven stratification effect that either (i) affects turbulence in some systematic way or (ii) confounds the temperature-based density correction. The log-based comparison is around an order of magnitude smaller. This is included in order to compare this representation with Fig. 11.
While the LT never approaches the full water depth, they are large given the flow speeds. Stevens (2014) measured velocity shear at bulk scales (i.e. resolved from 8 m ADCP bins) reaching as high as 0.01 s−1. The velocity variation over an eddy of LT=100 m in a flow with a velocity shear of 0.01 s−1 is 1 m s−1. This is comparable, but not greater than, background speeds suggesting that it might influence the degree of isotropy by straining eddy structure in the horizontal direction. A similar effect should be expected in slower but much deeper systems such as the Bussol Strait (Tanaka et al., 2014; Bryden and Nurser, 2003).
4.3 Implications for, and of, mixing rate estimates
The Γ=0.2 “constant” is a clear point of contention in the literature (e.g. Dunkley et al., 2012; Bluteau et al., 2013; Mashayek et al., 2013). Bluteau et al. (2017) develops an approach that takes microstructure profiles and resolves the diffusivity “directly”, fitting a model for dissipation of thermal variance to the convective-inertial subrange (i.e. lower wavenumbers than the dissipation scale). The Bluteau et al. (2017) analysis suggests that improved estimation of the thermal diffusivity indicates that the fixed mixing coefficient might underestimate mixing by a factor of 5 in the mean, especially for the more turbulent events. Extending this by applying the Osborne diffusivity method sees an average diffusivity of around 0.04 m2 s−1 and exceeding 1 m2 s−1 (Fig. 10b). One might expect a 300 m water column to then be homogenized in a time ( h, but this might be as little as 5 h if the Bluteau et al. (2017) increased estimate of Kz were to hold. Tidal excursions due to the semi-diurnal tide are insufficient to flush the strait in a single cycle. Indeed, with a net drift of around 0.02–0.1 m s−1 (Stevens, 2014) it takes many tidal cycles. This suggests that, at these most energetic of mixing conditions, we should not expect to see a stratified water column as it should get mixed over the multiple tidal cycles it takes for water to clear the strait. The bulk top-bottom observations (Fig. 5) counter this as, for some of the year at least, there is clearly a scalar gradient. Possibly, the observations need to be restructured and collected by drifting with the flow to better follow the evolution of mixing.
Lafuente et al. (2013), in their exploration of the impact of vertical diffusion of biologically relevant scalars in the Straits of Gibraltar, found a highly two-dimensional situation in which the mixing is highly spatially variable, with the presence and location of an internal hydraulic jump being very important. In a similar way to Cook Strait, their simulations show, despite the reasonable tides and strong estuarine circulation, it takes some time for well-mixed water to exit the system. Lafuente et al. (2013) set their background vertical diffusivity to 10−7 m2 s−1 and also prescribed a maximum of 10−2 m2 s−1 in order to “avoid unrealistically high values”. While having the potentially very small N2 in the denominator for Kz is problematic, the very large ε and LT make it reasonable to assume, with finite N, that the larger Kz estimates are useful in a bulk sense. This suggests future work could apply the approach of Bluteau et al. (2017) to profile data to capture the large Kz events.
While the focus here is on vertical structure and mixing, the horizontal perspective is also of value. The Strait has been identified as a dividing line in terms of ecological structure (e.g. Forrest et al., 2009). The implication is that there is not a great deal of transverse (across-strait) transport. This supports the focus of the present work on the vertical structure. Furthermore, over the time it takes to drift through the strait, all vessel tracks tended to be on an axis aligned with the strait. Over these scales of time and space the strait itself is bathymetrically reasonably consistent. Future studies should focus on adequately quantifying across-strait mixing, the associated drivers and the moderating influence of vertical mixing.
4.4 How does the turbulence compare with other straits?
While the present focus is on turbulent length scales rather than their oceanographic context, studies examining flows through stratified straits, both in a net sense and in exchange conditions, classically view the mechanics in terms of non-mixing internal hydraulics (Helfrich, 1995; Hogg et al., 2001). This enables identification of phenomena such as control points and the presence of hydraulic jumps. The extension to consider the role of turbulence and mixing in influencing the system uses bulk estimates of Kz (Hogg et al., 2001). They were able to demonstrate that by varying the mixing coefficient, a strait system could vary between inviscid hydraulic conditions and a mixing layer. This highlights the need for more direct observations of mixing in such situations.
While Stewart and Grant (1999) identify the high Reynolds number in Seymour Narrows (Discovery Passage, British Columbia), it is clear that deeper coastal systems like Cook Strait and much deeper oceanic constrictions (e.g. Tanaka et al., 2014) create even higher Re conditions. It is difficult to draw general conclusions describing strait behaviour from any one situation, as Gregg and Özsoy (2002) noted when quoting Tolstoy to highlight field idiosyncrasies. While the quote was in the context of the Bosphorus Strait, the canonical strait at this scale is probably Gibraltar, the scene of some of the first systematic turbulence quantification (Wesson and Gregg, 1994). These authors state that “rather than being definitive, these results are only the beginning of turbulence measurements in the Strait of Gibraltar”. While this has not really turned out to be the case for Gibraltar, the approach and results spawned a range of studies in comparable systems (Table 1), with the ensemble providing a natural laboratory for exploring a range of ocean mixing phenomena.
The data are available by contacting the author.
The author declares that there is no conflict of interest.
The author would like to acknowledge colleagues who have aided in the work,
in particular Brett Grant, Mark Hadfield, Fiona Elliott, Craig Stewart, Ross Vennell, Murray Smith, Steve Chiswell, Graham Rickard, Rebecca McPherson and
Joe O'Callaghan. Two anonymous reviewers are thanked for providing
constructive comments on an earlier version of this paper. The support of NIWA Core Funding, the New Zealand Sustainable Seas
National Science Challenge and the Royal Society Te Apārangi Marsden
Fund is acknowledged.
Edited by: Eric J. M. Delhez
Reviewed by: two anonymous referees
Alford, M. H., MacKinnon, J. A., Nash, J. D., Simmons, H., Pickering, A., Klymak, J. M., Pinkel, R., Sun, O., Rainville, L., Musgrave, R., and Beitzel, T.: Energy flux and dissipation in Luzon Strait: Two tales of two ridges, J. Phys. Oceanogr., 41, 2211–2222, 2011.
Bluteau, C. E., Jones, N. L., and Ivey, G. N.: Turbulent mixing efficiency at an energetic ocean site, J. Geophys. Res.-Ocean., 118, 4662–4672, https://doi.org/10.1002/jgrc.20292, 2013.
Bluteau, C. E., Lueck, R. G., Ivey, G. N., Jones, N. L., Book, J. W., and Rice, A. E.: Determining mixing rates from concurrent temperature and velocity measurements, J. Atmos. Ocean. Technol., 34, 2283–2293, 2017.
Bowman, M. J., Kibblewhite, A. C., Chiswell, S. M., and Murtagh, R.: Shelf fronts and tidal stirring in Greater Cook Strait, New Zealand, Oceanol. Ac., 6, 119–129, 1983.
Bryden, H. L. and Nurser, A. G.: Effects of strait mixing on ocean stratification, J. Phys. Oceanogr., 33, 1870–1872, 2003.
Dale, A. C. and Inall, M. E.: Tidal mixing processes amid small-scale, deep-ocean topography, Geophys. Res. Lett., 42, 484–491, https://doi.org/10.1002/2014GL062755, 2015.
Dillon, T. M.: Vertical overturns: A comparison of Thorpe and Ozmidov length scales, J. Geophys. Res.-Ocean., 87, 9601–9613, 1982.
Dunckley, J. F., Koseff, J. R., Steinbuck, J. V., Monismith, S. G., and Genin, A.: Comparison of mixing efficiency and vertical diffusivity models from temperature microstructure, J. Geophys. Res., 117, C10008, https://doi.org/10.1029/2012JC007967, 2012.
Finnigan, T. D., Luther, D. S., and Lukas, R.: Observations of enhanced diapycnal mixing near the Hawaiian Ridge, J. Phys. Oceanogr., 32, 2988–3002, 2002.
Forrest, B. M., Gardner, J., and Taylor, M. D.: Internal borders for managing invasive marine species, J. Appl. Ecol., 46, 46–54, 2009.
Frants, M., Damerell, G. M., Gille, S. T., Heywood, K. J., MacKinnon, J., and Sprintall, J.: An assessment of density-based finescale methods for estimating diapycnal diffusivity in the Southern Ocean, J. Atmos. Ocean. Technol., 30, 2647–2661, 2013.
Gregg, M. C. and Özsoy, E.: Flow, water mass changes, and hydraulics in the Bosphorus, J. Geophys. Res.-Ocean., 107, 1–23, https://doi.org/10.1029/2000JC000485, 2002.
Heath, R. A.: Semidiurnal tides in Cook Strait, New Zeal. J. Mar. Fresh., 12, 87–97, 1978.
Helfrich, K. R.: Time-dependent two-layer hydraulic exchange flows, J. Phys. Oceanogr., 25, 359–373, 1995.
Hogg, A. M., Ivey, G. N., and Winters, K. B.: Hydraulics and mixing in controlled exchange flows, J. Geophys. Res.-Ocean., 106, 959–972, 2001.
Imberger, J. and Boashash, B.: Application of the Wigner-Ville distribution to temperature gradient microstructure: A new technique to study small-scale variations, J. Phys. Oceanogr., 16, 1997–2012, 1986.
Jarosz, E., Teague, W. J., Book, J. W., and Beşiktepe, Ş.: On flow variability in the Bosphorus Strait, J. Geophys. Res.-Ocean., 116, 1–17, https://doi.org/10.1029/2010JC00686, 2011.
Koch-Larrouy, A., Atmadipoera, A., Van Beek, P., Madec, G., Aucan, J., Lyard, F., Grelet, J., and Souhaut, M.: Estimates of tidal mixing in the Indonesian archipelago from multidisciplinary INDOMIX in-situ data, Deep-Sea Res. Pt. I, 106, 136–153, 2015.
Lafuente, J. G., Pozas, E. B., Garrido, J. C. S., Sannino, G., and Sammartino, S.: The interface mixing layer and the tidal dynamics at the eastern part of the Strait of Gibraltar, J. Mar. Syst., 117, 31–42, 2013.
Lu, Y., Lueck, R. G., and Huang, D.: Turbulence characteristics in a tidal channel, J. Phys. Oceanogr., 30, 855–867, 2000.
Lueck, R. G., Wolk, F., and Yamazaki, H.: Oceanic velocity microstructure measurements in the 20th century, J. Oceanogr., 58, 153–174, 2002.
Macoun, P. and Lueck, R.: Modeling the spatial response of the airfoil shear probe using different sized probes, J. Atmos. Ocean. Technol., 21, 284–297, 2004.
Mashayek, A., Caulfield, C. P., and Peltier, W. R.: Time-dependent, non-monotonic mixing in stratified turbulent shear flows: Implications for oceanographic estimates of buoyancy flux, J. Fluid Mechan., 736, 570–593, 2013.
Mater, B. D. and Venayagamoorthy, S. K.: A unifying framework for parameterizing stably stratified shear-flow turbulence, Phys. Fluids, 26, 036601, https://doi.org/10.1063/1.4868142, 2014.
Mater, B. D., Schaad, S. M., and Venayagamoorthy, S. K.: Relevance of the Thorpe length scale in stably stratified turbulence, Phys. Fluids, 25, 076604, https://doi.org/10.1063/1.4813809, 2013.
Mater, B. D., Venayagamoorthy, S. K., St. Laurent, L., and Moum, J. N.: Biases in Thorpe-scale estimates of turbulence dissipation, Part I: Assessments from large-scale overturns in oceanographic data, J. Phys. Oceanogr., 45, 2497–2521, 2015.
Scott, B. E., Sharples, J., Ross, O. N., Wang, J., Pierce, G. J., and Camphuysen, C. J.: Sub-surface hotspots in shallow seas: fine-scale limited locations of top predator foraging habitat indicated by tidal mixing and sub-surface chlorophyll, Mar. Ecol.-Prog. Ser., 408, 207–226, 2010.
Scotti, A.: Biases in Thorpe-scale estimates of turbulence dissipation, Part II: energetics arguments and turbulence simulations, J. Phys. Oceanogr., 45, 2522–2543, 2015.
Smyth, W. D., Moum, J. N., and Caldwell, D. R.: The efficiency of mixing in turbulent patches: Inferences from direct simulations and microstructure observations, J. Phys. Oceanogr., 31, 1969–1992, 2001.
Stevens, C.: Residual flows in Cook Strait, a large tidally dominated strait, J. Phys. Oceanogr., 44, 1654–1670, 2014.
Stevens, C. L., Smith, M. J. Grant, B., Stewart, C. L., and Divett, T.: Tidal stream energy extraction in a large deep strait: the Karori Rip, Cook Strait, Cont. Shelf Res., 33, 100–109, 2012.
Stewart, R. W. and Grant, H. L.: Early measurements of turbulence in the ocean: Motives and techniques, J. Atmos. Ocean. Technol., 16, 1467–1473, 1999.
St Laurent, L. C., Toole, J. M., and Schmitt, R. W.: Buoyancy forcing by turbulence above rough topography in the abyssal Brazil Basin, J. Phys. Oceanogr., 31, 3476–3495, 2001.
Tanaka, Y., Yasuda, I., Osafune, S., Tanaka, T., Nishioka, J., and Volkov, Y. N.: Internal tides and turbulent mixing observed in the Bussol Strait, Prog. Oceanogr., 126, 98–108, 2014.
Timmermans, M. L. and Winsor, P.: Scales of horizontal density structure in the Chukchi Sea surface layer, Cont. Shelf Res., 52, 39–45, 2013.
Toole, J. M., Schmitt, R. W., and Polzin, K. L.: Estimates of diapycnal mixing in the abyssal ocean, Science, 264, 1120–1123, 1994.
Waterhouse, A. F., MacKinnon, J. A., Nash, J. D., Alford, M. H., Kunze, E., Simmons, H. L., Polzin, K. L., St. Laurent, L. C., Sun, O. M., Pinkel, R., and Talley, L. D.: Global patterns of diapycnal mixing from measurements of the turbulent dissipation rate, J. Phys. Oceanogr., 44, 1854–1872, 2014.
Wesson, J. C. and M.C. Gregg: Mixing at Camarinal Sill in the Strait of Gibraltar, J. Geophys. Res., 99, 9847–9878, 1994.
Wolk, F., Yamazaki, H., Seuront, L., and Lueck, R. G.: A new free-fall profiler for measuring biophysical microstructure, J. Atmos. Ocean. Technol., 19, 780–793, 2002.