Technical note: Two types of absolute dynamic ocean topography
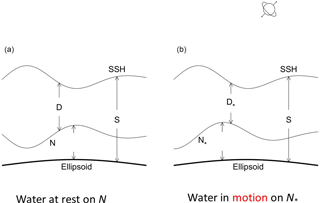
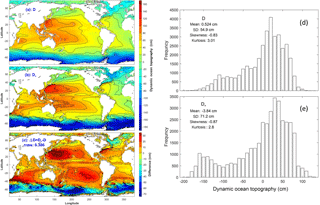
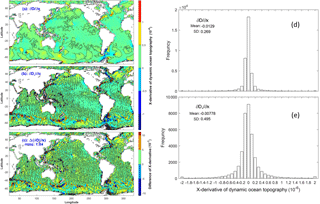
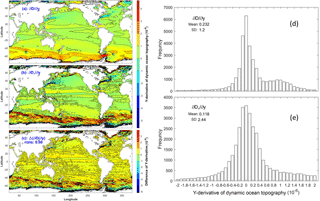
Two types of marine geoid exist with the first type being the average level of sea surface height (SSH) if the water is at rest (classical definition), and the second type being satellite-determined with the condition that the water is usually not at rest. The differences between the two are exclusion (inclusion) of the gravity anomaly and non-measurable (measurable) in the first (second) type. The associated absolute dynamic ocean topography (referred to as DOT), i.e., SSH minus marine geoid, correspondingly also has two types. Horizontal gradients of the first type of DOT represent the absolute surface geostrophic currents due to water being at rest on the first type of marine geoid. Horizontal gradients of the second type of DOT represent the surface geostrophic currents relative to flow on the second type of marine geoid. Difference between the two is quantitatively identified in this technical note through comparison between the first type of DOT and the mean second type of DOT (MDOT). The first type of DOT is determined by a physical principle that the geostrophic balance takes the minimum energy state. Based on that, a new elliptic equation is derived for the first type of DOT. The continuation of geoid from land to ocean leads to an inhomogeneous Dirichlet boundary condition with the boundary values taking the satellite-observed second type of MDOT. This well-posed elliptic equation is integrated numerically on 1∘ grids for the world oceans with the forcing function computed from the World Ocean Atlas (T, S) fields and the sea-floor topography obtained from the ETOPO5 model of NOAA. Between the first type of DOT and the second type of MDOT, the relative root-mean square (RRMS) difference (versus RMS of the first type of DOT) is 38.6 % and the RMS difference in the horizontal gradients (versus RMS of the horizontal gradient of the first type of DOT) is near 100 %. The standard deviation of horizontal gradients is nearly twice larger for the second type (satellite-determined marine geoid with gravity anomaly) than for the first type (geostrophic balance without gravity anomaly). Such a difference needs further attention from oceanographic and geodetic communities, especially the oceanographic representation of the horizontal gradients of the second type of MDOT (not the absolute surface geostrophic currents).