the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evaluation of nonidentical versus identical twin approaches for observation impact assessments: an ensemble-Kalman-filter-based ocean assimilation application for the Gulf of Mexico
Katja Fennel
Bin Wang
Arnaud Laurent
Keith R. Thompson
Lynn K. Shay
Assessments of ocean data assimilation (DA) systems and observing system design experiments typically rely on identical or nonidentical twin experiments. The identical twin approach has been recognized as yielding biased impact assessments in atmospheric predictions, but these shortcomings are not sufficiently appreciated for oceanic DA applications. Here we present the first direct comparison of the nonidentical and identical twin approaches in an ocean DA application. We assess the assimilation impact for both approaches in a DA system for the Gulf of Mexico that uses the ensemble Kalman filter. Our comparisons show that, despite a reasonable error growth rate in both approaches, the identical twin produces a biased skill assessment, overestimating the improvement from assimilating sea surface height and sea surface temperature observations while underestimating the value of assimilating temperature and salinity profiles. Such biases can lead to an undervaluation of some observing assets (in this case profilers) and thus a misguided distribution of observing system investments.
Ocean data assimilation (DA), i.e., the incorporation of observations into ocean models to obtain the best possible estimate of the ocean state, has become standard practice for improving the accuracy of model predictions and reanalyses. Benefiting from the rapid expansion of ocean observing platforms and advances in computing power, various ocean DA applications at both regional and global scales have been developed in support of ocean hindcasts, nowcasts, and forecasts (see, e.g., recent reviews in Moore et al., 2019 and Fennel et al., 2019). Necessarily, the credibility of a DA system demands rigorous validation. It is straightforward to assess the assimilation impact (i.e., the differences between ocean state estimates from a model run with and without assimilation), whereby a better fit of the model state to observations following assimilation might be considered positive. But in practice, the value of such an assessment is limited because it either does not consider independent observations (i.e., observations that have not been assimilated into the system) or has to reduce the quantity of the data used for assimilation when reserving some for independent assessment.
An alternative assessment approach is to conduct twin experiments (e.g., Anderson et al., 1996; Halliwell et al., 2014). The essential steps of a twin experiment are to (1) predefine a simulation as the “truth”, (2) sample synthetic observations from this truth, (3) assimilate these observations into a different simulation referred to as the forecast run, and (4) assess the skill of this assimilative run against a non-assimilative (“free”) run using independent observations sampled from the truth. If the chosen truth and forecast runs are from same model implementation but with perturbed initial, forcing or boundary conditions, the method is referred to as the “identical twin” approach. If two different model types are used, we refer to the method as the “nonidentical twin” approach. We note that the intermediate approach in which the same model type is employed but with sufficiently different configurations (e.g., different physical parameterizations and/or spatial resolution) is conventionally termed the fraternal twin (Halliwell et al., 2014). In addition to validating DA systems, twin experiments are used for observing system simulation experiments (OSSEs) that evaluate the impact of different ocean observing system designs on predictive skill (e.g., Oke and O'Kane, 2011; Halliwell et al., 2015, 2017). Ideally, the truth and forecast simulations in the twin system used for the OSSE should be from two different models; i.e., they should be nonidentical twins.
The identical twin approach has been more commonly used in oceanic DA applications (e.g., Counillon and Bertino, 2009b; Simon and Bertino, 2009; Srinivasan et al., 2011; Song et al, 2016a; Yu et al., 2018a) although it is well known from atmospheric OSSEs that this approach provides biased impact assessments when the error growth rate between the truth and forecast runs is insufficient (e.g., Arnold and Dey, 1986; Atlas, 1997; Hoffman and Atlas, 2016). This fact is not yet sufficiently recognized in applications of ocean OSSEs and skill assessments of oceanic DA systems (Halliwell et al., 2014). To avoid the potential bias in impact assessments associated with identical twin experiments, Halliwell et al. (2014) proposed applying a criterion that has long been used in realistic atmospheric OSSEs. They suggested that the model for the forecast run should be configured differently enough from that for the truth run so that the rate of error growth between them has the same magnitude as that between state-of-the-art ocean models and the true ocean. They also suggested comparing the assimilation impact in the twin framework with that in a realistic configuration; if a similar impact is obtained in both twin and realistic configurations, the twin DA framework can be considered appropriate for assessing assimilation impact and conducting OSSEs. Fraternal OSSEs have proven instructive for evaluating the assimilation impact of different observing platforms in the Gulf of Mexico (Halliwell et al., 2015) and North Atlantic (Halliwell et al., 2017).
However, a direct comparison of fraternal or nonidentical and identical twin approaches has not yet been conducted for an ocean application to the best of our knowledge. Motivated by this, we use an ocean DA system for the Gulf of Mexico (GOM) to compare and contrast the nonidentical and identical twin approaches in an assimilation impact assessment. The rationale for choosing the GOM as our test bed is that the nondeterministic aspects of the circulation in the GOM, including the northward penetration of Loop Current (LC) intrusions and the associated eddy shedding, require DA for accurately hindcasting and forecasting the circulation. The need for accurate nowcasts and predictions was particularly acute during the 2010 Deepwater Horizon (DwH) oil spill. Previous data assimilation applications in the GOM have focused primarily on improvements of the surface current fields observable from satellites or drifters but did not examine the assimilation impact on subsurface flow fields. As the DwH oil spill has shown, knowledge of model skill in simulating the subsurface circulation is also important. Utilizing twin experiments, we aim to examine the assimilation impact on the subsurface circulation.
Toward this objective we implement an advanced ensemble DA technique, the ensemble Kalman filter (EnKF), for a high-resolution (horizontal resolution of 5 km) model covering the entire GOM. The EnKF utilizes flow-dependent background error covariances in contrast to the time-invariant covariance in optimal-interpolation- (OI) or variational-based DA systems that have previously been used in the GOM (e.g., Counillon and Bertino, 2009a, b; Jacobs et al., 2014). By rigorously assessing the skill of the EnKF-based assimilative model (with an emphasis on the subsurface fields) through nonidentical and identical twin experiments and OSSEs, we demonstrate how the identical twin approach yields misleading conclusions in this practical application. We also address whether an improved skill in reproducing the surface dynamics of the LC and associated eddies translates into improved skill in simulating the subsurface circulation.
2.1 Physical model
The model is configured using the Regional Ocean Modelling System (Haidvogel et al., 2008; ROMS, http://myroms.org, last access: 16 June 2016) for the GOM (Fig. 1a). It has a horizontal resolution of 5 km and 36 terrain-following vertical layers with higher resolution near the surface and bottom. Vertical turbulent mixing is parameterized using the Mellor and Yamada (1982) level 2.5 closure scheme, and bottom friction is specified using a quadratic drag formulation. The model utilizes a 3rd-order accurate, non-oscillatory advection scheme for tracers (HSIMT; Wu and Zhu, 2010), which is mass-conservative and positive–definite with low dissipation and no overshooting, and it is forced with the atmospheric forcing fields from the European Centre for Medium-Range Weather Forecasts (ECMWF) (https://apps.ecmwf.int/datasets/, last access: 15 April 2018). River input is prescribed as in Xue et al. (2013), with daily runoff from the US Geological Survey for rivers inside the US and long-term climatological estimates for rivers in Mexico and Cuba. The model is one-way nested inside the 1∕12∘ data-assimilative global Hybrid Coordinate Ocean Model (HYCOM) (Chassignet et al., 2009). Tidal forcing is neglected because tides are small in the GOM.
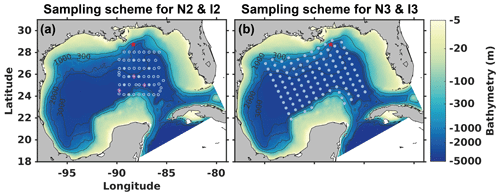
Figure 1Model domain and bathymetry. The red star denotes the location of the DwH oil rig. (a) Sampling scheme for twin experiments N2 and I2. The symbols represent stations where temperature (circles) and salinity (magenta diamonds) profiles were collected by Shay et al. (2011), with deep temperature or salinity profiles (down to 1000 m) marked as filled circles or magenta diamonds and shallow temperature profiles (down to 400 m) as open circles. (b) Sampling scheme for N3 and I3. The dots represent stations where temperature and salinity profiles extending to 1000 m of depth were sampled from the “truth” run.
Previous studies have highlighted two important aspects for model skill in the GOM: a sufficiently high horizontal resolution for representing the mesoscale dynamics (e.g., Chassignet et al., 2005) and an accurate representation of the LC inflow through the Straits of Yucatán (e.g., Oey et al., 2003). Our model meets the two requirements. The 5 km horizontal resolution is sufficient to resolve mesoscale processes (the baroclinic Rossby radius is 30 to 40 km in the central GOM; see Oey et al., 2005), and our ROMS model is nested in a data-assimilative HYCOM model that simulates an accurate structure of the LC and its eddies. Initial model–data comparisons showed that the model has skill in statistically simulating the main features of the LC intrusion, with a slight overestimation of its northward penetration during the simulation period (Yu, 2018).
2.2 Experimental framework
The deterministic formulation of the EnKF (DEnKF), first introduced by Sakov and Oke (2008), was implemented in the GOM model. The DEnKF has been successfully used in previous ocean assimilation applications (e.g., Simon et al., 2015; Jones et al., 2016; Yu et al., 2018a). The algorithm consists of sequential forecast and analysis steps, wherein the model ensemble is propagated forward in time during the forecast step and updated with available observations using the Kalman filter analysis equation during the analysis step. The analysis equation is given as
where x is the n×1 model state estimate vector (n is the number of model state variables at all grid points), the superscripts a and f represent the analysis and the forecast estimates, respectively, d is the m×1 vector of observations (m is the number of available observations), H is the linear m×n measurement operator mapping the model state onto the observations, and K is the n×m Kalman gain matrix given as
Pf is the n×n forecast error covariance matrix (approximated by the forecast ensemble), R is the m×m observation error covariance, and T denotes the matrix transpose. Different from the traditional EnKF (Burgers et al., 1998), which requires perturbing observations to obtain an analysis error covariance consistent with that given by the Kalman filter, the DEnKF updates the ensemble mean using the analysis in Eq. (1) and ensemble anomalies with the same equation but half the Kalman gain K without perturbing observations; it is hence termed “deterministic”. Details on the DEnKF derivation and implementation can be found in Sakov and Oke (2008).
2.2.1 Nonidentical twin experiments
In nonidentical twin experiments, the truth is generated by interpolating the daily outputs of the 1∕12∘ data-assimilative global HYCOM (Chassignet et al., 2009) onto the ROMS model grid. Synthetic observations are sampled from the truth, including sea surface height (SSH), sea surface temperature (SST), and temperature and salinity profiles. Typical Gaussian observation errors of N(0, 2 cm) for SSH, N(0, 0.3 ∘C) for temperature (both SST and temperature profiles), and N(0, 0.01) for salinity are added to the sampled data. SSH and SST are sampled weekly at every fifth horizontal grid point to yield a spatial resolution of ∘ as such an assimilation time window or spatial resolution has been adopted in previous realistic DA applications (e.g., weekly gridded product of SSH used in Moore et al., 2011, and Song et al., 2016b; weekly gridded product of SST in Hoteit et al., 2013). SSH in regions shallower than 300 m is not used for assimilation because dynamics in shelf areas where wind and buoyancy forcing dominate could substantially deviate from the geostrophic state, weakening the correlation between SSH and subsurface temperature and salinity fields. For SST, only regions shallower than 10 m are excluded. Importantly when preparing the synthetic SSH observations, the mean dynamic topography (MDT) of the HYCOM truth run had to be removed from the sampled SSH data, and the MDT of the ROMS model had to be added. The MDTs of the HYCOM and ROMS models were obtained by averaging their respective daily SSH outputs from 2010 to 2016.
Temperature and salinity profiles were sampled with two different sampling schemes (see locations in Fig. 1a, b). The first scheme adopts the sampling dates and locations used in the survey described in Shay et al. (2011). The key features of this scheme are that the sampling is centered on the LC region, the majority (363 out of 472) of temperature profiles are limited to the upper 400 m, and very few (34) salinity profiles were collected. In the second scheme, coverage was extended such that temperature and salinity profiles are sampled simultaneously over the entire central GOM down to 1000 m of depth on 23 instead of 9 dates.
A non-assimilative run, subsequently referred to as the free run, is initialized on 1 April 2010 from the global HYCOM and compared with the data-assimilative runs to evaluate the impact of the assimilation.
In the DA experiments, 20-member ensembles are started from different initial conditions and forced by perturbed boundary conditions and wind fields. The initial conditions were created by using three-dimensional (3-D) fields from daily HYCOM outputs within a 20 d window centered on the initialization date of 1 April 2010. The boundary conditions were generated by applying a time lag of up to ±10 d to the boundary condition (i.e., the first member's boundary conditions are 10 d ahead) following Counillon and Bertino (2009b). The perturbed wind fields were created by first conducting an empirical orthogonal function (EOF) decomposition of the wind field and then adding perturbations from the mixture of the first four EOF modes to the wind field, whereby the four perturbation modes were multiplied with zero-mean unit-variance random numbers and a scale factor of 0.5 similar to Thacker et al. (2012) and Li et al. (2016).
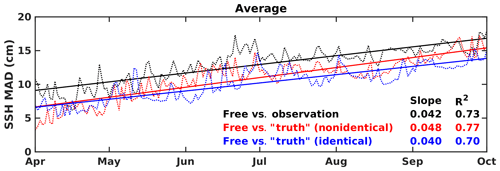
Figure 2Time series of MAD error (cm) averaged over the open gulf (excluding shelf regions shallower than 300 m) for the free run SSH relative to the SSH from the satellite observation (black dashed line), the “truth” in the nonidentical (red) and identical (blue) twin experiments, respectively. The corresponding colored solid lines are linear regressions of the time series, wherein the slope values represent the respective MAD error growth rate (cm d−1).
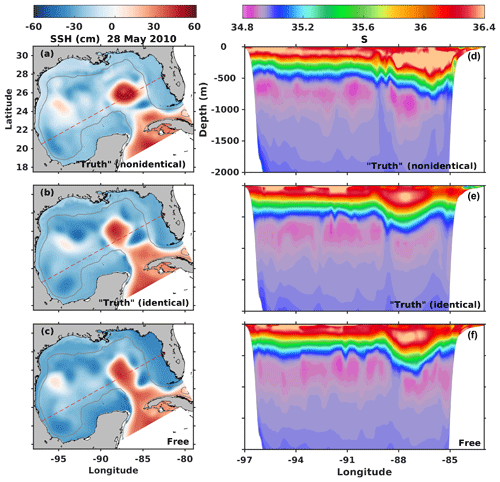
Figure 3Sea surface height (SSH, cm) and transect of salinity (S) on 28 May 2010. Panels (a) and (d) are from HYCOM and used as the “truth” in the nonidentical twin experiments. Panels (b) and (e) are from ROMS and used as the truth in identical twin experiments. Panels (c) and (f) are from the free ROMS run. The gray contour in the SSH maps marks the bathymetric depth of 300 m, and the red dashed line shows the position of the transect in panels (d)–(f).
We used an ensemble of 20 as it was the largest size feasible given the computing resources available to us and found this to work well in our application. The same ensemble size has also been used in previous studies (e.g., Hu et al., 2012; Mattern et al., 2013). Distance-based localization with an influence radius of 50 km was applied as described in Evensen (2003) to prevent the potential negative effects of spurious correlations between distant grid points. An inflation factor of 1.05 was applied to the ensemble anomalies, inflating the ensemble spread around its mean at every assimilation step as introduced by Anderson and Anderson (1999). This accounts for the potential underestimation of the forecast error covariance due to the small ensemble size. The choice of localization radius and inflation factor is based on initial tests and takes into account the fact that the baroclinic Rossby radius in the central GOM is 30 to 40 km (Oey et al., 2005) to avoid choosing a localization radius value that is too small.
Observations are assimilated weekly from 2 April to 3 September 2010, updating the 3-D temperature and salinity fields. On each assimilation date, the observations (regardless of observation type) are assimilated simultaneously in one single step. After the last assimilation step on 3 September 2010, the ensemble is run without any data assimilation for 4 more weeks. Three assimilation experiments (referred to as N1, N2, and N3) are conducted. N1 assimilates weekly SSH and SST, while N2 and N3 assimilate the temperature and salinity profiles following the two sampling schemes described earlier (Fig. 1a, b) in addition to SSH and SST. Model–data misfit is quantified by computing the mean absolute deviations (MADs), i.e., the average of the absolute deviations, of model simulations from the truth for the open gulf (defined as regions deeper than 300 m). That is, , where and N is the number of data pairs. For ensemble assimilation runs, the forecast ensemble mean at assimilation steps is used for calculating the MAD.
2.2.2 Identical twin experiments
The identical twin experiments have a similar setup as the nonidentical twin experiments except that the truth is not taken from HYCOM but generated from a ROMS simulation that differs from the free run only in its initial and boundary conditions and wind forcing. The truth run is started on 1 April 2010 from an initial state from an earlier ROMS simulation and is forced with boundary conditions that are lagging behind those of the free run by 14 d and wind fields reconstructed from the first 10 EOFs of the realistic ECMWF wind. Since the same model architecture is used in the free and truth runs for the identical twin, there is no need to correct MDT when sampling SSH observations.
Similar to the nonidentical twin setup, three assimilation experiments are conducted in the identical twin framework (I1, I2, and I3) that assimilate the same combinations of observations as in N1, N2, and N3.
3.1 Assessment of the nonidentical and identical twin experiment setup
We first examine the credibility of the nonidentical and identical twin setups by comparing the error growth rates in SSH between the free run and the truth for both twins (Fig. 2). The nonidentical twin has a slightly higher error growth rate (0.048 cm d−1) than the identical twin (0.040 cm d−1), but both are of a similar magnitude as that between the free run and real observations (0.042 cm d−1). This meets the requirement suggested by Halliwell et al. (2014) that the errors between the free run and the truth should grow at a similar rate as errors that develop between state-of-the-art ocean models and the true ocean. The comparison in Fig. 3 also shows that differences between the truth and free runs in SSH and subsurface salinity fields are obvious and qualitatively comparable between the nonidentical and identical twin experiments. This satisfies the other requirements suggested in Halliwell et al. (2014), namely that the free run is able to reproduce the main features of the simulated phenomenon (i.e., the LC intrusion) with some realism and that there are sufficient differences between the free and truth runs for the assimilation method to correct.
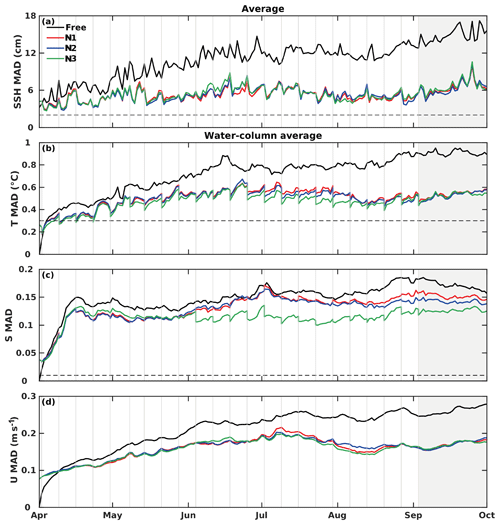
Figure 4Time series of MAD averaged over the open gulf (excluding shelf regions shallower than 300 m) for (a) SSH (cm), (b) temperature (T, ∘), (c) salinity (S), and (d) velocity (U, m s−1) from the free run and nonidentical twin runs. The MADs of all physical variables except SSH were averaged over the entire water column. Black dashed lines in (a), (b), and (c)denote the values of observation errors. Gray vertical lines indicate the assimilation steps. The gray area marks the 4-week period without data assimilation.
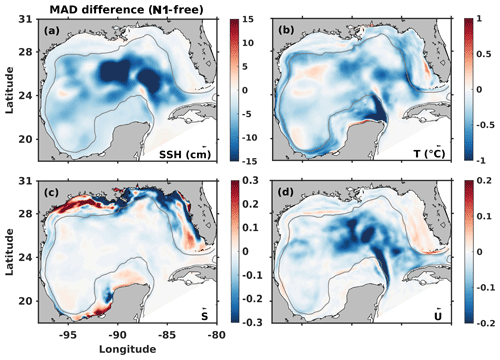
Figure 5The difference in physical variable time-averaged (daily snapshots from 1 April to 1 October) MAD between nonidentical twin N1 and the free run. MADs of temperature and velocity were averaged over the entire water column. Negative values (cold colors) correspond to a decrease in MAD compared to the free run, whereas positive values (warm colors) correspond to an increase. The gray contour marks the bathymetric depth of 300 m.
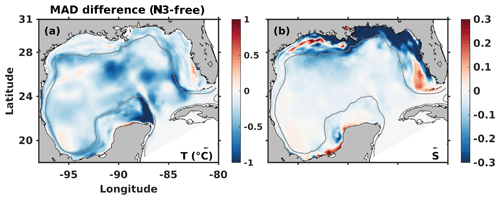
Figure 6The difference in physical variable time- and water-column-averaged (daily snapshots from 1 April to 1 October) MAD between nonidentical twin N3 and the free run. Negative values (cold colors) correspond to a decrease in MAD compared to the free run, whereas positive values (warm colors) correspond to an increase. The gray contour marks the bathymetric depth of 300 m.
3.2 Impact of assimilation in nonidentical twin experiments
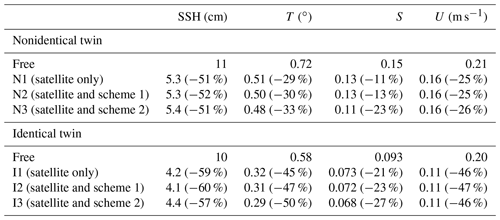
Temporally and spatially averaged MADs between the nonidentical twin assimilation runs and the free run are summarized in Table 1 (temporal evolution is shown in Fig. 4). Assimilating SSH and SST in N1 significantly reduces the MADs of SSH (by 51 %) as well as temperature (by 29 %) and velocity fields (by 25 %), and it slightly reduces the MADs in salinity (by 11 %) (Table 1). After the last assimilation step, MADs remain low for at least 4 weeks (Fig. 4). Assimilating additional temperature and salinity profiles (in N2 and N3) further benefits temperature and especially salinity fields, in particular in N3 for which the salinity MAD is reduced by 23 %, but has almost no effect on SSH and velocity MAD.
Table 1Mean absolute deviation (MAD) from the “truth” of physical variables for free and data assimilation runs in nonidentical twin and identical experiments. The MADs were averaged over all grid cells excluding the shelves (defined by water depths <300 m) and daily snapshots from 1 April to 1 October 2010. At assimilation steps the forecast ensemble mean was used for the calculation. The percentage change relative to the free run is presented in parentheses.
In N1 the MAD in the SSH, temperature, and velocity components is reduced for almost the entire domain, with the most significant reductions in the LC region (Fig. 5). The reduction in salinity MAD is relatively small in N1 but larger in N3 for which additional temperature and salinity profiles are assimilated (Fig. 6). In contrast to SSH, temperature, and velocity, the biggest impact of assimilation on the salinity field is on the shelf where salinity is more variable than in the open gulf because of river inputs.
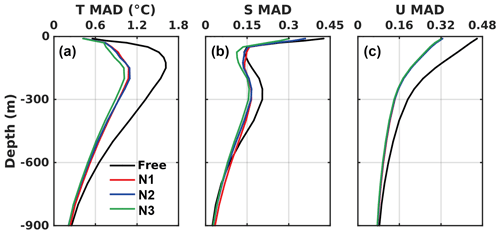
Figure 7Profiles of MAD averaged over the open gulf (excluding shelf regions shallower than 300 m) and daily snapshots from 1 April to 1 October 2010 for (a) temperature (T, ∘), (b) salinity (S), and (c) velocity (U, m s−1) from the free run and the nonidentical twin runs.
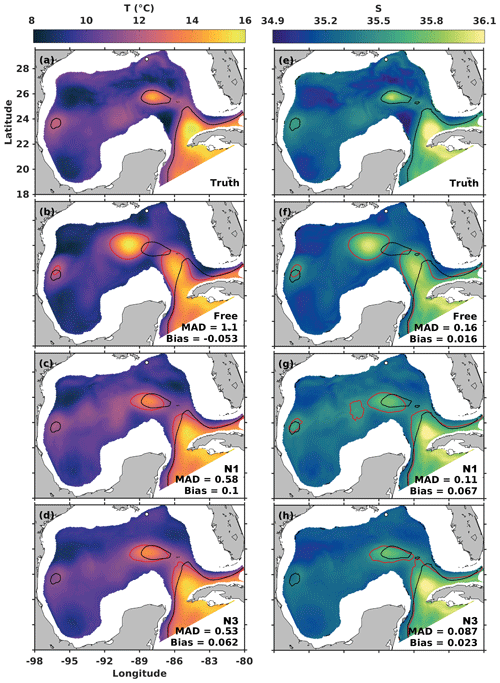
Figure 8August mean (a, b, c, d) temperature (T, ∘) and (e, f, g, h) salinity (S) at 400 m from the “truth”, free, N1, and N3 run in nonidentical twin experiments. The white dot denotes the location of the Deepwater Horizon oil rig. The contours mark the 12∘ isotherm and 35.5 isohaline, respectively; the black contours denote the isotherm or isohaline for the truth, while red contours denote those for the actual simulation in each panel. The horizontal domain-averaged MAD and bias values at 400 m for each experiment relative to the truth are also presented in the respective panels.
Vertically, the reductions of spatially and temporally averaged MAD extend to nearly 900 m of depth for temperature and velocity and 500 m for salinity (Fig. 7). The maximum reductions in MAD amount to 0.6∘ for temperature at 200 m, 0.12 for surface salinity, and 0.07 m s−1 for surface velocity (Fig. 7). Assimilating temperature and salinity profiles in N3 leads to greater reductions of temperature and salinity MAD, primarily in the upper 300 m, compared to N1.
Next, we assess the impact of assimilation on subsurface temperature and salinity fields (Fig. 8). The “true” spatial distribution of mean temperature and salinity at 400 m of depth in August shows only a weak northward intrusion of warm and salty LC water and a detached anticyclonic eddy. Compared to the truth, the free run overestimates the northward extension of the LC (depicted by the 12∘ isotherm and 35.5 isohaline), and the detached eddy is misaligned. Assimilation corrects the extension and angle of the LC and the position of the eddy, significantly reducing the averaged MAD error by 47 % and 31 % for temperature and salinity, respectively, in the N1 run and 52 % and 46 % for those in the N3 run.
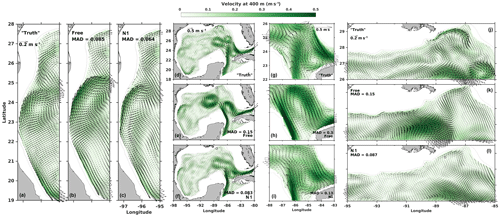
Figure 9August mean velocity at 400 m in the (a, d, g, j) “truth”, (b, e, h, k) free, and (c, f, i, l) N1 run in nonidentical twin experiments. Panels in the first, third, and fourth columns are zoomed into the western shelf, central gulf, and northern shelf, respectively. The white dot denotes the location of the DwH oil rig, and gray contours mark the bathymetric depths of 300, 1000, 2000, and 3000 m, respectively.
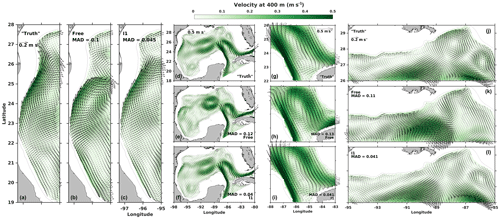
Figure 10August mean velocity at 400 m in the (a, d, g, j) “truth”, (b, e, h, k) free, and (c, f, i, l) I1 run in identical twin experiments. Panels in the first, third, and fourth columns are zoomed into the western shelf, central gulf, and northern shelf, respectively. The white dot denotes the location of the DwH oil rig, and gray contours mark the bathymetric depths of 300, 1000, 2000, and 3000 m, respectively.
Lastly, we examine the assimilation impact on subsurface circulation in a comparison of August mean circulation at 400 m of depth for the nonidentical twin runs (Fig. 9). The truth shows a limited northeastward extension of the LC with two eddies shedding (Fig. 9d). As already mentioned above, the free run overestimates the northward extension and simulates a more energetic detached anticyclonic eddy that has propagated further west (Fig. 9e). Assimilation in N1 brings the simulated shape, strength, and location of the LC and LC eddies closer to the truth with an overall MAD reduction of ∼45 % compared to the free run (Fig. 9f). A closer look at the LC intrusion region (Fig. 9g, h, i) and the western (Fig. 9a, b, c) and northern shelf breaks (Fig. 9j, k, l) shows that the greatest improvement in subsurface circulation is in the open gulf and LC region where mesoscale processes dominate (MAD reduction of ∼57 %), whereas the improvement in circulation is weaker along the shelf regions where submesoscale processes are important and the influences of the open ocean, bathymetry, and local wind and river forcing coexist (MAD reductions of ∼25 % and ∼42 % on the western and northern shelf, respectively). Specifically, the small-scale currents surrounding the spill site observed in the truth (i.e., the strong anticyclonic eddy to the east of the spill site and cyclonic eddy to its southwest) are not satisfactorily represented in either the free run or N1. The results of N2 and N3 are very similar to N1.
3.3 Assimilation impact in identical versus nonidentical twins
Assimilating SSH and SST in identical twin I1 leads to even larger error reductions than in the nonidentical twin N1, with domain-averaged MAD reductions in temperature of 45 %, salinity of 21 %, and velocity fields of 46 % relative to 29 %, 11 %, and 25 %, respectively, in the nonidentical twin N1 (Table 1). However, the benefit of assimilating additional temperature and salinity profiles in I2 and I3 for temperature and salinity fields in the identical twin framework is much smaller than in the nonidentical twin (Table 1).
With respect to the simulated subsurface circulation, the improvement by assimilating SSH and SST is also much greater in identical twin I1 (Fig. 10) than in nonidentical twin N1, with a MAD reduction of ∼67 % versus ∼45 %. In addition, a remarkable improvement in subsurface circulation following assimilation in I1 is observed not only in the LC intrusion region (MAD reduction of ∼69 %) but also on the shelves (∼55 % and ∼63 %, respectively, on the western and northern shelves), including the region near the DwH spill site (Fig. 10).
We implemented the EnKF technique in a high-resolution regional model for the GOM. The skill of this data-assimilative system was assessed through a series of nonidentical and identical twin experiments assimilating data from different observing system configurations. The differences between the two approaches have important implications for observing system design studies.
Consistent with previous assimilation studies in the GOM (e.g., Wang et al., 2003; Counillon and Bertino, 2009b; Hoteit et al., 2013), our nonidentical and identical twin experiments both show that assimilating altimetry data can constrain a range of large-scale to mesoscale features such as the LC and associated eddies. The warmer and more saline LC and its eddies have a temperature and salinity signature that is distinct from the so-called Gulf Common Water and have a clear signal of elevated SSH. The assimilation of SSH using the multivariate EnKF can therefore adjust temperature and salinity profiles based on the SSH information. The assimilation of SSH and SST substantially corrects the subsurface temperature, salinity, and velocity fields from the surface to depths of up to 900 m, with clear improvements in the location and intensity of the LC and LC eddies.
The nonidentical twin experiments show that salinity is less constrained than temperature when assimilating only SSH and SST. The assimilation of additional temperature profiles (experiment N2) only slightly improves salinity; the inclusion of salinity profiles (experiment N3) is more effective in improving salinity. This highlights the value of assimilating salinity profiles to constrain model salinity fields. The importance of salinity measurements has also been reported in the realistic DA configuration by Halliwell et al. (2015). However, such additional benefits of assimilating temperature and salinity profiles for model-simulated temperature and salinity fields are not observed in the identical twin experiments, which already yield much greater improvements when assimilating SSH and SST alone. It follows that the additional information content in the subsurface observations (i.e., profiles) within the identical twin system is much smaller than that for the nonidentical twin. We attribute this to the lack of intrinsic difference in the identical twin (e.g., physical model parameterizations, spatial resolution) between the truth and forecast model runs, making it easier to correct the subsurface model fields by assimilating SSH and SST alone. This close agreement of subsurface fields between the forecast model and truth necessarily reduces the additional information content of subsurface observations during assimilation.
Another major difference between the nonidentical and identical twin approaches lies in the assimilation impact on subsurface circulation. In the nonidentical twin experiments, assimilating satellite altimetry effectively constrains the large-scale to mesoscale structures on the order of 100 km that dominate the deep GOM. The improved circulation in the deep GOM has a positive but relatively limited impact on the circulation near the DwH spill site, which is located in the transition zone between the open gulf (where the circulation is dominated by the mesoscale LC and its eddies) and the shelf (where currents are largely driven by wind and density forcing). The assimilation of SSH, SST, and additional temperature and salinity profiles (the spatial distance between profiles in the experiment N3 is ∼70 km) in our nonidentical twin experiments provides limited constraints on the small-scale circulation features in this region. This is consistent with Wang et al. (2003), who found that assimilating SSH and SST could not accurately resolve smaller-scale eddies in the DeSoto Canyon region near the DwH site. It has been suggested previously that higher-resolution localized observations (Lin et al., 2007; Jacobs et al., 2014; Carrier et al., 2014; Berta et al., 2015; Muscarella et al., 2015) and even finer model resolution (< 5 km; Ledwell et al., 2016) are needed to better constrain these submesoscale features. In contrast to the nonidentical twin, the identical twin I1, which assimilates only SSH and SST, yields remarkable improvements not only in the mesoscale circulation dominating the open GOM but also the smaller-scale processes prevailing along the shelf breaks, including the DeSoto Canyon region where the spill site is located. This is largely because in the identical twin setup, the intrinsic model structures (e.g., subgrid-scale parameterizations, horizontal and vertical resolution) for the truth and forecast model runs are identical so that an improvement in large-scale processes due to the assimilation of SSH and SST can readily translate to an improvement in the simulated subgrid-scale processes.
These results provide two examples of how the identical twin approach yields misleading impact assessments: (1) the improvement in subsurface fields resulting from assimilating SSH and SST is overestimated, and (2) the value of additional profiles is underestimated. Undervaluing the information provided by a class of observational assets is particularly troublesome in the context of OSSEs. While this issue is well known in the context of atmospheric OSSEs (e.g., Arnold and Dey, 1986; Atlas, 1997; Hoffman and Atlas, 2016), it is not yet sufficiently recognized for ocean OSSEs and skill assessments of oceanic DA systems. The Halliwell et al. (2014) set of design criteria and evaluation procedures for ocean OSSEs serves as guidance for designing twin experiments for a data-assimilative system. Their main criteria include the following: (1) the rate of error growth between simulated and observed states must be similar between the twin framework and reality, and (2) the assimilation impact in the twin framework should be comparable to that of a realistic configuration assimilating actual observations. We found a similar rate of error growth in SSH in both twin experiments and in reality, and the impact of assimilation in the nonidentical twin experiment is found to be very similar to that in a realistic assimilation configuration presented in Yu (2018). Thus, our direct comparisons of an identical versus nonidentical twin not only lend support to the recommendation of using the nonidentical over the identical twin approach, but also hint that assessing error growth in just one ocean property is insufficient. Additional criteria, such as a comparative assessment of skill between twin and realistic assimilation configurations as described in Halliwell et al. (2014), are needed to obtain a more credible impact assessment from the twin framework.
We presented a direct comparison of nonidentical and identical twin approaches for assessing data assimilation impact in an EnKF-based ocean DA system for the Gulf of Mexico. To the best of our knowledge, this is the first direct comparison of nonidentical and identical twin approaches for an oceanic DA system and first demonstration of how the identical twin approach can yield misleading assessments in practice. Our comparisons show that the identical twin approach overestimates the improvement in model skill resulting from assimilating SSH and SST, including for the subsurface circulation, while underestimating the value of additional information from temperature and salinity profiles. In the context of observing system design, such biased assessments are problematic and can lead to misguided decisions on balancing investments between different observing assets. We conclude that skill assessments and OSSEs from identical twin experiments should be avoided or, at least, regarded with caution. While the nonidentical twin approach is more robust, questions remain about how to best choose a credible framework. In our case, the rate of error growth in SSH alone appears to have been an insufficient criterion.
The ROMS model code can be accessed at http://www.myroms.com (Haidvogel et al., 2008) (last access: 16 June 2016). ROMS data assimilation model outputs are publicly available through the Gulf of Mexico Research Initiative Information & Data Cooperative (GRIIDC) at https://doi.org/10.7266/n7-zc10-mz49 (Yu et al., 2018b). HYCOM data can be downloaded at http://tds.hycom.org/thredds/catalog.html (Chassignet et al., 2009) (last access: 9 July 2019).
LY and KF conceived the study. LY carried out the model simulations and analysis. BW assisted in preparing the HYCOM data and validating the free model run. AL, KRT, and LKS provided inputs to the model setup and data assimilation techniques. LY and KF discussed the results and wrote the paper with contributions from all coauthors.
The authors declare that they have no conflict of interest.
Data are publicly available through the Gulf of Mexico Research Initiative Information & Data Cooperative (GRIIDC) at https://data.gulfresearchinitiative.org/data/R5.x275.000:0009 (last access: 18 December 2019). Liuqian Yu acknowledges support from the Nova Scotia Graduate Fellowship program. The authors would like to thank two anonymous referees for their constructive comments.
This research was made possible in part by a grant from the Gulf of Mexico Research Initiative (GoMRI-V-487). This work used the Extreme Science and Engineering Discovery Environment (XSede) Comet at the San Diego Supercomputer Center through allocation (TG-OCE170001).
This paper was edited by Eric J. M. Delhez and reviewed by two anonymous referees.
Anderson, D. L. T., Sheinbaum, J., and Haines, K.: Data assimilation in ocean models, Rep. Prog. Phys., 59, 1209–1266, 1996.
Anderson, J. L. and Anderson, S. L.: A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts, Mon. Weather Rev., 127, 2741–2758, https://doi.org/10.1175/1520-0493(1999)127<2741:AMCIOT>2.0.CO;2, 1999.
Arnold, C. P. and Dey, C. H.: Observing-Systems Simulation Experiments?: Past, Present, and Future, Bull. Am. Meteorol. Soc., 67, 687–695, 1986.
Atlas, R.: Atmospheric observations and experiments to assess their usefulness in data assimilation, J. Meteorol. Soc. Japan, 75, 111–130, 1997.
Burgers, G., van Leeuwen, J. P., and Evensen, G.: Analysis scheme in the Ensemble Kalman Filter, Mon. Weather Rev., 126, 1719–1724 https://doi.org/10.1175/1520-0493(1998)126<1719:ASITEK>2.0.CO;2, 1998.
Berta, M., Griffa, A., Magaldi, M. G., Ozgokmen, T. M., Poje, A. C., Haza, A. C., and Josefina Olascoaga, M.: Improved surface velocity and trajectory estimates in the Gulf of Mexico from blended satellite altimetry and drifter data, J. Atmos. Ocean Tech., 32, 1880–1901, https://doi.org/10.1175/JTECH-D-14-00226.1, 2015.
Carrier, M. J., Ngodock, H., Smith, S., and Jacobs, G.: Impact of assimilating ocean velocity observations inferred from Lagrangian drifter data using the NCOM-4DVAR, Mon. Weather Rev., 142, 1509–1524, https://doi.org/10.1175/MWR-D-13-00236.1, 2014.
Chassignet, E. P., Hurlburt, H. E., Smedstad, O. M., Barron, C. N., Ko, D. S., Rhodes, R. C., Shriver, J. F., Wallcraft, A. J., and Arnone, R.: Assessment of data assimilative ocean models in the Gulf of Mexico using ocean color, in: Circulation in the Gulf of Mexico: Observations and Models, edited by: Sturges, W. and Lugo-Fernández, A., Geophysical Monograph Series (Vol. 161, pp. 87–100), American Geophysical Union, Washington, DC, 2005.
Chassignet, E. P., Hurlburt, H. E., Metzger, E. J., Smedstad, O., Cummings, J., Halliwell, G., Bleck, R., Baraille, R., Wallcraft, A. J., Lozano, C., Tolman, H. L., Srinivasan, A., Hankin, S., Cornillon, P., Weisberg, R., Barth, A., He, R., Werner, F., and Wilkin, J.: US GODAE: Global ocean prediction with the HYbrid Coordinate Ocean Model (HYCOM), Oceanography, 22, 64–75, https://doi.org/10.5670/oceanog.2009.39, 2009.
Counillon, F. and Bertino, L.: Ensemble Optimal Interpolation: Multivariate properties in the Gulf of Mexico, Tellus A, 61, 296–308, https://doi.org/10.1111/j.1600-0870.2008.00383.x, 2009a.
Counillon, F. and Bertino, L.: High-resolution ensemble forecasting for the Gulf of Mexico eddies and fronts, Ocean Dynam., 59, 83–95, https://doi.org/10.1007/s10236-008-0167-0, 2009b.
Evensen, G.: The Ensemble Kalman Filter: Theoretical formulation and practical implementation, Ocean Dynam., 53, 343–367, https://doi.org/10.1007/s10236-003-0036-9, 2003.
Fennel, K., Gehlen, M., Brasseur, P., Brown, C. W., Ciavatta, S., Cossarini, G., Crise, A., Edwards, C. A., Ford, D., Friedrichs, M. A. M., Gregoire, M., Jones, E., Kim, H.-C., Lamouroux, J., Murtugudde, R., and Perruche, C.: Advancing Marine Biogeochemical and Ecosystem Reanalyses and Forecasts as Tools for Monitoring and Managing Ecosystem Health, Front. Mar. Sci., 6, 1–9, https://doi.org/10.3389/fmars.2019.00089, 2019.
Haidvogel, D. B., Arango, H., Budgell, W. P., Cornuelle, B. D., Curchitser, E., Di Lorenzo, E., Fennel, K., Geyer, W. R., Hermann, A. J., Lanerolle, L., Levin, J., McWilliams, J. C., Miller, A. J., Moore, A. M., Powell, T. M., Shchepetkin, A. F., Sherwood, C. R., Signell, R. P., Warner, J. C., and Wilkin, J.: Ocean forecasting in terrain-following coordinates: formulation and skill assessment of the regional ocean modeling system, J. Comput. Phys., 227, 3595–3624, 2008.
Halliwell, G. R., Srinivasan, A., Kourafalou, V., Yang, H., Willey, D., Le Hénaff, M., and Atlas, R.: Rigorous evaluation of a fraternal twin ocean OSSE system for the open Gulf of Mexico, J. Atmos. Ocean Tech., 31, 105–130, https://doi.org/10.1175/JTECH-D-13-00011.1, 2014.
Halliwell, G. R., Kourafalou, V., Le Hénaff, M., Shay, L. K., and Atlas, R.: OSSE impact analysis of airborne ocean surveys for improving upper-ocean dynamical and thermodynamical forecasts in the Gulf of Mexico, Prog. Oceanogr., 130, 32–46, https://doi.org/10.1016/j.pocean.2014.09.004, 2015.
Halliwell, G. R., Mehari, M. F., Le Hénaff, M., Kourafalou, V. H., Androulidakis, I. S., Kang, H. S., and Atlas, R.: North Atlantic Ocean OSSE system: Evaluation of operational ocean observing system components and supplemental seasonal observations for potentially improving tropical cyclone prediction in coupled systems, J. Oper. Oceanogr., 10, 154–175, https://doi.org/10.1080/1755876X.2017.1322770, 2017.
Hoffman, R. N. and Atlas, R.: Future observing system simulation experiments, B. Am. Meteorol. Soc., 97, 1601–1616, https://doi.org/10.1175/BAMS-D-15-00200.1, 2016.
Hoteit, I., Hoar, T., Gopalakrishnan, G., Collins, N., Anderson, J., Cornuelle, B., Kohl, A., and Heimbach, P.: A MITgcm/DART ensemble analysis and prediction system with application to the Gulf of Mexico, Dynam. Atmos. Oceans, 63, 1–23, https://doi.org/10.1016/j.dynatmoce.2013.03.002, 2013.
Hu, J., Fennel, K., Mattern, J. P., and Wilkin, J.: Data assimilation with a local Ensemble Kalman Filter applied to a three-dimensional biological model of the Middle Atlantic Bight, J. Marine Syst., 94, 145–156, https://doi.org/10.1016/j.jmarsys.2011.11.016, 2012.
Jacobs, G. A., Bartels, B. P., Bogucki, D. J., Beron-Vera, F. J., Chen, S. S., Coelho, E. F., Curcic, M., Griffa, A., Gough, M., Haus, B. K., Haza, A. C., Helber, R. W., Hogan, P. J., Huntley, H. S., Iskandarani, M., Judt, F., Kirwan, A. D., Laxague, N., Valle-Levinson, A., Lipphardt, B. L., Mariano, J. A., Ngodock, H. E., Novelli, G., Olascoaga, M. J., Özgökmen, T. M., Poje, A. C., Reniers, A. J. H. M., Rowley, C. D., Ryan, E. H., Smith, S. R., Spence, P. L., Thoppil, P. G., and Wei, M.: Data assimilation considerations for improved ocean predictability during the Gulf of Mexico Grand Lagrangian Deployment (GLAD), Ocean Model., 83, 98–117, https://doi.org/10.1016/j.ocemod.2014.09.003, 2014.
Jones, E. M., Baird, M. E., Mongin, M., Parslow, J., Skerratt, J., Lovell, J., Margvelashvili, N., Matear, R. J., Wild-Allen, K., Robson, B., Rizwi, F., Oke, P., King, E., Schroeder, T., Steven, A., and Taylor, J.: Use of remote-sensing reflectance to constrain a data assimilating marine biogeochemical model of the Great Barrier Reef, Biogeosciences, 13, 6441–6469, https://doi.org/10.5194/bg-13-6441-2016, 2016.
Ledwell, J. R., He, R., Xue, Z., DiMarco, S. F., Spencer, L. J., and Chapman, P.: Dispersion of a tracer in the deep Gulf of Mexico, J. Geophys. Res.-Oceans, 121, 1110–1132, https://doi.org/10.1002/2015JC011405, 2016.
Li, G., Iskandarani, M., Hénaff, M. L., Winokur, J., Le Maître, O. P., and Knio, O. M.: Quantifying initial and wind forcing uncertainties in the Gulf of Mexico, Comput. Geosci., 20, 1133–1153, https://doi.org/10.1007/s10596-016-9581-4, 2016.
Lin, X. H., Oey, L. Y., and Wang, D. P.: Altimetry and drifter data assimilations of loop current and eddies, J. Geophys. Res.-Oceans, 112, 1–24, https://doi.org/10.1029/2006JC003779, 2007.
Mattern, J. P., Dowd, M., and Fennel, K.: Particle filter-based data assimilation for a three-dimensional biological ocean model and satellite observations, J. Geophys. Res.-Oceans, 118, 2746–2760, https://doi.org/10.1002/jgrc.20213, 2013.
Mellor, G. L. and Yamada, T.: Development of a turbulence closure model for geophysical fluid problems, Rev. Geophys., 20, 851–875, 1982.
Moore, A. M., Arango, H. G., Broquet, G., Edwards, C. A., Veneziani, M., Powell, B. S., Foley, D., Doyle, J., Costa, D., and Robinson, P.: The regional ocean modeling system (ROMS) 4-dimensional variational data assimilation systems, Part II: performance and application to the california current system, Prog. Oceanogr., 91, 50–73, 2011.
Moore, A. M., Martin, M. J., Akella, S., Arango, H. G., Balmaseda, M., Bertino, L., Ciavatta, S., Cornuelle, B., Cummings, J., Frolov, S., Lermusiaux, P., Oddo, P., Oke, P. R., Storto, A., Teruzzi, A., Vidard, A., and Weaver, A.: Synthesis of ocean observations using data assimilation for operational, real-time and reanalysis systems: a more complete picture of the state of the ocean, Front. Mar. Sci., 6, 90, https://doi.org/10.3389/fmars.2019.00090, 2019.
Muscarella, P., Carrier, M. J., Ngodock, H., Smith, S., Lipphardt, B. L., Kirwan, A. D., and Huntley, H. S.: Do assimilated drifter velocities improve Lagrangian predictability in an operational ocean model?, Mon. Weather Rev., 143, 1822–1832, https://doi.org/10.1175/MWR-D-14-00164.1, 2015.
Oey, L.-Y., Lee, H.-C., and Schmitz Jr., W. J.: Effects of winds and Caribbean eddies on the frequency of Loop Current eddy shedding: A numerical model study, J. Geophys. Res.-Oceans, 108, 3324. https://doi.org/10.1029/2002JC001698, 2003.
Oey, L.-Y., Ezer, T., and Lee, H.-C.: Loop Current, rings and related circulation in the Gulf of Mexico: a review of numerical models and future challenges, in: Circulation in the Gulf of Mexico: Observations and Models, edited by: Sturges, W. and Lugo-Fernández, A., Geophysical Monograph Series (Vol. 161, pp. 87–100), American Geophysical Union, Washington, DC, 2005.
Oke, P. R. and O'Kane, T. J. (Eds.): Observing system design and assessment. Operational Oceanography in the 21st Century, Springer, Netherlands, 123–151, 2011.
Sakov, P. and Oke, P. R.: A deterministic formulation of the ensemble Kalman filter: an alternative to ensemble square root filters, Tellus A, 60, 361–371, https://doi.org/10.1111/j.1600-0870.2007.00299.x, 2008.
Shay, L. K., Jaimes, B., Brewster, J. K., Meyers, P., McCaskill, E. C., Uhlhorn, E., Marks, F., Halliwell Jr., G. R., Smedstad, O. M., and Hogan, P.: Airborne ocean surveys of the Loop Current complex from NOAA WP-3D in support of the Deepwater Horizon oil spill, in: Monitoring and Modeling the Deepwater Horizon Oil Spill: A Record-Breaking Enterprise, edited by: Liu, Y., Macfadyen, A., Ji, Z.-G., and Weisberg, R. H., Geophysical Monograph Series (Vol. 195, pp. 131-152), American Geophysical Union, Washington, DC, https://doi.org/10.1029/2011GM001101, 2011.
Simon, E. and Bertino, L.: Application of the Gaussian anamorphosis to assimilation in a 3-D coupled physical-ecosystem model of the North Atlantic with the EnKF: a twin experiment, Ocean Sci., 5, 495–510, https://doi.org/10.5194/os-5-495-2009, 2009.
Simon, E., Samuelsen, A., Bertino, L., and Mouysset, S.: Experiences in multiyear combined state-parameter estimation with an ecosystem model of the North Atlantic and Arctic Oceans using the Ensemble Kalman Filter, J. Mar. Syst., 152, 1–17, https://doi.org/10.1016/j.jmarsys.2015.07.004, 2015.
Song, H., Edwards, C. A., Moore, A. M., and Fiechter, J.: Data assimilation in a coupled physical-biogeochemical model of the California Current System using an incremental lognormal 4-dimensional variational approach: Part 2-Joint physical and biological data ssimilation twin experiments, Ocean Model., 106, 146–158, https://doi.org/10.1016/j.ocemod.2016.04.001, 2016a.
Song, H., Edwards, C. A., Moore, A. M., and Fiechter, J.: Data assimilation in a coupled physical–biogeochemical model of the California Current System using an incremental lognormal 4-dimensional variational approach: part 3 – assimilation in a realistic context using satellite and in situ observations, Ocean Model., 106, 159–172, https://doi.org/10.1016/j.ocemod.2016.04.001, 2016b.
Srinivasan, A., Chassignet, E. P., Bertino, L., Brankart, J.-M., Brasseur, P., Chin, T. M., Counillon, F., Cummings, J. A., Mariano, A. J., Smedstad, O. M., and Thacker, W. C.: A comparison of sequential assimilation schemes for ocean prediction with the HYbrid Coordinate Ocean Model (HYCOM): Twin experiments with static forecast error covariances, Ocean Model., 37, 85–111, https://doi.org/10.1016/j.ocemod.2011.01.006, 2011.
Thacker, W. C., Srinivasan, A., Iskandarani, M., Knio, O. M., and Hénaff, M. L.: Propagating boundary uncertainties using polynomial expansions, Ocean Model., 43–44, 52–63, https://doi.org/10.1016/j.ocemod.2011.11.011, 2012.
Wang, D.-P., Oey, L.-Y., Ezer, T., and Hamilton, P.: Near-surface currents in DeSoto Canyon (1997–99): comparison of current meters, satellite observation, and model simulation, J. Phys. Oceanogr., 33, 313–326, https://doi.org/10.1175/1520-0485(2003)033<0313:NSCIDC>2.0.CO;2, 2003.
Wu, H. and Zhu, J.: Advection scheme with 3rd high-order spatial interpolation at the middle temporal level and its application to saltwater intrusion in the Changjiang Estuary, Ocean Model., 33, 33–51, https://doi.org/10.1016/j.ocemod.2009.12.001, 2010.
Yu, L.: Improved prediction of the effects of anthropogenic stressors in the Gulf of Mexico through regional-scale numerical modelling and data assimilation, Ph.D. thesis, Dalhousie University, Canada, http://hdl.handle.net/10222/75005 (last access: 18 December 2019), 2018.
Yu, L., Fennel, K., Bertino, L., El, M., and Thompson, K. R.: Insights on multivariate updates of physical and biogeochemical ocean variables using an Ensemble Kalman Filter and an idealized model of upwelling, Ocean Model., 126, 13–28, https://doi.org/10.1016/j.ocemod.2018.04.005, 2018a.
Yu, L., Fennel, K., Wang, B., Laurent, A., Thompson, K. R., and Shay, L. K.: Gulf of Mexico regional ocean model at 5 km horizontal resolution assimilating satellite and float data with Ensemble Kalman Filter (EnKF) from 2010-04-01 to 2010-10-01, Distributed by: Gulf of Mexico Research Initiative Information and Data Cooperative (GRIIDC), Harte Research Institute, Texas A&M University-Corpus Christi, https://doi.org/10.7266/n7-zc10-mz49, 2018b.
Xue, Z., He, R., Fennel, K., Cai, W.-J., Lohrenz, S., and Hopkinson, C.: Modeling ocean circulation and biogeochemical variability in the Gulf of Mexico, Biogeosciences, 10, 7219–7234, https://doi.org/10.5194/bg-10-7219-2013, 2013.





