the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A multiscale ocean data assimilation approach combining spatial and spectral localisation
Ann-Sophie Tissier
Jean-Michel Brankart
Charles-Emmanuel Testut
Giovanni Ruggiero
Emmanuel Cosme
Pierre Brasseur
Ocean data assimilation systems encompass a wide range of scales that are difficult to control simultaneously using partial observation networks. All scales are not observable by all observation systems, which is not easily taken into account in current ocean operational systems. The main reason for this difficulty is that the error covariance matrices are usually assumed to be local (e.g. using a localisation algorithm in ensemble data assimilation systems), so that the large-scale patterns are removed from the error statistics.
To better exploit the observational information available for all scales in the assimilation systems of the Copernicus Marine Environment Monitoring Service, we investigate a new method to introduce scale separation in the assimilation scheme.
The method is based on a spectral transformation of the assimilation problem and consists in carrying out the analysis with spectral localisation for the large scales and spatial localisation for the residual scales. The target is to improve the observational update of the large-scale components of the signal by an explicit observational constraint applied directly on the large scales and to restrict the use of spatial localisation to the small-scale components of the signal.
To evaluate our method, twin experiments are carried out with synthetic altimetry observations (simulating the Jason tracks), assimilated in a model configuration of the North Atlantic and the Nordic Seas.
Results show that the transformation to the spectral domain and the spectral localisation provides consistent ensemble estimates of the state of the system (in the spectral domain or after backward transformation to the spatial domain). Combined with spatial localisation for the residual scales, the new scheme is able to provide a reliable ensemble update for all scales, with improved accuracy for the large scale; and the performance of the system can be checked explicitly and separately for all scales in the assimilation system.
Over the last decades, the spectral window of the oceanic processes observed from space has steadily increased. At the same time, model resolution has also improved to better understand and interpret the observed signals. This progress in observations and models is a challenge for ensemble data assimilation because the size of the ensemble is always very small compared to the number of degrees of freedom to be monitored. The model is usually too expensive to perform large-size ensemble simulations. This means that the probability distribution of the possible states of ocean is described by a small sample as compared to the dimension of the subspace over which uncertainties develop. In particular, the rank of the ensemble covariance matrix is much smaller than the rank of the real error covariance matrix. A traditional approximation to solve this problem is to localise this error covariance matrix (Houtekamer and Mitchell, 1998; Hamill et al., 2001; Testut et al., 2003; Brankart et al., 2011). The analysis is then applied locally by only using observations within a defined radius of influence which is bound to decrease with the broadening of the spectral window controlled by the data assimilation. The control of large scales, namely larger than this radius of influence, thus results from the combination of a large number of local analyses.
The large-scale structures, although they are well observed (in the ocean by altimetry, ARGO floats, etc.), are therefore only indirectly controlled by the algorithm. Observations simultaneously contain information about small-scale structures (especially at the observation point) and about larger-scale structures, taking into account the full observational network. Spatial localisation does not directly take advantage of each scale contained in the observations system.
Because of the limited size of the ensemble, it is difficult to explicitly control the full range of scales without separating the spectral components of the signal. Separation of scales during the analysis step of data assimilation algorithms allows us to adjust localisation according to the considered spectral band of the signal. This is helpful to directly control the large scales which are frequently and precisely observed (altimetry, ARGO floats, etc.). To separate scales in data assimilation, two approaches have been previously studied: the multiscale filter and the spectral transformation. The multiscale filter consists in separating the signal in two spectral bands, delimited by a cutting scale, in order to achieve two distinct ensemble analysis in the spatial domain (Zhou et al., 2008; Zhang et al., 2009). In this scheme, applied to an ensemble Kalman filter (EnKF), two distinct localisation windows are used to exploit correlations over a longer distance for the analysis of the large scales. A more approximate version has also been proposed by simply combining the increments obtained for each of the two spectral bands (Miyoshi and Kondo, 2013). A comparable approach was proposed for 3D-Var systems by Li et al. (2015). Alternatively, Buehner (2012) proposed a spectral transformation approach within an ensemble-variational (EnVar) system, which is a spatial and a spectral localisation with a wavelet transform. This method is more generic because scales are separated continuously from the largest scales to the smallest scales. Localisation is used to neglect the correlations between the components of the signal which are distant both in terms of spatial location and in terms of scales. However, this method would be expensive for large systems and could be difficult to insert in a global ocean assimilation system. More recently, Buehner and Shlyaeva (2015) and Caron and Buehner (2018) have developed a new formulation of this algorithm for EnVar systems. It incorporates the multiscale filter idea of decomposing the signal in several spectral bands and it avoids the complete removal of the between-scale covariances (Buehner and Charron, 2007). This formulation makes use of an augmented spatial/spectral ensemble covariance matrix, whereas the result of the analysis is still computed in the spatial domain.
Following a similar idea of combining the multiscale filter and spectral transformation approaches, we propose in the present paper to combine these two algorithms by applying a spectral analysis with spectral localisation (hereinafter called spectral localisation) to the large-scale components of the signal and a spatial analysis with spatial localisation (hereinafter called spatial localisation) for the residual scales. By separating the components, we avoid using an augmented covariance matrix, and we thus potentially neglect useful statistical relationships. However, this makes the multiscale system less expensive and easier to implement in an existing ensemble data assimilation system. It is indeed expected that the spectral transformation of the large scales is cheap enough to be applied to a large-size global ocean system, and that spectral localisation is more appropriate than spatial localisation to capture the large-scale components of the observed signal. On the other hand, for the small-scale components, the spectral transformation becomes too expensive, and the local correlation structure prevails. The target is thus to improve the observational update of the large-scale components of the signal by an explicit observational constraint applied directly on the large scales and to restrict the use of spatial localisation to the residual-scale components of the signal. These analyses should be done one after the other to be included in an existing sequential algorithm as operated, for instance, by Mercator Océan.
The performance of this multiscale observational update is then studied with an example application in the context of Copernicus Marine Environment Monitoring Service (CMEMS) systems. We performed a 70-member ensemble simulation using the oceanic model NEMO (Nucleus for European Modelling of the Ocean; Madec, 2008) version 3.6 at with the CREG4 configuration (Dupont et al., 2015) as part of the CMEMS project. This configuration of the North Atlantic and Nordic Seas is currently used at Mercator Océan for developing and testing the future assimilation system. This configuration is thus appropriate to check that our new algorithm can be integrated in the data assimilation system of Mercator Océan (SAM2) used for the CMEMS programme.
The objective of this paper is to describe the multiscale observational update algorithm that we have developed and to evaluate its performance using the CREG4 ensemble system. The paper is organised as follows. In Sect. 2, we present the practical problem that we want to solve: we describe the prior ensemble, the observation system and the difficulties associated with the multiscale correlation structure. In Sect. 3, we present the spectral transformation that is applied in this study to better display the multiscale correlation structure. In Sect. 4, we present the algorithm that we have developed to make better use of the correlation structure for all scales. In Sect. 5, we evaluate the resulting algorithm using the application problem described in Sect. 2. This is done by studying the reliability and resolution of the updated ensemble for each wavelength of the control variables.
The purpose of this section is to introduce the example application that is used in this paper to study the performance of the multiscale observational update. This example application is chosen to serve the development of the CMEMS systems and to display the multivariate character of the assimilation problem. The model configuration and the prior ensemble simulation are described in Sect. 2.1; the assimilation problem is described in Sect. 2.2; and the multiscale character of the ensemble correlation structure is described in Sect. 2.3.
2.1 Ensemble model simulation
Our example application is based on a resolution model of the North Atlantic and the Nordic Seas. We used the oceanic model NEMO (Madec, 2008) version 3.6, with the CREG4 configuration as part of the CMEMS project. NEMO, used by a large community, is developed by European institutes and is used by the majority of the CMEMS stakeholders. It is a primitive equation model which computes the following prognostic variables: 3-D velocities, sea surface height, salinity and temperature. ERA-Interim reanalysis data, produced at ECMWF (Dee et al., 2011), are used for the atmospheric forcing. CREG4 is a realistic configuration for the North Atlantic and the Nordic Seas at the horizontal resolution. This configuration is described in the work of Dupont et al. (2015), except that we use a version instead of the nominal resolution. It has been developed by Environment Canada and coupled with Mercator Océan's SAM2 data assimilation system. The aim was to build a realistic description of the mean state and variability in the North Atlantic and the Nordic Seas. The CREG4 configuration is currently used by Mercator Océan and its resolution is sufficient to evaluate the multiscale assimilation algorithm; therefore, we use it for our study.
Uncertainties in the model are explicitly simulated using the standard NEMO stochastic parameterisation module developed by Brankart et al. (2015). The aim is to produce an ensemble with a sufficient spread for all variables, especially for the observed variables, all over the domain. This technique has been used to simulate six different kinds of uncertainties in the model as described in Table 1. Concerning the equation of state, we used the stochastic parameterisation proposed in Brankart (2013). The two standard deviation values given in the table correspond to the standard deviation of the random walks in the horizontal and the vertical directions. Uncertainties in air–sea fluxes are parameterised using a multiplicative noise (with gamma pdf to make it positive) applied to the turbulent exchange coefficients simulated by NEMO following the algorithm from Large and Yeager (2009) extended to other parameters (and evaluated by Mercator Océan). Ice uncertainties are parameterised using stochastic processes representing uncertainties in ice strength, ice albedo, ice/sea and ice/air drag coefficients.
Table 1Simulation of model uncertainties to perform the 70-member ensemble. It follows the working configuration used at Mercator Océan to perform ensembles for research and development in the context of CMEMS systems.
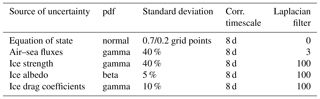
The standard deviation of the equation of state is defined according to longitude and latitude.
With this stochastic modelling system, a 70-member ensemble simulation, without assimilation, is performed for the 8-month period between mid-January and mid-September 2011. It will be used to perform the analyses in the present paper. This ensemble simulation yields a probability distribution for the evolution of the system, in particular the ensemble mean, hereafter 〈xf〉, where 〈⋅〉 indicates an ensemble mean over the members of the ensemble and the background error covariance matrix of the prior ensemble, Pf. Figure 1a and b show, respectively, the ensemble mean (〈xf〉) and the standard deviation of the prior ensemble. This ensemble is appropriate to illustrate the multiscale analysis in our study. Indeed, as will be shown later, the spread of the ensemble spans a wide range of scales from basin scale to mesoscale. Large scales as well as small structures are well represented, which will allow us to evaluate our separation scale algorithm. Nevertheless, the standard deviation is too small in the regions of strong eddy activity such as the Gulf Stream. This is mainly due to the model configuration (CREG4), which causes an excessive dissipation of the turbulent kinetic energy. Moreover, the variability is too large close to the East Siberian Sea. However, since we are using twin experiments, the simulation does not need to be perfectly realistic to evaluate our approach (providing that the multiscale nature of the problem remains). These characteristics are thus not likely to affect the evaluation of the multiscale algorithm that is performed in this study.
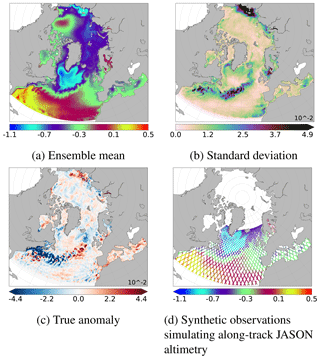
Figure 1SSH (in metres). Ensemble mean (a) and standard deviation (b) of the prior ensemble (N=69 members). The true anomaly (c) is defined as the difference between the true member (computed as an additional independent member of the ensemble) and the ensemble mean (a). Synthetic observations simulating along-track Jason altimetry (d) correspond to the true member along the track of the Jason altimeter plus a noise, following Eq. (1).
2.2 Definition of the twin experiments
The assimilation problem investigated in this study is based on twin experiments with altimetry. In this kind of experiment, the true state is known and synthetic observations are built from this true state. It is generated by the same model to which data assimilation is applied. This method has the advantage that the effectiveness of the different algorithms can be directly evaluated thanks to the known true state. One member of the ensemble simulation is left apart to be used as a reference (the simulated truth) from which the observations will be simulated: xtrue. The prior ensemble (indicated thereafter by the subscript f as forecast during an assimilation step) used in the experiments is thus a 69-member ensemble.
In this study, to illustrate the behaviour of the multiscale algorithm, we will concentrate on studying the observational update of the prior ensemble on 30 August 2011. Figure 1c shows the true anomaly: xtrue−〈xf〉. This true anomaly will be used as a reference to evaluate the effectiveness of the different localisation schemes and of the multiscale analysis. Synthetic observations are simulated by adding a simulated observational noise (ϵ: a Gaussian noise with 5 cm standard deviation) to the true state (xtrue) with the observation operator (H) along the track of the Jason altimeter:
In this experiment, a 10 d observation window is chosen to have the best coverage provided by Jason. Figure 1d shows the resulting synthetic observation of the sea surface height (SSH). The Jason altimeter does not provide any observation above 66∘ N latitude. In our example, there is thus no available observation to correct, during the analysis step, the large ensemble variance observed close to the East Siberian Sea (Fig. 1b). This is something that the multiscale approach will have to cope with.
The observational update of the prior ensemble will be performed with a square root algorithm. The analysis scheme used at Mercator Océan is derived from the singular evolutive extended Kalman filter (SEEK) (Pham et al., 1998; Brasseur and Verron, 2006), which is similar to that used in the ensemble transform Kalman filter (ETKF) (Bishop et al., 2001). It can be applied indifferently in the spatial domain as well as in the spectral domain. In the assimilation system, the observational update is usually applied to all model variables. In this paper, however, the effect of the multiscale approach will mainly be evaluated by the update of SSH, which is the observed variable, and by the update of temperature and salinity to illustrate the application of the method to non-observed variables. In the multiscale algorithm developed in this study, nothing will be changed in the core of the square root algorithm: the only novelty is that a spectral transformation is applied before the observational update to allow spectral localisation rather than spatial localisation. A spatial localisation scheme has been already developed and evaluated (Testut et al., 2003; Brankart et al., 2011). For this study, it has been adapted to be used in the spectral domain.
2.3 Ensemble correlation structure
The 69-member ensemble correlation structure (without the true state, which has been left apart) is illustrated in Fig. 2a and b. It has been computed according to two arbitrary reference points: one in the Gulf Stream and the other in the north-east Atlantic Ocean off the coast of Portugal. Ensemble correlation structure shows how the assimilation of an observation at this reference point will influence the other regions during the analysis step. For N=69 members, the correlation coefficient is significant at 95 % if it is larger in absolute value than 0.2367. In both examples, the most important and significant values, i.e. where the observation will have an impact, are mostly confined around the reference point. Some significant correlations are observed further, but their values are lower and not reliable enough to be used during an assimilation step. The usual solution to avoid the spurious effect of non-significant ensemble correlations is to perform a spatial localisation during the analysis step. It consists in completing the correlation structure provided by the ensemble by the assumption that only local correlations are significant and usable (Houtekamer and Mitchell, 1998; Hamill et al., 2001). The long-range correlations are thus assumed to be zero to perform the analysis step.
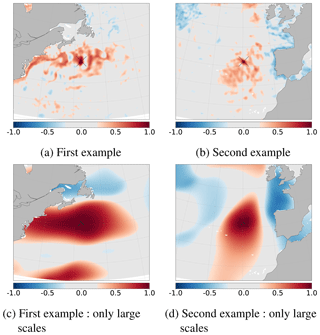
Figure 2Two examples of ensemble correlation for the prior ensemble (SSH), according to two different reference points indicated by black crosses, computed for the full spectrum (a, b) and for the large scales (c, d, , with lc=34 following Eqs. 2 and 3, which corresponds to a characteristic scale larger than L≈187 km). Light grey colour corresponds to non-significant values of ensemble correlations for an ensemble of N=69 members (smaller in absolute value than 0.2367 with significance threshold at 95 %).
However, if we look at the same correlation structure (from the same ensemble) for the large-scale component of the signal (characteristic scale larger than L≈187 km), as illustrated in Fig. 2c–d, we see that there are significant correlations over a much larger range. Hence, significant information of the large-scale signal is available even if the size of the ensemble is small. But these are usually masked by the presence of the small-scale signal. In the standard spatial localisation, these large-scale correlations structures are heavily suppressed and thus a part of the large-scale information is not used during the analysis step. The goal is now to find a way to correctly exploit these correlations in the assimilation scheme to better estimate the large-scale signal.
It seems difficult to explicitly control all scales of the system without separating the different spectral components of the signal. In this study, the main idea is to do a spectral transformation of all variables of the system in order to do the analysis in the spectral domain before going back in the spatial domain to do the next steps of the assimilation scheme.
The purpose of this section is to describe the linear transformation that will be applied on the state vectors and on the observation vectors to separate scales. The forward and backward transformations of the model data are described in Sect. 3.1 and 3.2, respectively; the transformation of observations and observation errors is described in Sect. 3.3; and the effect on the ensemble correlation structure is studied in Sect. 3.4.
3.1 Forward transformation: projection on the spherical harmonics
The forward transformation step involves transforming each input parameter used for the analysis into the spectral domain, namely each member of the prior ensemble, but also observations and observational errors. A full two-dimensional signal in spherical coordinates, f(θ, ϕ), can be projected on spherical harmonics Ylm(θ, ϕ) by the following spectral transformation (ST):
where l and m are the degree and order of each spherical harmonics, with l∈ℕ and . In principle, the integral in Eq. (2) extends over the whole sphere Ω. However, in the assimilation system, all fields f(θ, ϕ) that need to be transformed are anomalies with respect to the ensemble mean. In practice, it is thus possible to extend f(θ, ϕ) with zeroes outside the available domain ( on continents and outside the model domain) in order to compute the integral over the whole sphere. For a multivariate three-dimensional variable, this transformation can be applied to each vertical level of each model variable.
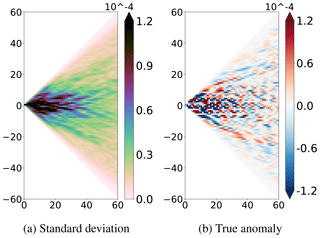
This spectral transformation provides a new point of view on the ensemble because it separates scales. Each degree l of the spherical harmonic indeed corresponds to a wavelength of a spherical harmonic , with Rc the Earth's radius, and thus to a characteristic scale . This reversible spectral transformation preserves the information for each degree l. The coefficients flm of the spherical harmonics decomposition can be computed for each degree l up to a selected degree l=lmax. This transformed field contains the same information, until lmax, as shown in the spatial domain in Fig. 1. The coefficients flm of each member of the prior ensemble have been computed for the SSH until the degree lmax=60, which corresponds to a wavelength λ≈667 km and a characteristic length L≈106 km. Figure 3a shows the standard deviation of this prior ensemble in the spectral domain. Figure 3b shows the result of the spectral transformation applied to the true SSH anomaly, i.e. the coefficients flm of the true SSH anomaly. Similar patterns have been observed by Wunsch and Stammer (1995) from early altimetric observations. Most of the variability is concentrated at large scales (small l). The variance becomes weak for meridional structures, i.e. for .
3.2 Backward transformation: scale separation
From the spectrum flm, the field can be reconstructed using the inverse transformation:
This inversion can be constrained to specific scales by choosing the values of lmin and lmax. The full field can be reconstructed since . This is how the method separates scales.
Any spectral band can thus be extracted by choosing the range [lmin; lmax] appropriately. Figure 4 shows the result of the extraction of the large scales applied to each member of the ensemble and to the true anomaly to keep only the large scales. In this case, lmin=0 and lmax=34, which corresponds to a wavelength λ≈1177 km and a characteristic scale L≈187 km. Small-scale structures have been properly removed and only large-scale structures remain visible on the figure.
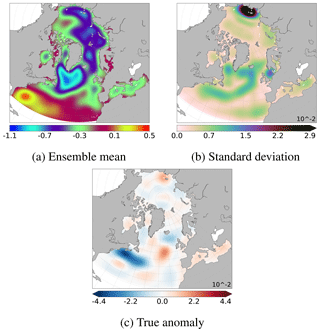
Figure 4Ensemble mean (a), standard deviation (b) of the prior ensemble and true anomaly (c) for the SSH (in metres), after extraction of the large scales (, with lc=34, which corresponds to a characteristic scale larger than L≈187 km; see Eq. 3).
The use of spherical harmonics is not the most natural way to separate scales for fields that do not extend over the whole sphere. In principle, it would, for instance, be better to use the eigenfunctions of the Laplacian operator defined for the model domain. They would account for the land barriers and would display a better relation to the system dynamics. However, they would also be much more expensive to compute than the spherical harmonics and would need to be stored and then loaded each time they are needed to separate scales. This is why we preferred using spherical harmonics in this study: they make the method numerically efficient and they are sufficient to obtain a relevant spectral decomposition of the input signal.
3.3 Transformation of the observations
In theory, transformation of observations is not needed to separate scales in the assimilation system. It should be sufficient to introduce the scale separation operator in the observation operator of the existing algorithm. However, for practical reasons, the algorithm that we are proposing requires a preprocessing of the observations to separate scales. This is done to keep the algorithm easy to implement in an existing system: nothing new needs to be implemented except the scale separation operator and to keep the resulting algorithm efficient enough to be applicable to a large-size assimilation system.
In this section, we show how this transformation of observations can be performed by regression of the observations on the spherical harmonics (see Sect. 3.3.1) and how the statistics of the observational errors can be transformed accordingly (see Sect. 3.3.2).
3.3.1 Regression of observations
For all observations that are not available on a regular grid (for which Eq. 2 could directly be applied), the spectral transformation can be performed by linear regression of the innovation vector (anomaly of the observations with respect to the ensemble mean) on the spherical harmonics.
The approach is to look for the spectral amplitudes flm so that the corresponding field f(θ, ϕ) (up to degree lmax following Eq. (3) with lmin=0) minimises the following distance to observations fo:
where p is the size of the observation vector (including bogus observations); is the observation at coordinates (θk, ϕk); is typically the observation error standard deviation (including the representativity error corresponding to the signal above degree lmax) at coordinates (θk, ϕk). If the observation system is insufficient to control all spectral components with sufficient accuracy, the final penalty function J can include a regularisation term Jb as , where the parameter α can be tuned (between 0 and 1) to modify the importance of Jb with respect to Jo. The regularisation term Jb is the following norm of the spectral amplitudes flm of Eq. (2):
where σlm is typically the standard deviation of the signal along each spherical harmonics.
In practice, several additional modifications may need to be introduced in the algorithm and have been implemented for our study. (i) For a non-global model domain (such as CREG4), it may be better to reduce the basis of the spherical harmonics (for each degree l) to the subspace that is effectively spanned by the prior ensemble. (ii) For numerical efficiency reasons, it can be useful to perform the regression locally (over a local range of degree l) and then iterate until convergence. (iii) In the case of large regions without observations (such as the Nordic Seas for spatial altimetry), it can be useful to add zero bogus observations to avoid triggering a spurious signal where no observation is available. For instance, in our study, we added observations in the northern region of the domain, where no Jason observations are available.
3.3.2 Observational error
The observational error results from both the initial Gaussian error with a standard deviation of 5 cm introduced on the true member to create the observation and also the partial observation coverage and hence the algorithm used to do the regression. In theory, this error can be quantified. We suppose that the observational error is decorrelated at large scales. Indeed, the large-scale correlations of this observational error are small compared to the observed large-scale structures. This assumption will be verified in Sect. 5.2 by the consistency of the rank histograms. As part of our twin experiment, we propose the following procedure.
This error has been quantified following these steps. In this twin experiment, the true state is known. The chosen true member, from which the observation has been created, initially belongs to an ensemble of members. Then, in the same ways described above, N+1 true members, with can be used to generate observations yo, i. It is then possible to evaluate the standard deviation of the observational error in the spectral domain by transforming (i) the innovation vector and (ii) the misfit with respect to the true state and by computing the rms difference between these two transformed vectors. More explicitly, this is done by computing the rms between , where the operator STregr provides the spectrum resulting from the regression of innovations , and , where the operator ST provides the spectrum of the corresponding true anomalies , following Eq. (2).
This method is directly applicable to twin experiments and can be transposed to a real system by simulating observational error and looking at how it is transformed in the spectral domain. In a realistic case, the above method can directly be transposed by simulating observational error in model results and by transforming the difference between the perturbed and unperturbed data. The standard deviation of the result is then an estimate of the observation error standard deviation along each spherical harmonics.
3.4 Transformed correlation structure
We need to study the main dependencies and correlations between the different spectral components of the ocean fields in order to determine whether and how the scale separation could be used in the data assimilation scheme. Figure 5 shows two examples of ensemble correlation maps between spectral amplitudes. It is comparable to Fig. 2 but in the spectral domain (amplitudes flm of Eq. 2). Ensemble correlation structure is computed according to reference points in the spectral domain and indicated by crosses in Fig. 5. It shows how the assimilation of the signal of an observation at these reference points will impact the other scales during the spectral analysis step. Similarly to Fig. 2, the significant and maximum area is confined near the reference points. Most correlations between very different scales are weak and might thus be neglected by data assimilation. This is the basic property allowing to introduce scale separation in the data assimilation scheme with a reasonable cost. However, it is true that there are also significant correlations for remote scales, and that neglecting these correlations corresponds to losing potentially useful information. This is however similar to what happens with spatial localisation: in Fig. 2, there also exists significant correlations far from the reference location. The question is then which correlations is it better to neglect to preserve the meaningful structures contained in the ensemble. This is the question that we will try to elucidate with our example application.
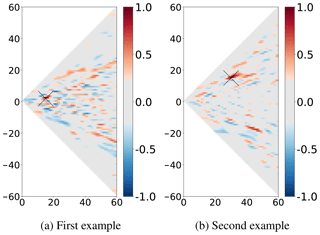
Figure 5Two examples of ensemble correlation for the prior ensemble (SSH) in the spectral domain, according to the degrees in the abscissa and m in the ordinate; see Eq. (2). The two different reference points are indicated by black crosses. Light grey colour corresponds to non-significant values of ensemble correlations for an ensemble of N=69 members (smaller in absolute value than 0.2367 with significance threshold at 95 %).
To exploit this property of weak correlations between very different scales, a spectral analysis thus also requires to be localised, at least for the large scales in our study. The method of spectral localisation is the same as that usually used in the spatial domain. For the same reasons, each localisation window will contain a number of degrees of freedom sufficiently low to be controlled with an ensemble of moderate size.
The objective of this section is to introduce and demonstrate the multiscale observational update algorithm, combining spectral localisation for the large scales and spatial localisation for the small scales. In Sect. 4.1, we show how spectral localisation can be obtained using the spectral transformation presented in Sect. 3 and how it can be combined with spatial localisation to build up the multiscale observational update algorithm. In Sect. 4.2, we compare the spatial and spectral localisation schemes and demonstrate the improvement brought by spectral localisation in the control of the large scales. In Sect. 4.3, we use this comparison to determine the critical scale, lc, above which spatial localisation starts performing better than spectral localisation. This critical scale is the key parameter that specifies how spatial and spectral localisation are combined in the multiscale observational update algorithm.
4.1 Multiscale observational update algorithm
We propose an algorithm for the multiscale analysis based on a combination of a spectral analysis with spectral localisation for the large scales (described by Eq. 7) and a spatial analysis with spatial localisation for the residual scales (described by Eq. 6). The large scales are defined by the critical scale lc. The full algorithm is explained by Eqs. (8) to (12). For this new method, we need to combine an algorithm to perform the observational update (OU) of the ensemble with the forward (ST) and backward (ST−1) spectral transformations previously defined by Eqs. (2) and (3). Any observational update algorithm can be chosen provided that it allows localisation, for instance, the SEEK observational update (Brasseur and Verron, 2006) or the ETKF observational update (Bishop et al., 2001). This localisation will be applied in our case in the spectral domain (OUspectral) or in the spatial domain (OUspatial) depending on the context.
4.1.1 Spatial and spectral localisation
The analysis step is usually done in the spatial domain with a spatial localisation (observational update OUspatial) using spatial innovation. This step is applied to the prior ensemble anomaly, , with respect to prior ensemble mean (for member ) to obtain the updated ensemble . It corresponds to the correction applied to the prior ensemble during the assimilation step.
Another approach is to apply the observational update in the spectral domain with spectral localisation (OUspectral) to the prior ensemble () after transformation into the spectral domain (ST). The spectral innovation is computed following Sect. 3.3.1. The resulting spectral analysis ( with superscript LS for large scales) is only available up to the scale lc, for which the spectral transformation has been done.
4.1.2 Multiscale analysis: description of the algorithm
Multiscale analysis combines a spectral localisation for the large scales and spatial localisation for the residual scales.
-
First step: spectral localisation for the large scales. This is an observational update with spectral localisation for the large-scale part of the ensemble anomalies, as already described in the previous section; see Eq. (7).
-
Second step: spatial localisation for the residual part. Extract : the residual part of each anomaly of the prior ensemble:
Then, compute δyRes: the residual part of the innovation, using the current best estimate of the large-scale field at the observation points:
Compute : the residual part of the ensemble analysis increment, using the residual spatial innovation (δyRes) during the observational update in the spatial domain with spatial localisation (OUspatial). Spatial observational error has to be estimated and can be smaller than those chosen for the spatial localisation only (see Eq. 6) to get better results at each scale. Indeed, a part of the error has already been taken into account during the spectral localisation for the large scales.
-
Third step: full spectrum. Compute : the final value of the ensemble analysis for the member i as the sum of Eqs. (8) and (11):
This analysis increment is directly comparable to the analysis increment obtained with the spatial localisation applied to the full field; see Eq. (6).
4.2 Comparison of localisation schemes
The relevance of implementing a multiscale analysis rather than the usual spatial localisation is only validated if spectral localisation better retrieves large-scale patterns of the signal than spatial localisation. To verify the validity of this assumption, we perform two different analyses in the context of the twin experiments described in Sect. 2.2. The first analysis is carried out with a spatial localisation only following Eq. (6), hereinafter called spatial localisation, whereas the second analysis uses a spectral localisation only following Eq. (7), hereinafter called spectral localisation. Spatial and spectral localisation radius have been optimised to obtain the best results in both experiments. The spatial localisation radius corresponds to a wavelength of spherical harmonic about 139 km at the Equator, while that of spectral localisation is a rectangle of 3 in ordinate l number and 1 in m number. They have been deduced from the correlation ensemble (see, for instance, Fig. 2a and b for spatial localisation, and Fig. 5a and b for spectral localisation). The localisation radius is chosen small enough to avoid non-significant correlations. In order to evaluate these localisation algorithms, they are compared for the large scales. As justified later in Sect. 4.3, we choose to define large scales as the range of scales .
Each scale of spatial and spectral analysis increments has to be as close as possible to the corresponding scale of the true anomaly. The large-scale part of this spatial analysis increment ( of Eq. 6) can be directly compared to the spectral analysis increment obtained from the large scale of the prior ensemble ( of Eq. 7). It can be extracted, following Eqs. (2) and (3), to obtain the corresponding large scales of the spatial analysis increment:
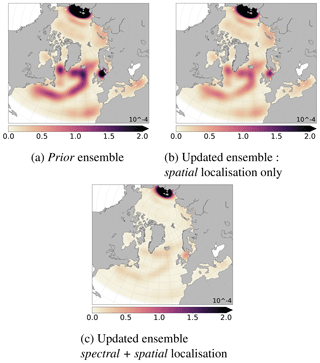
Simultaneously, the obtained spectral analysis increment (Eq. 7) is back into the spatial domain (applying ST−1, following Eq. 3) to be directly comparable to the large scales of the spatial analysis increment (Eq. 13). Figure 6a and b show, respectively, the large scale of the mean ensemble of analysis increments obtained, respectively, with spatial localisation or spectral localisation (see Sect. 4.1.1). Hence, they have to be as similar as possible to the large-scale part of the true anomaly shown in Fig. 4c.
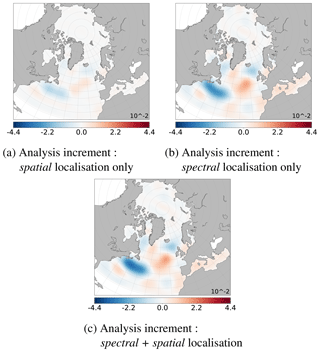
Figure 6Ensemble mean of large-scale part of the analysis increments (SSH in metres), with , lc=34: (a) obtained after spatial localisation only and then filtered; see Eqs. (6) and (3); (b) obtained after spectral localisation following Eq. (7); (c) obtained after multiscale analysis (spectral + spatial localisation; see Sect. 4.1.2) (to be compared to the large-scale true anomaly, Fig. 4c).
Spectral localisation recovers large scales much better than spatial localisation; see Fig. 6 vs. Fig. 4c. In all cases, the analysis increment is significant only where Jason data are available (see Fig. 1d). The analysis and the type of localisation thus have no significant impact on the north of the model domain. This result reinforces the idea of a multiscale analysis with spectral localisation for the large scale. It is now necessary to determine the critical scale, lc, from which the spatial localisation will be preferred.
4.3 Determining the critical scale
On average, spectral localisation only gives better results than spatial localisation for the large scales, but we need to check that this affirmation remains valid at each scale or that there exists a critical scale, lc, from which this tendency is no longer true. To determine lc, a classic score is computed for the spatial localisation and the spectral localisation. It shows the improvement of the RMSE after/before the analysis by averaging sums over the whole model domain:
where is the mean over the domain. Each member of this equation is then computed for all specific degree l, following Eqs. (2) and (3) with . During an analysis step, the RMSE of the observed variable will be reduced. The ratio thus allows to evaluate the accuracy of the analysis for each scale. Figure 7 shows this score for each degree l until 100 for the spatial analysis only and until 60 for the spectral analysis only.
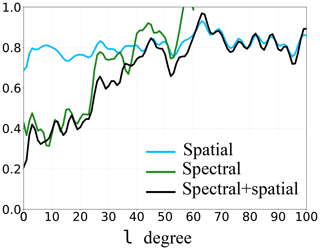
Figure 7Reduction of spatial RMSE for each degree for the SSH, computed using Eq. (14). The blue curve (spatial) refers to the spatially updated ensemble, the green curve (spectral) to the spectrally updated ensemble and the black curve (spectral + spatial) to the multiscale updated ensemble.
This gives a new point of view to evaluate the results of an analysis, giving the efficiency of the spatial or spectral analysis at each scale and no longer only for the full field. Spatial localisation deals with all scales at the same time. The score is almost the same at each scale: around 0.8. In contrast, this score of the spectral localisation is very sensitive to the scale. It is almost up to 2 times smaller than the one of the spatial localisation for the large scales. It increases with the degree until it becomes similar and exceeds the spatial localisation score. The spectral observational error used for the spectral localisation has not been computed exactly from l≈50. This led to important values close to l=60, which impact the score shown in Fig. 7. However, if observational error has been computed exactly until larger degrees, the trend would follow a similar pattern.
Until around l≈34, spectral localisation further reduces the spatial RMSE more than spatial localisation, which is consistent with the study of analysis increments in Fig. 6, while, for larger degrees l, this trend tends to reverse. The critical value, lc, does not need to be very precise for the multiscale analysis. Indeed, the scores of spatial and spectral localisations are close on a range of degrees (here around 30 and 50, for instance). A variation of a few degrees on lc will not have any major impact on the final results of the multiscale analysis. In this twin experiment and for all these reasons, the critical scale lc is now fixed to lc=34.
The aim of this section is to evaluate the multiscale analysis and to compare it with spatial analysis, for the full spectrum but also at each scale. For that purpose, we did a multiscale analysis following the algorithm presented in the previous Sect. 4.1.2, with the critical scale lc=34. This experiment is hereinafter called spectral + spatial localisation in figures.
In Sect. 5.1, we demonstrate that multiscale analysis keeps the advantages of spectral and spatial localisations at each wavelength. This is done by studying the error of spatial RMSE for each scale and comparing the analysis increment for the multiscale analysis and the spatial localisation. In Sect. 5.2, we check the reliability of these updated ensembles by computing rank histograms in the spatial and also spectral domains. In Sect. 5.3, we show that the spread of the updated ensembles obtained with the multiscale analysis decreases much more than those of the spatial localisation at large scales, as well as for all scales. In Sect. 5.4, we evaluate the impact of the multiscale analysis on the non-observed variables (temperature and salinity) with a multivariate analysis. We show that on average multiscale analysis reduces their spatial RMSE much more than the spatial localisation for large scales and similar errors at smaller scales.
5.1 Error reduction at each wavelength
On average, the updated ensemble produced with the multiscale analysis should better approach the true state than those obtained with the spatial localisation only. To evaluate the efficiency of the multiscale analysis, the error has been computed in two ways: at each scale in the spectral domain, following Eq. (14), and in the spatial domain for the full spectrum, with a comparison of the analysis increments and the true state.
5.1.1 Spectral point of view: reduction of spatial RMSE for each scale
The previous score showing the evolution of the RMSE after/before the analysis on average on the model domain, following Eq. (14), is now computed for the multiscale analysis. Figure 7 (black curve) shows this score computed for each scale until l=100.
Multiscale analysis keeps the advantages of both localisations (spectral localisation in green and spatial localisation in blue). As expected, for the large scales , with lc=34, the multiscale analysis is much better than spatial localisation and has the same order of magnitude as the spectral localisation. Indeed, the same spectral localisation with the same configuration has been done for the multiscale analysis. For the residual scales, multiscale analysis allows to recover, as expected, similar results to the spatial localisation, especially for the smaller scales. Differences occur especially close to lc and result from the contribution of the spatial localisation to treat the residual scales. To explain why small difference exists between the black and the green curves before the critical scale, we have to note that the analysis increment obtained with the spatial localisation can include a large-scale component, which can directly impact the large scale of the total analysis increment.
5.1.2 Spatial global point of view: analysis increment
The analysis increments obtained with spatial localisation (Fig. 8a) or with multiscale analysis (spectral + spatial localisation; Fig. 8b) can be directly compared to the full spectrum of the true anomaly shown in Fig. 1c. The multiscale analysis allows to recover a part of the large-scale pattern unlike the spatial localisation. It keeps advantages of the spatial localisation for the residual scales.
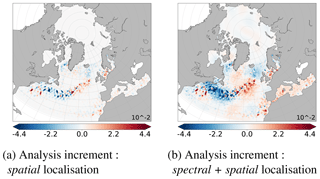
These analysis increments can be evaluated at each scale. Figures 6a and c show the large scales () of these analysis increments, respectively, for spatial localisation or multiscale analysis. They have been obtained from their respective full fields (Fig. 8a and b) following Eqs. (2) and (3). Small structures have been well removed from the full spectrum. They have to be as close as possible to the large scales of the true anomaly shown Fig. 4c, which have been extracted from its full field shown in Fig. 1c. Multiscale analysis and spectral localisation give similar results for the large scales and are better than the spatial localisation. This is consistent with observed reduction of spatial RMSE at each large scale, shown in Fig. 7.
5.2 Reliability of the updated ensemble
The updated ensemble should be reliable in the spatial domain but also in the spectral domain. This involves checking the coherence between the assumed probabilities and the observed statistics when the ensemble is compared to the verification data (the true state in our twin experiment, or observation in a real system). To check ensemble reliability, ranks are traditionally computed in the spatial domain and summarised in a rank histogram. They show the distribution of observations with respect to the ensemble (Anderson, 1996; Talagrand et al., 1997). In our context of twin experiments, the prior ensemble is reliable by construction. Indeed, the true state originates from the same ensemble simulation as the other members. The reliability of the updated ensemble will be evaluated by comparing the rank histogram of the updated ensemble with the rank histogram of the prior ensemble. Hence, a flat rank histogram indicates a reliable ensemble, whereas a U-shaped rank histogram indicates a lack of spread in the ensemble: the uncertainty is underestimated (Anderson, 1996; Hamill, 2001). Alternatively, we propose a new point of view of these ranks, computing them in the spectral domain. The interpretation of these new ranks has to corroborate the conclusions obtained in the spatial domain.
5.2.1 Spatial rank histograms
Rank histograms have been computed, with respect to the true state, from spatial maps limited to the Jason domain for the prior ensemble, the spatially updated ensemble and the multiscale updated ensemble. Figure 9b shows the rank histograms for the large scales () for the same ensembles but also for the spectrally updated ensemble presented in the previous section.
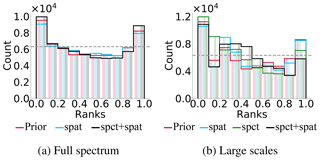
Figure 9Spatial rank histogram on the Jason domain for the SSH. “Prior” (in red), “spat” (in blue), “spct” (in green) and “spct + spat” (in black) correspond, respectively, to the prior ensemble, spatially updated ensemble, spectrally updated ensemble and the multiscale updated ensemble. (a) Full spectrum; (b) after extraction of the large scales: , with lc=34.
Rank histograms show that all these updated ensembles can be considered as reliable as the prior ensemble, both for the full spectrum and for the large scales. Indeed, the prior ensemble looks somewhat underdispersed but can be considered reliable because the true member originates from the ensemble itself. The rank histograms of the updated ensembles are of the same order of magnitude as that of the prior ensemble. Thus, the small underdispersion of the prior ensemble (which can only result from the limited size of the sample) has not increased during the analysis step. These consistent rank histograms confirm that the observational error has been properly evaluated.
5.2.2 A new point of view: ranks map in the spectral domain
Reliability of all updated ensemble (spatial localisation only and multiscale analysis) is now tested for degrees by calculating ranks in the spectral domain with respect to the true state. Ranks are computed following the same procedure as in the spatial domain but the members and the true state are previously transformed into the spectral domain following Eq. (2). Figure 10 shows the maps of ranks in the spectral domain for the prior ensemble, the spatially updated ensemble and the multiscale updated ensemble. The maps of ranks for the spectrally updated ensemble are not shown due to similar results to the multiscale updated ensemble. This new point of view allows to diagnose the behaviour of the system for each scale.
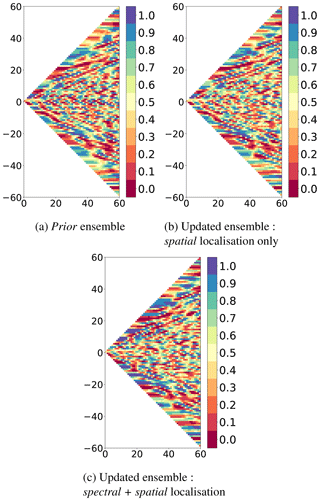
Figure 10Maps of ranks in the spectral domain for the SSH, according to the degrees in the abscissa and m in the ordinate; see Eq. (2). (a) Prior ensemble; (b, c) updated ensembles, respectively, obtained after spatial localisation only (see Eq. 6) or after the multiscale analysis (spectral + spatial localisation; see Sect. 4.1.2).
Ranks maps in the spectral domain provide additional indication that all algorithms provide reliable updated ensembles. Observational error has been consistently evaluated. The ranks are computed for each spectral coordinate (l, m) and have been normalised by the total number of data points to have numbers between 0 and 1. For a perfectly reliable ensemble, ranks would be evenly and randomly distributed over the entire spectral domain. For our study, when degrees tend toward l=m, which corresponds to meridional signal, ranks are not all represented even for the prior ensemble. However, these spectral regions correspond to extremely weak standard deviation of the ensemble in the spectral domain (see Fig. 3a): there is no meridional signal in the prior ensemble. They do not have an important impact on the spatial field. For the other degrees, ranks show that the prior ensemble is reliable. The spatially updated ensemble and the multiscale updated ensemble also remain reliable even if the latter seems to be somewhat less dispersed.
5.3 Resolution of the updated ensemble
The spread, or variance, of the prior and the updated ensemble (with N=69 members) has been computed to check the resolution of the updated ensemble. For instance, for the prior ensemble, xf,
The reliability of the ensemble has been checked previously with the rank histograms. Then, the smaller the spread after the analysis, the better the analysis. Figures 11 and 12 show the spread of the prior ensemble, the updated ensemble after spatial localisation and the updated ensemble after a multiscale analysis (spectral + spatial localisation), respectively, for the full spectrum and after extraction of the large scales (, with lc=34).
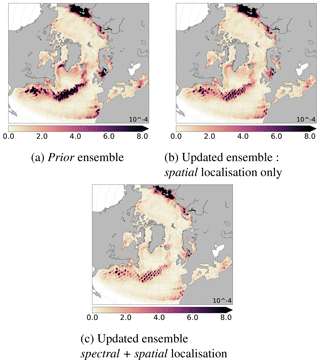
Figure 11Ensemble spread of the prior (a), the updated ensembles obtained with (a) the spatial localisation only or with (c) the multiscale analysis (spectral + spatial localisation), according to Eq. (15) (full spectrum) for the SSH.
The multiscale analysis allows to decrease the ensemble spread more than the spatial localisation. The spread is much more reduced along Jason tracks; see Fig. 11c. This decrease is especially important for the large scales; see Fig. 12c. For the large scales, the spread of the updated ensemble by spectral localisation is not shown due to similar results to those of multiscale analysis. Thus, knowing that all these ensembles are reliable, the more efficient algorithm is the multiscale analysis because it has further reduced the spread of the ensemble and is the closest to the true state.
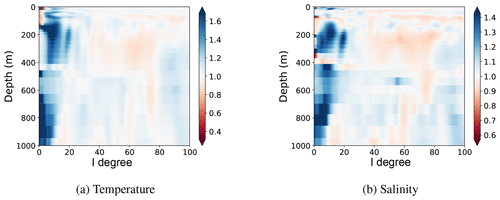
Figure 13Improvement obtained by the multiscale analysis for temperature (a) and salinity (b). This improvement is measured by comparison to spatial localisation only using the ratio in Eq. (16). Blue (respectively red) colour corresponds to a better (respectively worse) correction of the error using the multiscale analysis as compared to spatial localisation only.
5.4 Multivariate analysis
Multivariate analysis consists in extending the observational update to non-observed variables, like temperature and salinity, in the state vector during the analysis. The experimental setup remains the same. The aim is to evaluate the impact of the multiscale analysis on these non-observed variables and to check that it does not introduce more error than the spatial localisation. These errors could increase during the next forecast and cause some unrealistic values. For this purpose, we compute the score defined by Eq. (14) for each degree for the spatial localisation (spat) and for the multiscale analysis (spct+spat). Then, we compute, for each level and each degree, the ratio of these scores, following Eq. (16).
Figure 13 shows these results for the temperature and salinity. Each depth in this figure thus corresponds to the ratio of the blue and black curves of Fig. 7, no longer for the SSH but for the temperature or salinity instead of SSH.
On average, below and around the critical degree lc=34, the multiscale analysis further reduces the error as compared to the spatial localisation only. In a few cases, at basin scales, multiscale analysis appears to produce poorer results than spatial localisation. However, this effect is small as compared to the improvement made at the other depths and large scales. For smaller scales, these two analyses give similar results. It is consistent with the fact that a similar spatial localisation is done for the both analyses and with the results obtained for SSH (see Fig. 7).
We have formulated and evaluated a multiscale analysis approach for ensemble ocean data assimilation that provides a better recovering of the large scales than the current spatial analysis with spatial localisation. It has been developed to be used in the existing data assimilation system of Mercator Océan used in the CMEMS project. This new scheme consists in performing a spectral analysis with spectral localisation for the large scales and a spatial analysis with spatial localisation for the residual scales.
The transformation to the spectral domain and the spectral localisation provides consistent ensemble estimates of the state of the system (in the spectral domain, or after backward transformation to the spatial domain). In terms of accuracy, this spectral localisation recovers the large-scale structures better than the spatial localisation. For the large scales, spectral localisation yields lower errors than spatial localisation while keeping a reliable ensemble. Conversely, the spatial localisation is still preferable for the small scales.
This new spectral approach also gives a new point of view to diagnose the system. Traditional diagnostics as ensemble mean, spread, correlations structures, rank histograms, etc., give information at each scale and no longer only for the full field.
The multiscale analysis, which is a hybrid scheme combining spectral localisation for the large scales and spatial localisation for the residual scales, keeps the advantages of these two localisations. Consequently, it can significantly improve the current use of various ocean observing systems, particularly with regard to the large-scale information contained in sparse distribution of observations as altimeters or ARGO floats.
The direct perspective of this study is to implement and test the method in the real CMEMS system developed at Mercator Océan. The target is (i) to check that the method can be applied without deep modification of the existing system, (ii) to evaluate the operational gain that is obtained by an improved control of the large-scale signal and (iii) to enhance the diagnostic of the system by evaluating the performance separately for each scale. Some data assimilation steps have already been successfully carried out in the same context of our study (not shown). In the longer perspective, the implementation of this multiscale approach for ensembles might improve the CMEMS products of Mercator Océan as the reanalysis which is used by a large scientific community.
The basic code developed to introduce scale separation into the assimilation system is available on request from the authors.
The authors declare that they have no conflict of interest.
This article is part of the special issue “The Copernicus Marine Environment Monitoring Service (CMEMS): scientific advances”. It is not associated with a conference.
This work was conducted as a contribution to the GLO-HR-ASSIM project, funded by the Copernicus Marine Environment Monitoring Service (CMEMS). CMEMS is implemented by Mercator Océan International in the framework of a delegation agreement with the European Union. Additional support for this study was also provided by the CNES/OSTST/MOMOMS project. The calculations were performed using HPC resources from GENCI-IDRIS (grant 2017-011279).
This paper was edited by Marina Tonani and reviewed by Benedicte Lemieux-Dudon and two anonymous referees.
Anderson, J. L.: A Method for Producing and Evaluating Probabilistic Forecasts from Ensemble Model Integrations, J. Climate, 9, 1518–1530, https://doi.org/10.1175/1520-0442(1996)009<1518:AMFPAE>2.0.CO;2, 1996. a, b
Bishop, C. H., Etherton, B. J., and Majumdar, S. J.: Adaptive Sampling with the Ensemble Transform Kalman Filter. Part I: Theoretical Aspects, Mon. Weather Rev., 129, 420–436, https://doi.org/10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2, 2001. a, b
Brankart, J.-M.: Impact of uncertainties in the horizontal density gradient upon low resolution global ocean modelling, Ocean Model., 66, 64–76, https://doi.org/10.1016/j.ocemod.2013.02.004, 2013. a
Brankart, J.-M., Cosme, E., Testut, C.-E., Brasseur, P., and Verron, J.: Efficient Local Error Parameterizations for Square Root or Ensemble Kalman Filters: Application to a Basin-Scale Ocean Turbulent Flow, Mon. Weather Rev., 139, 474–493, https://doi.org/10.1175/2010MWR3310.1, 2011. a, b
Brankart, J.-M., Candille, G., Garnier, F., Calone, C., Melet, A., Bouttier, P.-A., Brasseur, P., and Verron, J.: A generic approach to explicit simulation of uncertainty in the NEMO ocean model, Geosci. Model Dev., 8, 1285–1297, https://doi.org/10.5194/gmd-8-1285-2015, 2015. a
Brasseur, P. and Verron, J.: The SEEK filter method for data assimilation in oceanography: a synthesis, Ocean Dynam., 56, 650–661, https://doi.org/10.1007/s10236-006-0080-3, 2006. a, b
Buehner, M.: Evaluation of a Spatial/Spectral Covariance Localization Approach for Atmospheric Data Assimilation, Mon. Weather Rev., 140, 617–636, https://doi.org/10.1175/MWR-D-10-05052.1, 2012. a
Buehner, M. and Charron, M.: Spectral and spatial localization of background-error correlations for data assimilation, Q. J. Roy. Meteor. Soc., 133, 615–630, https://doi.org/10.1002/qj.50, 2007. a
Buehner, M. and Shlyaeva, A.: Scale-dependent background-error covariance localisation, Tellus A, 67, 28027, https://doi.org/10.3402/tellusa.v67.28027, 2015. a
Caron, J.-F. and Buehner, M.: Scale-Dependent Background Error Covariance Localization: Evaluation in a Global Deterministic Weather Forecasting System, Mon. Weather Rev., 146, 1367–1381, https://doi.org/10.1175/MWR-D-17-0369.1, 2018. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J., Park, B., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Dupont, F., Higginson, S., Bourdallé-Badie, R., Lu, Y., Roy, F., Smith, G. C., Lemieux, J.-F., Garric, G., and Davidson, F.: A high-resolution ocean and sea-ice modelling system for the Arctic and North Atlantic oceans, Geosci. Model Dev., 8, 1577–1594, https://doi.org/10.5194/gmd-8-1577-2015, 2015. a, b
Hamill, T. M.: Interpretation of Rank Histograms for Verifying Ensemble Forecasts, Mon. Weather Rev., 129, 550–560, https://doi.org/10.1175/1520-0493(2001)129<0550:IORHFV>2.0.CO;2, 2001. a
Hamill, T. M., Whitaker, J. S., and Snyder, C.: Distance-Dependent Filtering of Background Error Covariance Estimates in an Ensemble Kalman Filter, Mon. Weather Rev., 129, 2776–2790, https://doi.org/10.1175/1520-0493(2001)129<2776:DDFOBE>2.0.CO;2, 2001. a, b
Houtekamer, P. L. and Mitchell, H. L.: Data Assimilation Using an Ensemble Kalman Filter Technique, Mon. Weather Rev., 126, 796–811, https://doi.org/10.1175/1520-0493(1998)126<0796:DAUAEK>2.0.CO;2, 1998. a, b
Large, W. G. and Yeager, S. G.: The global climatology of an interannually varying air-sea flux data set, Clim. Dynam., 33, 341–364, https://doi.org/10.1007/s00382-008-0441-3, 2009. a
Li, Z., McWilliams, J. C., Ide, K., and Farrara, J. D.: A Multiscale Variational Data Assimilation Scheme: Formulation and Illustration, Mon. Weather Rev., 143, 3804–3822, https://doi.org/10.1175/MWR-D-14-00384.1, 2015. a
Madec, G.: NEMO ocean engine, Note du Pôle de modélisation, Institut Pierre-Simon Laplace (IPSL), France, No 27, ISSN 1288-1619, 2008. a, b
Miyoshi, T. and Kondo, K.: A Multi-Scale Localization Approach to an Ensemble Kalman filter, SOLA, 9, 170–173, https://doi.org/10.2151/sola.2013-038, 2013. a
Pham, D. T., Verron, J., and Roubaud, M.-C.: A singular evolutive extended Kalman filter for data assimilation in oceanography, J. Marine Syst., 16, 323–340, https://doi.org/10.1016/S0924-7963(97)00109-7, 1998. a
Talagrand, O., Vautard, R., and Strauss, B.: Evaluation of probabilistic prediction systems, in: Workshop on Predictability, 20–22 October 1997, 1–26, ECMWF, Shinfield Park, Reading, 1997. a
Testut, C.-E., Brasseur, P., Brankart, J.-M., and Verron, J.: Assimilation of sea-surface temperature and altimetric observations during 1992–1993 into an eddy permitting primitive equation model of the North Atlantic Ocean, J. Marine Syst., 40–41, 291–316, https://doi.org/10.1016/S0924-7963(03)00022-8, 2003. a, b
Wunsch, C. and Stammer, D.: The global frequency-wavenumber spectrum of oceanic variability estimated from TOPEX/POSEIDON altimetric measurements, J. Geophys. Res., 100, 24895, https://doi.org/10.1029/95JC01783, 1995. a
Zhang, F., Weng, Y., Sippel, J. A., Meng, Z., and Bishop, C. H.: Cloud-Resolving Hurricane Initialization and Prediction through Assimilation of Doppler Radar Observations with an Ensemble Kalman Filter, Mon. Weather Rev., 137, 2105–2125, https://doi.org/10.1175/2009MWR2645.1, 2009. a
Zhou, Y., McLaughlin, D., Entekhabi, D., and Ng, G.-H. C.: An Ensemble Multiscale Filter for Large Nonlinear Data Assimilation Problems, Mon. Weather Rev., 136, 678–698, https://doi.org/10.1175/2007MWR2064.1, 2008. a