the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Frontogenesis of the Angola–Benguela Frontal Zone
Hervé Giordani
Katerina Goubanova
A diagnostic analysis of the climatological annual mean and seasonal cycle of the Angola–Benguela Frontal Zone (ABFZ) is performed by applying an ocean frontogenetic function (OFGF) to the ocean mixing layer (OML). The OFGF reveals that the meridional confluence and vertical tilting terms are the most dominant contributors to the frontogenesis of the ABFZ. The ABFZ shows a well-pronounced semiannual cycle with two maximum (minimum) peaks in April–May and November–December (February–March and July–August). The development of the two maxima of frontogenesis is due to two different physical processes: enhanced tilting from March to April and meridional confluence from September to October. The strong meridional confluence in September to October is closely related to the seasonal southward intrusion of tropical warm water to the ABFZ that seems to be associated with the development of the Angola Dome northwest of the ABFZ. The strong tilting effect from March to April is attributed to the meridional gradient of vertical velocities, whose effect is amplified in this period due to increasing stratification and shallow OML depth. The proposed OFGF can be viewed as a tool to diagnose the performance of coupled general circulation models (CGCMs) that generally fail at realistically simulating the position of the ABFZ, which leading to huge warm biases in the southeastern Atlantic.
- Article
(4918 KB) -
Supplement
(413 KB) - BibTeX
- EndNote
The Angola-Benguela Frontal Zone (ABFZ, see Fig. 1), situated off the coast of Angola and Namibia, is a key oceanic feature in the southeastern Atlantic Ocean. The ABFZ separates the warm sea water of the Angola Current (e.g., Kopte et al., 2017) from the cold sea water associated with the Benguela Current and upwelling system (e.g., Mohrholz et al., 2004; Colberg and Reason, 2006, 2007; Veitch et al., 2006; Fennel et al., 2012; Chen et al., 2012; Santos et al., 2012; Goubanova et al., 2013; Junker et al., 2015, 2017; Vizy et al., 2018). The ABFZ is characterized by a smaller spatial extent and weaker sea surface temperature (SST) gradient compared to the major oceanic fronts generated by the western boundary currents (Fig. 1). However, due to its near-coastal location, the ABFZ plays important roles for the southern African continent, strongly impacting the local marine ecosystem (e.g., Auel and Verheye, 2007; Chavez and Messié, 2009) and regional climate (Hirst and Hastenrath, 1983; Rouault et al., 2003; Hansingo and Reason, 2009; Manhique et al., 2015). In particular, the main mode of interannual variability in SST in the ABFZ, the so-called Benguela Niño/Niña (e.g., Florenchie et al., 2003; Rouault et al., 2018), influences the local rainfall along the southwestern African coast of Angola and Namibia via moisture flux anomalies associated with the SST anomalies (Rouault et al., 2003; Hanshingo and Reason, 2009; Lutz et al., 2015) and tends to have a remote impact on rainfall activity over the southeastern African continent (e.g., Manhique et al., 2015).
The ABFZ region also poses one of the major challenges for the global climate modeling community. Most CGCMs exhibit a huge warm SST bias in the ABFZ (e.g., Zuidema et al., 2016) and fail to reproduce the realistic SST, its seasonal cycle, and the right location of the ABFZ (e.g., Koseki et al., 2017). While Colberg and Reason (2006) and Giordani and Caniaux (2011) concluded that the position of the ABFZ is controlled, to a large extent, by the local wind stress curl, Koseki et al. (2018) elucidated that the local wind stress curl bias in CGCMs contributes partly to the warm SST bias in the ABFZ via erroneous intrusion of tropical warm water, which is induced by a negative wind stress curl and enhanced Angola Current. In order to comprehensively understand the sources of such model biases, one needs to understand the processes of generation of the ABFZ.
Previous studies have mainly focused on the SST variability at interannual to decadal timescales in the ABFZ, and/or on its impacts on regional climate that are well-studied (e.g., Rouault et al., 2003; Lutz et al., 2015; Vizy et al., 2018). Whereas Morholz et al. (1999) analyzed the ABFZ during a particular event in 1999, to our knowledge there are few or no works quantitatively investigating dynamical and thermodynamical processes responsible for the climatological state of the ABFZ and its seasonal cycle. A dynamical diagnosis for the SST front in the north of the Atlantic cold tongue (e.g., Hasternrath and Lamb, 1978; Giordani et al., 2013) was proposed by Giordani and Caniaux (2014, hereafter referred to as GC2014). The frontogenetic function they use is, in general, adapted to explore sources of frontogenesis of atmospheric synoptic-scale cyclones in the extratropics (e.g., Keyser et al., 1988; Giordani and Caniaux, 2001). Using a frontogenetic function, GC2014 clearly showed that the convergence associated with the northern South Equatorial Current and Guinea Current forces the SST-front intensity (frontogenetic effect), whereas mixed-layer turbulent flux destroys the SST front (frontolytic effect). Fundamentally, the frontogenetic function consists of three mechanical terms (confluence, shear, and tilting) and two thermodynamical terms (diabatic heating and vertical mixing). Around the ABFZ, all these terms can be considered to be contributors to the frontogenesis due to (1) the confluence zone associated with the southward Angola and northward Benguela currents (confluence and shear), (2) strong coastal upwelling (tilting) associated with the Benguela Current, (3) spatial variations in radiative fluxes induced by the stratocumulus cloud deck (diabatic heating related to radiation) associated with the cold SST and subsidence due to the St. Helena anticyclone (e.g., Klein and Hartmann, 1993; Pfeifroth et al., 2012). So far, the relative roles of these different processes in the frontogenesis of the ABFZ still need to be investigated.
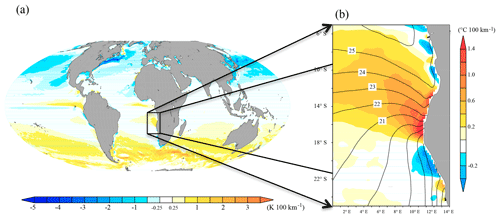
Figure 1(a) Global image of observed 1982–2010 OISST. (b) Annual-mean SST (contour, ∘C) and its meridional gradient (∘C per 100 km) around the ABFZ.
In this study, following the fundamental philosophy of GC2014, we attempt to understand the mechanisms responsible for the climatological ABFZ development at a seasonal timescale based on a first-order estimation. We propose an ocean frontogenetic function (OFGF) in a different way from GC2014 focusing on the OML mean front. The structure of the remainder of this paper is as follows. Sect. 2 gives details of dataset used in this study. In Sect. 3, we derive the OFGF. Section 4 provides a description of the climatological state around the ABFZ. In Sect. 5, we apply our diagnostic methodology to the ABFZ and determine the main terms of the frontogenetic function controlling its annual mean and seasonal cycle. The associated processes are discussed in Sect. 6. Finally we summarize and make some concluding remarks in Sect. 7.
For an overview of SST and its meridional gradient in the ABFZ, and evaluation of the reanalysis data, we employ the optimum interpolated sea surface temperature (OISST; Reynolds et al., 2007) released by the National Oceanic and Atmospheric Administration (NOAA) that has 0.25∘of horizontal resolution and daily temporal resolution from 1982 to 2010. For the 3-D diagnostic analysis of the ABFZ, we utilize 1 h forecast data of the Climate Forecast System Reanalysis (CFSR; Saha et al., 2010) developed by the National Centers for Environmental Prediction (NCEP). The ocean component of this system is based on Modular Ocean Model (MOM) version 4p0d (Griffies et al., 2004) and implements data assimilation for the forecast. This system provides 6-hourly data with a 0.5∘ horizontal resolution and 70 vertical layers for ocean. This resolution is relatively coarse compared to the resolution of simulations performed with regional ocean models in a forced mode using wind forcing from satellite products. However, the advantage of a coupled ocean–atmosphere system like CFSR is that it allows for avoiding spurious effects in wind forcing over coastal regions resulting from the extrapolation in a 25–50 km width coastal fringe where the wind cannot be observed by scatterometers (Astudillo et al., 2017). Moreover, the wind satellite products are generally available for only a relatively short time period, limiting investigation of long-term climatology and seasonal cycle. In this paper we will analyze daily means (the procedure of data post-processing is given in the Supplement) and utilize the CFSR outputs of velocity (horizontal and vertical), potential temperature, net surface heat flux, OML depth, and sea surface height (SSH).
The OFGF is defined and applied to the OML in order to propose a dynamical diagnosis of the maintenance and generating process of the ABFZ. Following GC2014, we use the OFGF as a tool to unravel the Lagrangian (pure) sources of the oceanic front. While there is plenty of literature investigating the ocean-front dynamics (e.g., Dinniman and Rienecker, 1999), the concept of this OFGF has been hardly referred to. The Lagrangian frontogenesis function, F, is defined as
where θ is the temperature. While the frontogenetic function is generally defined as the square of the horizontal gradient of the temperature (e.g., GC2014), our study only employs the meridional gradient of the temperature because the ABFZ SST-gradient is oriented south–north. The right-hand side of Eq. (1) can be written as,
and using
we obtain
Here, u, v, and w denote the zonal, meridional, and vertical current velocities, respectively. Equation (2) describes the processes that act to generate or destroy the ocean front. The terms , , and are the contributions due to the mechanical processes: shear, convergence, and tilting, respectively. The shear term represents conversion of the zonal temperature gradient into meridional gradient by zonal current shear. In particular, the cool SST associated with the Benguela upwelling creates a strong zonal gradient in the south of the ABFZ (e.g., Morholz et al., 1999). The shear term can explain the conversion of such a zonal gradient into meridional gradient. The convergence term represents strengthening or weakening of the meridional temperature gradient by convergence or divergence of meridional current. The tilting term represents conversion of the vertical stratification into meridional gradient by meridional shear of vertical velocity.
The fourth term is a thermodynamical term due to exchange of heat associated with the turbulent heat flux (surface heat flux is included into ; it is the surface boundary condition). The contribution due to the second-order horizontal diffusion is ignored for simplicity.
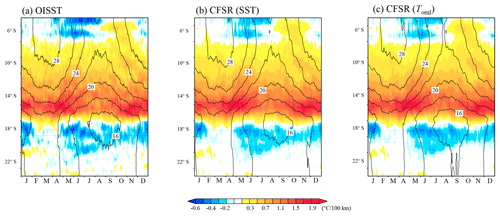
Figure 2Climatological seasonal cycle of the temperature (contour) and its meridional gradient averaged between 10 and 12∘ E for (a) SST of OISST, (b) SST of CFSR, and (c) OML-mean potential temperature of CFSR.
Since within the OML the temperature is fairly uniform (cf. Fig. 2 to compare the SST and OML-averaged temperature), we consider the OFGF with the mixed-layer mean quantities. With the approximation that temperature is independent of the depth in the OML (e.g., Kazmin and Rienecker, 1996; Tozuka and Cronin, 2014), Eq. (2) can be expressed as
where the subscript oml indicates the OML-mean quantity estimated by
where D denotes the OML depth, i.e., the terms with subscript oml include the changes in the OML implicitly. Although the horizontal velocity is a function of depth even in the OML, the horizontal mechanical terms in Eq. (3) can be written in terms of OML-mean quantities because the production is linear in u and v as long as the temperature is independent of depth in the OML. Symbols wb, we, Δθ, and D represent the vertical velocity, the entrainment velocity, the temperature jump at the bottom of the OML, and the OML depth, respectively. According to Moisan and Niller (1998), the entrainment velocity at the bottom of the OML is estimated by
where ub is the horizontal velocity at the bottom of the OML. Δθ is estimated as the difference between the OML-mean temperature and the temperature just below the OML. We use constant values for sea water density, ρ (1000 kg m−3), and isobaric specific heat of sea water, Cp (4200 J kg−1 K−1). The vertical mixing term is replaced with Qs and Qb, where is the surface net heat flux at the top of the OML (downward is positive in this study) and represents the vertical mixing at the bottom of the OML, i.e., in the thermocline. We assume that there is no penetration of shortwave radiation beyond the OML to deeper ocean layers. Because the vertical turbulent mixing term at the mixed-layer base Qb is represented according to K-profile parameterization in ocean–atmosphere general circulation models (OAGCMs), it will not be explicitly addressed in this study as it is not possible to estimate it from the reanalysis outputs.
While Eq. (3) is the Lagrangian form of the OFGF, the equation can also be expressed in Eulerian form as below:
In this equation, the kinematic and diabatic Qb entrainment terms, and the horizontal and vertical advection terms of , are included in the residual (RESD). Accurate estimation of the entrainment terms are not possible from CFSR outputs and the horizontal and vertical advection effects are not related to Lagrangian sources of the frontogenesis. In the remainder of this paper, the shear term will be referred to as SHER, the confluence as CONF, the tilting as TILT, the thermodynamic term as SFLX, and the residual as RESD.
Note that our climatology is a 29-year mean from 1982 to 2010 (the procedure of making daily climatology of temperature meridional gradient and OFGF are described in the Supplement). However, some years do not have OML data at some grid points around the coastal region. For these grid points, we make the climatology only for available years. For example, the smallest number in the focusing ABFZ is 16 years at 16.25∘ S.
Before the dynamical diagnosis is performed, we provide a brief overview of the main features of the ABFZ. The maximum of the ABFZ (up to 1.4 ∘C per 100 km) is located at 16∘ S just near the coast (Fig. 1b). Figure 2a shows a seasonal cycle of the temperature and its meridional gradient obtained from the satellite product OISST. In this study, the maximum value of the meridional SST gradient is defined as the intensity of the ABFZ. The core (SST meridional gradient exceeds 1.0 ∘C per 100 km) of the ABFZ always lies between 17 and 15∘ S. At the climatological seasonal timescale, the location of the ABFZ exhibits a rather weak variability compared to strong interannual variability associated with the Benguela Niño events that push the ABFZ southward due to the southward intrusion of tropical warm water (e.g., Gammelsrød et al., 1998; Veitch et al., 2006; Rouault et al., 2017). For instance, Rouault et al. (2017) showed that during the Benguela Niño 2010–2011 the ABFZ displaced southward as far as 20∘ S. The intensity of the ABFZ shows a pronounced seasonal cycle: there are two peaks in the strength in April to May and November to December, respectively. The semiannual cycle of the ABFZ will be examined in more detail in the following sections. Figure 2b and c evidence that the CFSR reanalysis reproduces realistically the annual cycle of the ABFZ, and that the annual cycle of the corresponding OML-mean temperature meridional gradient is representative of the annual cycle of the SST meridional gradient in terms of both timing and intensity of the two annual peaks. This latter result justifies our approach to diagnose the frontogenesis of the ABFZ with the OML-mean quantities.
In this section, we investigate the frontogenesis of the ABFZ by diagnostically applying the OFGF described in Sect. 3. Figure 3 illustrates the climatological annual-mean oceanic dynamical fields. The southwestward Angola and northwestward Benguela alongshore currents collide just south of the ABFZ. Seaward from the ABFZ, a strong westward current is detected. An intense upwelling (vertical velocity at the bottom of OML exceeding 0.18 m day−1) is generated along the coast in the Benguela Current region. A local maximum of upwelling in the ABFZ (approximately 17∘ S) corresponds to one of the most vigorous upwelling cells in the region, namely the Kunene upwelling cell (Kay et al., 2018). Note also a relatively weak downwelling cell (vertical velocity down to −0.06 m day−1) just seaward from the Kunene upwelling cell.
5.1 Annual-mean state
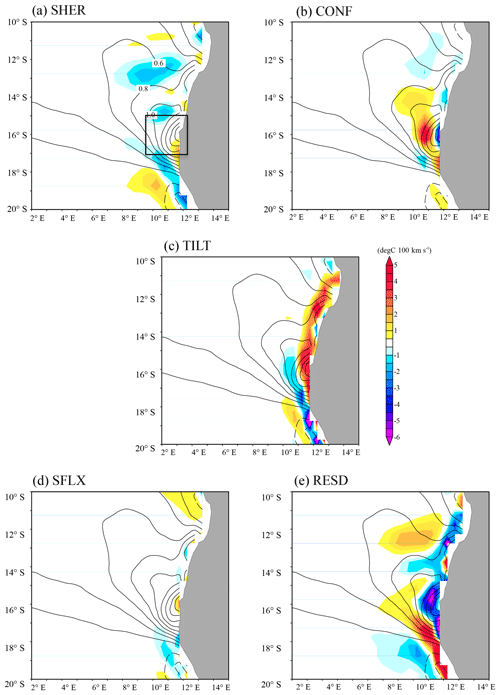
Figure 4 presents the annual-mean climatology of the 5 forcing or source terms of the OFGF superimposing the meridional gradient of the OML-mean temperature. SHER works frontolytically (destroying the front, about −2 ∘C per 100 km × 10−7 s−1) in most parts of the ABFZ, except just near the coast at 17∘ S; although its frontogenetic (generating front) contribution is rather weak here (less than 2 ∘C per 100 km × 10−7 s−1). CONF has on average an intense frontogenetic contribution to the ABFZ (up to 5 ∘C per 100 km × 10−7 s−1), especially offshore around 16∘ S, the latitude where the ABFZ is centered (Fig. 2). The frontogenetic effect of CONF is consistent with GC2014 (the frontogenesis of the SST front associated with the equatorial Atlantic cold tongue is due to the confluence of the northern South Equatorial Current and Guinea Current) and can be expected because the warm and cold currents meet around the ABFZ. Note, however, a small zone just near the coast at 16∘ S where the CONF is frontolytic. This local frontolytic contribution is overcompensated by a strong frontogenesis due to TILT (more than 5 ∘C per 100 km × 10−7 s−1 on average in the ABFZ core). An elongated frontogenetic zone associated with TILT is found along the Angolan coast from 17 to 11∘ S and corresponds to the upwelling tongue observed in the Angola Current region (Fig. 3). On the other hand, TILT is frontolytic off the ABFZ (at 17∘ S, 11∘ E) where the downwelling is dominant as shown in Fig. 3. The role of the upwelling in the ABFZ development will be analyzed in more detail in Sect. 6.2.
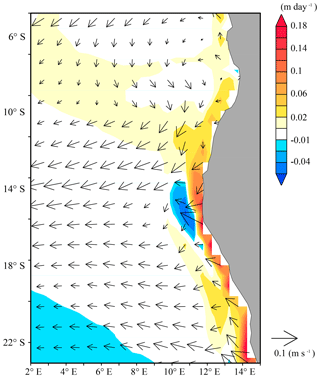
Figure 3Annual-mean climatological states of OML-mean horizontal current (arrows) and vertical velocity at the bottom of the OML (color).
In addition to the mechanical terms, the thermodynamical component also shows some influences on the ABFZ. SFLX works frontogenetically just near the coast at 16∘ S and frontolytically south and north from the core of the ABFZ; although its contribution is almost negligible compared to the mechanical contribution. Annual-mean climatology of RESD is estimated from Eq. (4) where the left-hand side is zero for climatology independent of time,
Note that all terms in Eq. (5) are for an annual-mean climatology. On average in the core of the ABFZ, RESD shows a strong frontolytic contribution around the core of the ABFZ (Fig. 4e). On the other hand, frontogenesis is located in the southern part of the ABFZ. This may be due to, at least partly, vertical mixing at the base of the OML accounted for in RESD. In particular, GC2014 showed that for the SST front associated with the equatorial Atlantic cold tongue, the turbulent mixing (surface and thermocline heat fluxes) is frontolytic.
5.2 Seasonal cycle
In the preceding subsection, we have shown that in terms of climatological annual-mean, CONF and TILT of the OFGF were the main sources for the ABFZ generation. Next, we analyze the annual cycle of the ABFZ and its relationship to the seasonal variations in the OFGF terms. As shown in Fig. 2, the seasonal cycle of the ABFZ exhibits two peaks. Note that if the seasonal cycle is sinusoidal, Eq. (4) implies π∕2 phase shift between the OFGF and temperature meridional gradient. This means that for a semiannual oscillation the temperature meridional gradient should lag the OFGF by approximately 1.5 months.
Figure 5a illustrates the box-mean (10–12∘ E and 17–15∘ S) time series of the meridional gradient of temperature obtained from satellite and reanalysis products (the time series is smoothed by a 11-day mean moving filter). This box covers the maximum of the ABFZ in each month since the meridional location of the ABFZ is almost stable in the climatological seasonal cycle. There is an obvious semiannual cycle of the ABFZ with maxima in April–May and in November–December, and minima in February–March and July–August (see also Fig. 2). The first maximum develops rapidly (during 2 months, from March to April), whereas the development of the second maximum is somewhat slower (3 months, from August to October). Figure 5a also evidences that CFSR realistically reproduces the semiannual cycle, although the magnitudes of the CFSR meridional SST gradient are generally slightly stronger with respect to OISST. Corresponding to the annual cycle of the ABFZ, there is a seasonal cycle of frontogenesis and frontolysis in Fig. 5a as the tendency of the ABFZ (green line): two maxima in frontogenesis in March–April and September–October and in frontolysis in May–June and December–February. The tendency of the ABFZ is estimated by Eq. (6).
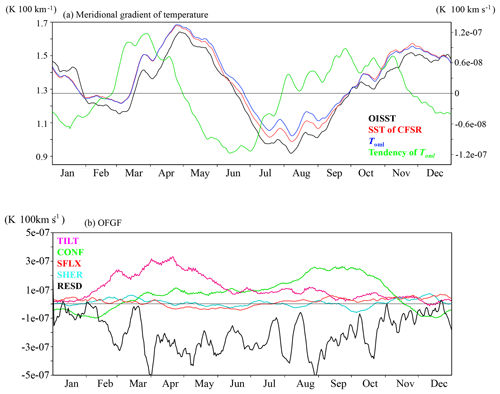
Figure 5Box-mean (17–15∘ S and 10–12∘ E) time series of (a) meridional gradient of temperature (black: OISST, red: SST of CFSR, and blue: OML-temperature of CFSR) and (b) TILT (magenta), CONF (green), SHER (cyan), SFLX (red), and RESD (black). Eleven-day running means are shown for all time series.
We further analyze the seasonal cycle of the OFGF terms. Similarly to the climatological state in Fig. 4, the contributions of SHER and SFLX are relatively small and do not seem to be responsible for either of the two peaks in the ABFZ annual cycle (not shown). Figure 5b shows the seasonal variations of TILT, CONF, and RESD averaged over the same box as the temperature gradients in Fig. 5a. For estimation of seasonal variation in RESD, the tendency of the meridional gradient is calculated as
where t and Δt denote each time step and difference in time step; in this case, Δt is 1 day (86 400 s). With this tendency at each day, RESD(t) is estimated by
From the middle of November to February, the box-averaged CONF is modestly negative, which is due to the frontolytic effect adjacent to the Angolan coast as shown in Fig. 4b (however, CONF is frontogenetic off the ABFZ). The contribution of CONF becomes positive from March, although its frontogenetic contribution is relatively weak (< 1.0 ∘C per 100 km × 10−7 s−1) until July. From the end of July CONF starts to increase and reaches its maximum (3.0 ∘C per 100 km × 10−7 s−1) at the end of August. The frontogenetic contribution of CONF remains strong until the beginning of October but then rapidly decrease to become frontolytic in November.
The contribution of TILT to the ABFZ seasonal cycle is almost always frontogenetic. Close to zero in January, TILT is enhanced from February and reaches its maximum value (3.0 ∘C per 100 km × 10−7 s−1) in March–April. In May–June, the frontogenetic effect of TILT gradually decreases (down to 1.0 ∘C per 100 km × 10−7 s−1) until December. The maxima in TILT and CONF correspond to the two periods of development of the ABFZ at the seasonal timescale: from March to April and from August to October, respectively (Fig. 5a). This suggests that the two peaks of the ABFZ are associated with two different mechanical terms and thus are due to two different physical processes. On the other hand, the two periods of decay of the ABFZ are consistent with the periods of weak frontogenetic and/or frontolytic contributions of both TILT and CONF (as observed by Mohrholz et al., 1999) in December–February and June–July, respectively.
In addition, RESD is almost always frontolytic with a relatively large oscillation (0.0 to −5.0 ∘C per 100 km × 10−7 s−1) as shown in Fig. 5b. In particular, the frontolytic effect due to RESD is stably strong (around −3.0 ∘C per 100 km × 10−7 s−1) from May–August when the ABFZ becomes weakened and frontogenetic effects due to CONF and TILT are relatively weak (Fig. 5a and b). In contrast with TILT and CONF, RESD does not exhibit a clear signal of semiannual cycle, but rather an annual cycle. We thus can conclude that in terms of a first-order estimation, the semiannual cycle of the ABFZ is explained by the combination of TILT and CONF.
The previous section showed that the two periods of development of the ABFZ in March–April and August–October were due, to a large extent, to the contribution of TILT and CONF, respectively. In this section, we investigate what components are responsible for the corresponding peaks in TILT and CONF.
6.1 Meridional confluence
CONF represents changes in the meridional temperature gradient associated with ocean dynamics of convergence or divergence of meridional current, . Figure 6a presents the annual cycle of averaged over the ABFZ. In the ABFZ, the meridional current is almost always convergent except for weak divergence from November to January. The convergence of the meridional current is maximum from August to mid-October (up to −3.0 × 10−7 s−1) and is rapidly weakened during November. The seasonal fluctuations in the convergence are associated with changes in intensity and meridional extension of the southward Angola Current and northward Benguela Current that meet in the ABFZ. Around the ABFZ, an area of lower SSH is formed, associated with the Angola Dome (the cold dome identified by Mazeika, 1967), which shows a pronounced seasonal cycle (e.g., Doi et al., 2007). Such well-organized SSH spatial variability induces the geostrophic current, which can contribute to the current system around the ABFZ. Therefore, here we also focus on the SSH and corresponding geostrophic current. Figure 6b illustrates the annual cycle of the OML-mean meridional current and meridional component of geostrophic current estimated from SSH at 15∘ S (north of the core of the ABFZ) and 17∘ S (south of the core of the ABFZ) averaged between 10 and 12∘ E. At 15∘ S the OML-mean meridional current is southward all year round, except for the beginning of May when a weak northward flow is observed. The maximum southward meridional velocity occurs in October (−0.12 m s−1). At 17∘ S the OML-mean meridional current is northward in March–June and shows a biannual peak of southward current in January to mid-February and October indicating intrusion of tropical warm water to the ABFZ (e.g., Rouault, 2012). Figure 6b clearly evidences that the region between 17 and 15∘ S is expected to be convergent. The most convergent period is in September–October when the CONF contribution to frontogenesis is the largest as shown in Fig. 5b. Another relatively strong convergent period is from April to June when the meridional current is rather northward at 17∘ S and close to zero at 15∘ S. The period of weak convergence or divergence, from December to February, corresponds to frontolytic contribution of CONF (Fig. 5b). Figure 6b evidences that the OML-mean meridional current can be explained, to a large extent, by the geostrophic surface current. While a large part of the meridional current and its seasonal cycle around the ABFZ is explained by geostrophic current associated with the SSH to the northwest of the ABFZ, there are some differences between voml and vg. These differences are due to the Ekman and ageostrophic currents.
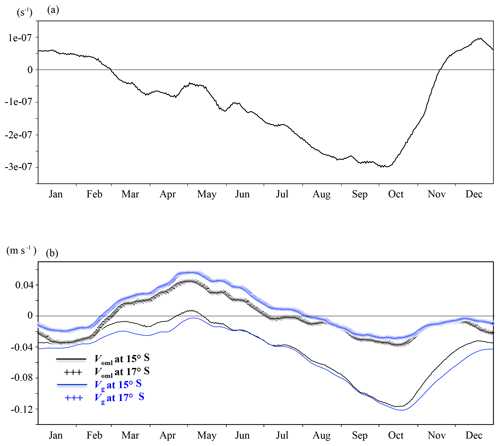
Figure 6Time series of (a) averaged over (17–15∘ S and 10–12∘ E) and (b) OML-mean meridional current velocity (black) and geostrophic meridional current velocity estimated from sea surface height (blue) at 15∘ S (solid line) and 17∘ S (+ mark) averaged between 10 and 12∘ E. All variables are filtered by a moving 11-day window.
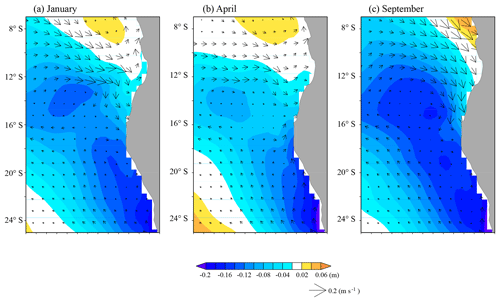
The spatial distributions of the climatological monthly-mean SSH and surface geostrophic current in January, April, and September are shown in Fig. 7. Two local minima of SSH are observed: one along the coast in the Benguela system and one west of the ABFZ (centered at 14∘ S and 6∘ E). The latter is associated with the Angola Dome (e.g., Doi et al., 2007) and a strong cyclonic geostrophic flow reaching the ABFZ. The geostrophic current generally generates the convergence in the ABFZ (Fig. 6a). However, in January an intense divergence is generated due to the strong southward ageostrophic current along the coast (Fig. 7a). In April, when CONF is modestly frontogenetic (Fig. 5b), the Angola Dome and associated geostrophic flow are diminished (Fig. 7b) and a main source of convergence can thus be attributed to the northward Benguela Current that penetrates into the ABFZ as far as 16∘ S. In September, although the low SSH sits in the south of the ABFZ as in April, the Angola Dome is significantly developed to be related to a strong geostrophic current resulting in a strong southward Angola Current intruding into the ABFZ along the Angolan coast. The northward Benguela Current is relatively weak in September compared to that in April. Thus, the maximum CONF in September is due to the strong southward Angola Current.
6.2 Tilting
TILT is the second main contributor to generate the ABFZ especially in March to May as shown in Figs. 4 and 5. In a first approximation, TILT results from the meridional gradient of vertical motion convoluted with the thermocline stratification (e.g., Eq. 4). Here, we explore more details of upwelling in the ABFZ. The annual cycle of these two components averaged over the box 12–10∘ E and 17–15∘ S (Fig. 8) points out the negative and the positive stratification from January to August, respectively. This configuration leads to frontogenesis through the TILT term (Fig. 5b). From August to December, changes sign and the stratification becomes weaker; that explains why the TILT term is frontolytic (especially in September) and its magnitude is weaker compared to January–August because of a weaker stratification (smaller vertical gradient in temperature). Negative can be seen in both March–April and August–September around the ABFZ in Fig. S1a and b in the Supplement, but positive are also generated around the ABFZ more in August–September than in March–April.
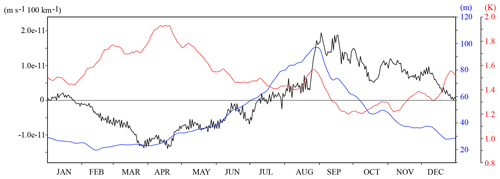
Figure 8Time series of the area-averaged meridional gradient of the vertical velocity at the bottom of OML (black), OML depth (blue), intensity of upper-ocean thermocline stratification (red) over 17–15∘ S and 10–12∘ E. All variables are filtered by a moving 11-day window.
The OML depth has extrema in August–September (around 100 m) and from January–April (around 20 m) indicating the seasonal cycle of solar insolation forcing and wind-driven mixing. Also, the intensity of the thermocline shows a strong stratification from March to May (2 ∘C) and weak stratification from September to November (1.2 ∘C). From March to May TILT is the most dominant frontogenetic source because the OML is the shallowest (20–30 m), the stratification is the strongest (temperature jump in the thermocline up to 2.0 K), and the shear of vertical velocity is strongly negative. The shallow OML and strong stratification can amplify the tilting effect due to . Conversely, TILT is weakly frontolytic from August to September when the OML depth is deepened (∼100 m), the stratification is weak (1.2 K), and is positive. Figure S1c and d shows the differences in OML depth and ocean stratification between March–April and August–September. Shallower OML and stronger stratification can be seen everywhere around the ABFZ. Therefore, effects of both positive and negative are reduced and consequently, the contribution of TILT is quite weak in August–September (Fig. 5b).
In this study we investigated the processes controlling the ABFZ evolution based on a first-order estimation of an ocean frontogenetic function (OFGF) applied to the ocean mixing layer (OML) derived from the CFSR reanalysis. The OFGF represents the temporal evolution of the meridional mixed-layer temperature gradient and contains three mechanical terms (shear, convergence and tilting) and one thermodynamical term. The residual term accounts for, in particular, vertical mixing at the bottom of the OML (which is based on parameterization of turbulence, i.e., highly nonlinear processes), entrainment velocity, and horizontal or vertical advection of the meridional temperature gradient. An analysis of the annual mean OFGF suggests that the confluence effect (CONF) due to southward Angola Current (warm) and northward Benguela Current (cold) is dominantly frontogenetic over the offshore part of the ABFZ, although it has a local frontolytic effect just near the coast at 16∘ S. The tilting effect (TILT) related to the coastal upwelling regime is another main contributor to frontogenesis. Around the ABFZ, intense Ekman transport divergence is generated by wind stress curl (Fig. S2). This Ekman divergence induces upward motion in the Ekman layer. Interestingly, the Ekman divergence due to the zonal wind stress is also an important contributor to the vertical velocity in the ABFZ. The contributions of the shear (SHER) and surface heat flux (SFLX) terms are rather negligible, while the residual (RESD) term represents a main frontolytic source.
Climatological seasonal evolution of the ABFZ has a well-pronounced semiannual cycle with two maxima of the SST meridional gradient, in April–May and November–December, and two minima, in February–March and July–August. We showed that the two maxima of the ABFZ were associated with two different mechanical terms and due to two different physical processes. The development of the first ABFZ maximum during March–April is mainly explained by the strong contribution of TILT to frontogenesis, while the development of the second ABFZ maximum during September–October is due to the frontogenetic contribution of CONF. TILT is associated with the meridional gradient of the vertical velocity. The annual maximum of TILT in March–April is due, to a large extent, to the combination of the maximum stratification (Δθ), shallow OML depth (D), and negative during this period. Indeed, in OFGF the ratio represents the efficiency by which the meridional gradient of the coastal upwelling velocity can lead to the change of the ABFZ intensity. Although the OML depth also modulates the surface heat flux contribution to the OFGF, the thermodynamical term does not show any significant impact on the development of the ABFZ maximum in March–April. On the other hand, the importance of the OML depth for the thermodynamical term was suggested for frontogenesis in a SST front associated with western boundary current (Tozuka and Cronin, 2014; Tozuka et al., 2018). The annual maximum of CONF in September–October is related to an intensified southward Angola Current that seems to be induced by an approximately cyclonic geostrophic flow associated with the development of the Angola Dome (e.g., Doi et al., 2007). However, the geostrophic current is not completely consistent with the OML-mean current. The difference can be attributed to the Ekman transport and ageostrophic component. A relatively smaller contribution of CONF to frontogenesis is also observed in April and is due to the intrusion of the northward Benguela Current to the ABFZ during this period.
Most CGCMs fail to reproduce realistic SST fields and ABFZ locations with respect to climatology. Among other causes, this can be due to a poor representation of regional climate variables in CGCMs (such as upwelling-favorable wind, wind drop off, and consequently near-coastal wind curl, alongshore stratification, and OML depth (e.g., Xu et al., 2014; Koseki et al., 2018; Goubanova et al., 2018), which directly impact the two main frontogenesis terms (CONF and TILT). The OFGF proposed in the present study can thus be an appropriate tool to diagnose the performance of CGCMs in the ABFZ and more generally in frontal zones. This study shows that diagnoses developed for mesoscale studies are valuable for climate studies and can help to identify the origin of biases that affect ocean general circulation models (OGCMs).
Although the present study focused on the climatological state of the ABFZ and its seasonal cycle, the intensity and the location of the ABFZ exhibits a strong interannual variability (e.g., Mohrholz et al., 1999; Rouault et al., 2017). Further investigation on how the contributions of the OFGF are modified in the case of the Benguela Niño/Niña would provide further insight into the dynamics of the southeastern tropical Atlantic and sources of the CGCMs bias that have been suggested to develop as interannual warm events (e.g., Xu et al., 2014).
Effects of the turbulent mixing and the effect due to the entrainment velocity at the mixed-layer base on frontogenesis were accounted for by the residual of the frontogenetic function. An accurate quantification of these effects requires using simulations of a higher resolution ocean model for which the output of the temperature tendency due to those processes are available. According to Giordani and Caniaux (2014), the vertical mixing is also a large contributor to the frontogenesis. However, by destroying the balance between the mass and circulation fields, the assimilation procedure induces spurious effects on the entrainment processes, which justifies that this process was included in the residual term RESD. These are the main limitations of this study because diapycnal mixing is often an important term of the oceanic upper-layers heat budget, which is tightly coupled with vertical motions (Giordani et al., 2013). A more comprehensive understanding of this term would be valuable to estimate the performance of CGCMs in the ABFZ and more generally in coastal upwelling zones.
The CFSR reanalysis data (Saha et al., 2010) used in this study can be downloaded from https://climatedataguide.ucar.edu/climate-data/climate-forecast-system-reanalysis-cfsr. The data of OISST (Reynolds, et al., 2007) are available at https://www.ncdc.noaa.gov/oisst.
The supplement related to this article is available online at: https://doi.org/10.5194/os-15-83-2019-supplement.
SK derived the ocean frontogenetic function (OFGF) by discussing with HG and KG and improved the OFGF. SK performed the main analysis of the data and all authors contributed to the interpretation of the results and discussion. SK wrote a first draft and HG and KG improved the draft extensively with constructive and critical comments on the draft.
The authors declare that they have no conflict of interest.
We greatly appreciate two anonymous reviewers for their constructive and
helpful comments. Also, we would like to express our appreciation to
Kunihiro Aoki in the University of Tokyo for his constructive discussion in
the initial stage of this study. We also thank Guy Caniaux in
Météo-France for their helpful discussions. We used the 2012Rb
versions of the MATLAB software package provided by MathWorks, Inc.,
(http://www.mathworks.com, last access: 13 August 2018) and Grid
Analysis and Display System (GrADS, http://cola.gmu.edu/grads/, last
access: 30 November 2018) to compute each dataset and create figures.
Shunya Koseki has received funding from the EU FP7/2007–2013 under grant
agreement no. 603521 (EU-PREFACE) and STERCP (ERC, grant no. 648982).
Katerina Goubanova was also supported by FONDECYT (grant 1171861).
Edited by: John M. Huthnance
Reviewed by: two anonymous referees
Astudillo, O., Dewitte, B., Mallet, M., Frappart, F., Rutllant, J. A., Ramos, M., Bravo, L., Goubanova, K., and Illig, S.: Surface winds off Peru-Chile: Observing closer to the coast from radar altimetry, Remote Sens. Environ., 191, 179–196, https://doi.org/10.1016/j.rse.2017.01.010, 2017.
Auel, H. and Verheye, H. M.: Hypoxia tolerance in the copepod Calanoides carinatus and the effect of an intermediate oxygen minimum layer on copecod vertical distribution in the northern Bengulea Current upwelling system and the Angola-Benguela Front, J. Exp. Mar. Biol. Ecol., 352, 234–243, 2007.
Chavez, F. P. and Messié, M.: A comparison of eastern boundary upwelling ecosystem, Prog. Oceanogr., 83, 80–96, 2009.
Chen, Z., Yan, X.-H., Jp, Y.-H., Jiang, L., and Jiang, Y.: A study of Bengulea upwelling system using different upwelling indices derived from remotely sensed data, Cont. Shelf Res., 45, 27–33, 2012.
Colberg, F. and Reason, C. J. C.: A model study of the Angola Benguela Frontal Zone: Sensitivity to atmospheric forcing, Geophys. Res. Lett., 33, L19608, https://doi.org/10.1029/2006GL027463, 2006.
Colberg, F. and Reason, C. J. C.: A model investigation of internal variability in the Angola Benguela Forntal Zone, J. Geophys. Res., 112, C07008, https://doi.org/10.1029/2006JC003920, 2007.
Dinniman, M. S. and Rienecker, M. M.: Frontogenesis in the North Pacific Ocean Frontal Zones-A Numerical Simulation, J. Phys. Oceanogr., 29, 537–559, 1999.
Doi, T., Tozuka, T., Sasaki, H., Masumoto, Y., and Yamagata, T.: Seasonal and interannual variations of oceanic conditions in the Angola Dome, J. Phys. Oceanogr., 37, 2698–2713, https://doi.org/10.1175/2007JPO3552.1, 2007.
Fennel, W., Junker, T., Schmidt, M., and Mohrholz, V.: Response of the Benguela upwelling system to spatial variations in the wind stress, Cont. Shelf Res., 45, 65–77, 2012.
Florenchie, P., Lutjeharms, J. E., Reason, C. J. C., Masson, S., and Rouault, M.: The source of Benguela Ninos in the South Atlantic Ocean, Geophys. Res. Lett., 30, 1505, https://doi.org/10.1029/2003GL017172, 2003.
Gammelsrød, T., Bartholomae, C. H., Boyer, D. C., Filipe, V. L. L., and O'Toole, M. J.: Intrusion of warm surface water along the Angolan-Namibian coast in February–March 1995: the 1995 Benguela Nino, S. Afr. J. Marine Sci., 19, 41–56, https://doi.org/10.2989/025776198784126719, 1998.
Giordani, H. and Caniaux, G.: Sensitivity of cyclogenesis to sea surface temperature in the Northwestern Atlantic, Mon. Weather Rev., 129, 1273–1295, 2001.
Giordani, H. and Caniaux, G.: Diagnosing vertical motion in the Equatorial Atlanitc, Ocean Dynam., 61, 1995–2018, https://doi.org/10.1007/s10236-01-0467-7, 2011.
Giordani, H., Caniaux, G., and Voldoire, A.: Intraseasonal mixed-layer heat budget in the equatorial Atlantic during the cold tongue development 2006, J. Geophys. Res., 118, 650–671, https://doi.org/10.1029/2012JC008280, 2013.
Giordani, H. and Caniaux, G.: Lagrangian sources of frontogenesis in the equatorial Atlantic front, Clim. Dynam., 43, 3147–3162, https://doi.org/10.1007/s00382-014-2293-3, 2014.
Goubanova, K., Illig, S., Machu, E., Garcon, V., and Dewitte, B.: SST subseasonal variability in the central Benguela upwelling system as inferred from satellite observation (1999–2009), J. Geophys. Res., 118, 4092–4110, https://doi.org/10.1002/jgrc.20287, 2013.
Goubanova, K., Sanchez, G., E., Frauen, C., and Voldoire A.: Role of remote and local wind stress forcing in the development of the warm SST errors in the southeastern tropical Atlantic in a coupled high-resolution model, Clim. Dynam., 2018.
Griffies, S. M., Harrison, M. J., Pacanowski, R. C., and Rosati, A.: Technical guide to MOM4, GFDL Ocean Group Technical Report No. 5, 337 pp., available at: https://www.gfdl.noaa.gov/-fms (last access: 15 November 2018), 2004.
Hanshingo, K. and Reason, C. J. C.: Modelling the atmospheric response over southern Africa to SST forcing in the southeast tropical Atlantic and southwest subtropical Indian Oceans, Int. J. Climatol., 29, 1001–1012, https://doi.org/10.1002/joc.1919, 2009.
Hastenrath, S. and Lamb, P.: On the dynamics and climatology of surface flow over the equatorial oceans, Tellus, 30, 436–448, 1978.
Hirst, A. C. and Hastenrath, S.: Atmopshere-Ocean Mechanisms of Climate Anomalies in the Angola-Tropical Atlantic Sector, J. Phys. Oceanogr., 13, 1146–1157, https://doi.org/10.1175/1520-0485(1983)013<1146:AOMOCA>2.0.CO;2, 1983.
Junker, T., Schmidt, M., and Mohrholz, V.: The relation of wind stress curl and meridional transport in the Benguela upwelling system, J. Mar. Res., 143, 1–6, 2015.
Junker, T., Mohrholz, V., Siegfired, L., and van der Plas, A.: Seasonal to interannual variability of water mass characteristics and current on the Namibian shelf, J. Mar. Syst., 165, 36–46, 2017.
Kay, E., Eggert, A., Flohr, A., Lahajnar N., Nausch, G., Nuemann, A., Rixen, T., Schmidt, M., Van der Pla, A., and Wasmund, N.: Biogeochemical processes and turnover rates in the Northern Benguela Upwelling System, J. Mar. Syst., 188, 63–80, 2018.
Kazmin, A. S. and Rienecker, M. M.: Variability and forntogenesis in the large-scale oceanic frontal zones, J. Geophys. Res., 101, 907–921, 1996.
Keyser, D., Reeder, M. J., and Reed, R. J.: A Generalization of Petterssens's Frontogenesis Function and Its Relation to the Forcing of Vertical Motion, Mon. Weather Rev., 116, 762–780, 1988.
Klein S. A. and Hartmann, D. L.: The Seasonal Cycle of Low Stratiform Clouds, J. Clim., 6, 1587–1606, 1993.
Koseki, S., Keenlyside, N., Demissie, T., Toniazzo, T., Counillon, F., Bethke, I., Ilicak, M., and Shen, M.-L.: Causes of the large warm SST bias in the Angola-Benguela Frontal Zone in the Norwegian Earth System Model, Clim. Dynam., 50, 4651–4670, https://doi.org/10.1007/s00382-017-3896-2, 2018.
Kopte, R., Brandt, P., Dengler, M., Tchipalanga, P. C. M., Macueria, M., and Ostrowski, M.: The Angola Current: Flow and hydrographic characteristic as observed at 11∘ S, J. Geophys. Res.-Oceans, 122, 1177–1189, https://doi.org/10.1002/2016JC012374, 2017.
Lutz, K., Jacobeit, J., and Rathmann, J.: Atlantic warm and cold water events and impact on African west coast precipitation, Int. J. Climatol., 35, 128–141, 2015.
Manhique, A. J., Reason, C. J. C., Silinto, B., Zucula, J., Raiva, I., Congolo, F., and Mavume, A. F.: Extreme rainfall and floods in southern Africa in January 2013 and associated circulation patterns, Nat. Hazards, 77, 679–691, https://doi.org/10.1007/s11069-015-1616-y, 2015.
Mazeika, P. A.: Thermal domes in the eastern tropical Atlantic Ocean, Limnol. Oceanogr., 12, 537–539, 1967.
Mohrholz, V., Schmidt, M., Lutjeharms, J. R. E., and John, H.-C. H.: Space-time behavior of the Angola-Benguela Frontal Zone during the Benguela Nino of April 1999, Int. J. Remote Sens., 25, 1400, https://doi.org/10.1080/01431160310001592265, 2004.
Moisan, J. R. and Niler, P. P.: The Seasonal Heat Budget of the North Pacific: Net Heat Flux and Heat Storage Rate (1950–1990), J. Phys. Oceanogr., 28, 401–421, 1998.
NCAR/UCAR Climate Data Guide: Climate Forecast System Reanalysis (CFSR), available at: https://climatedataguide.ucar.edu/climate-data/climate-forecast-system-reanalysis-cfsr, last access: 7 February 2019.
NOAA: Optimum Interpolation Sea Surface Temperature (OISST), available at: https://www.ncdc.noaa.gov/oisst, last access: 7 February 2019.
Pfeifroth, U., Hollmann, R., and Ahrens, B.: Cloud Cover Diurnal Cycles in Satellite Data and Regional Climate Model Simulations, Meteorologische Z., 21, 551–560, 2012.
Reynolds, R. W., Smith, T. M., Liu, C., Chelton, D. B., Casey, K. S., and Schlax, M. G.: Daily High-Resolution-Blended Analyses for Sea Surface Temperature, J. Clim., 20, 5473–5496, 2007.
Rouault, M., Florenchie, P., Fauchereau, N., and Reason, C. J. C.: South east tropical Atlantic warm events and southern African rainfall, Geophys. Res. Lett., 30, 8009, https://doi.org/10.1029/2002GL014840, 2003.
Rouault, M.: Bi-annual intrusion of tropical water in the northern Benguela upwelling, Geophys. Res. Lett., 39, L12606, https://doi.org/10.1029/2012GL052099, 2012.
Rouault, M., Illig, S., Lübbecke, J., and Koungue, R. A. I.: Origin, development and demise of the 2010–2011 Benguela Niño, J. Mar. Syst., 188, 39–48, https://doi.org/10.1016/j,jmarsys.2017.07.007, 2018.
Saha, S., Moorti S., Pan H.-L., Wu X., Wang, J., Nadiga, S., Tripp, P., Kistler, R., Woollen, J., Behringer, D., Liu, H., Stokes, D., Grumbine, R., Gayno, G., Wang, J., Hou, Y.-T., Chuang, H., Juang, H.-M. H., Sela, J., Iredell, M., Treadon, R., Kleist, D., Van Delst, P., Keyser, D., Derber, J., Ek, M., Meng, J., Wei, H., Yang, R., Lord, S., van den Dool, H., Kumar, A., Wang, W., Long, C., Chelliah, M., Xue, Y., Huang, B., Schemm, J.-K., Ebisuzaki, W., Lin, R., Xie, P., Chen, M., Zhou, S., Higgins, W., Zou, C.-Z., Liu, Q., Chen, Y., Han, Y., Cucurull, L., Reynolds, R. W., Rutledge, G., and Goldberg, M.: The NCEP Climate Forecast System Reanalysis, B. Am. Meteorol. Soc., 91, 1015–1058, https://doi.org/10.1175/2010BAMS3001.1, 2010.
Santos, F., Gomez-Gesteria, M., deCastro, M., and Alvarez, I.: Differences in coastal and oceanic SST trends due to the strengthening of coastal upwelling along the Benguela current system, Cont. Shelf Res., 34, 79–86, 2012.
Tozuka, T. and Cronin, M. G.: Role of mixed layer depth in surface frontogenesis: The Agulhas Return Current front, Geophys. Res. Lett., 41, 2447–2453, https://doi.org/10.1002/2014GL059624, 2014
Tozuka, T., Ohishi, S., and Cronin, M. G.: A metric for surface heat flux effect on horizontal sea surface temperature gradients, Clim. Dynam., 51, 547–561, https://doi.org/10.1007/s00382-017-3940-2, 2018.
Veitch, J. A., Florenchie, P., and Shillington, F. A.: Seasonal and interannual fluctuations of the Angola-Benguela Frontal Zone (ABFZ) using 4.5 km resolution satellite imagery from 1982 to 1999, Int. J. Remote Sens., 27, 987–998, https://doi.org/10.1080/01431160500127914, 2006.
Vizy, E. K., Cook, K. H., and Sun, X.: Decadal change of the south Atlantic ocean Angola-Benguela forntal zone since 1980, Clim. Dynam., 51, 3251–3273, https://doi.org/10.1007/s00382-018-4077-7, 2018.
Xu Z., Chang, P., Richter, I., Kim, W., and Tang, G.: Diagnosing southeast tropical Atlantic SST and ocean circulation biases in the CMIP5 ensemble, Clim. Dynam., 43, 3123–3145, https://doi.org/10.1007/s00382-014-2247-9, 2014.
Zuidema, P. et al.: Challenges and Prospects for Reducing Coupled Climate Model SST Biases in the Eastern Tropical Atlantic and Pacific Oceans: The US CLIVAR Eastern Tropical Oceans Synthesis Working Group, B. Amer. Meteorol. Soc., 97, 2305–2328, https://doi.org/10.1175/BAMS-D-15-00274.1, 2016.