the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Numerical modelling of the Caspian Sea tides
Evgueni A. Kulikov
Isaac V. Fine
The Caspian Sea is the largest enclosed basin on Earth and a unique subject for the analysis of tidal dynamics. Tides in the basin are produced directly by the tide-generating forces. Using the Princeton Ocean Model (POM), we examine details of the spatial and temporal features of the tidal dynamics in the Caspian Sea. We present tidal charts of the amplitudes and phase lags of the major tidal constituents, together with maps of the form factor, tidal range, and tidal current speed. Semi-diurnal tides in the Caspian Sea are determined by a Taylor amphidromic system with anticlockwise rotation. The largest M2 amplitude is 6 cm and is located in Türkmen Aylagy (called Turkmen Bay hereafter). For the diurnal constituents, the Absheron Peninsula separates two individual amphidromes with anticlockwise rotation in the north and in the south. The maximum K1 amplitudes (up to 0.7–0.8 cm) are located in (1) the south-eastern part of the basin, (2) Türkmenbaşy Gulf, (3) Mangyshlak Bay; and (4) Kizlyar Bay. As a result, the semi-diurnal tides prevail over diurnal tides in the Caspian Sea. The maximum tidal range, of up to 21 cm, has been found in Turkmen Bay. The strongest tidal currents have been located in the straits to the north and south of Ogurja Ada, where speeds reach 22 and 19 cm s−1, respectively. Numerical simulations of the tides using different mean sea levels (within a range of 5 m) indicate that spatial features of the Caspian Sea tides are strongly sensitive to changes in mean sea level.
Tides, one of the major drivers of oceanic motions, are formed by the tide-generating forces of the Moon and the Sun under the influence of Earth's rotation. Tides can be represented as the sum of two types of oscillations: (1) the co-oscillating tide, caused by a tidal exchange with adjacent basins, and (2) the independent tide, generated directly by the tide-generating forces (Defant, 1961). Co-oscillating tides dominate in marginal seas and are generated by tidal waves entering from an adjoining ocean or sea. In isolated inland seas (e.g. the Black Sea and the Baltic Sea), independent tides strongly prevail, as tidal waves from adjacent basins cannot significantly penetrate the sea (Medvedev et al., 2013, 2016; Medvedev, 2018). The Caspian Sea is a unique subject for the analysis of independent tide formation as it is the largest fully enclosed basin on Earth.
Tides in the Caspian Sea have been studied for a long time, although not on a regular basis. Malinovsky (1926) showed that semi-diurnal tides dominate the Caspian Sea and that the spring tidal range was 7.7 cm, based on an analysis of 30 d records of hourly water levels from three tide gauges. German (1970) performed a spectral analysis of 3-month observational series at eight tide gauges and distinguished the diurnal and semi-diurnal constituents through different generation mechanisms; semi-diurnal tides had a gravitational origin, while diurnal tides were formed by sea-breezes. Kosarev and Tsyganov (1972) found the maximum tidal range to be 12 cm at Ogurja Ada (Fig. 1). Spidchenko (1973) estimated the amplitudes and phase lags at seven sites, and they found the mean spring tidal range to be 8.3 cm at Krasnovodsk. Analysing annual series of hourly observations at six tide gauges, Levyant et al. (1994) hypothesised that the semi-diurnal tidal wave is represented by a anticlockwise-rotating Kelvin-wave type amphidromic system with its centre in the area of the Absheron Threshold.
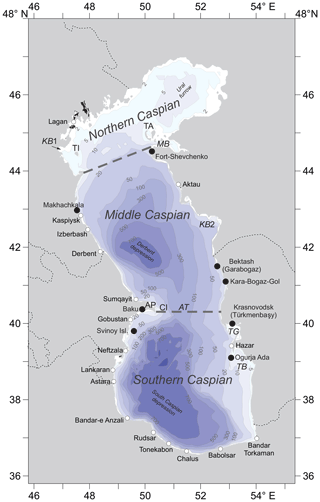
Figure 1The bathymetry of the Caspian Sea according to the GEBCO database. Numbers on the contours indicate the depths below mean sea level (MSL), which is −28 m with respect to the Baltic Height System (BHS). Black points denote sites of tide gauges used for validation of the numerical model. Other designations are given: TI is Tyulen'i (Tyuleny) island, TA is the Tyulen'i (Tyuleniy) archipelago, MB is Mangyshlak bay, KB1 is Kizlyar bay, KB2 is Kazakh bay, AP is the Absheron Peninsula, AT is the Absheron Threshold, CI is the Chilov (Zhiloy) island, TG is Türkmenbaşy Gulf, and TB is Turkmen Bay.
Medvedev et al. (2017) estimated the amplitudes and phase lags of major tidal constituents for different parts of the Caspian Sea based on analysis of long-term hourly data from 12 tide gauges. A maximum tidal range of 21 cm was found at Aladga (eastern part of the Southern Caspian). Medvedev et al. (2017) also performed a high-resolution spectral analysis and determined that the diurnal sea level oscillations in the Middle Caspian have a gravitational origin, while those in the Southern Caspian are mainly caused by radiational effects (the amplitude of the diurnal radiational constituent S1 is much higher than those of the gravitational constituents O1, P1, and K1). In the Northern Caspian, there are no gravitational tides and only weak radiational tides are observed. The semi-diurnal tide dominates the Middle Caspian and Southern Caspian regions.
Analyses of the tide gauge data allow for the examination of specific tidal features at different sites but not for the estimation of the spatial structure of tides in the deep-water areas of the Caspian Sea. Therefore, in order to capture these spatial structures we used the numerical Princeton Ocean Model (POM) adapted for the Caspian Sea (see Medvedev et al., 2019). The adapted POM reproduces the tides and meteorological sea level variability for periods ranging from several hours to a month. In the present paper, we use this model to characterise the spatial and temporal properties of the tidal dynamics for the entire Caspian Sea.
2.1 Numerical model description
The tidal motions examined in this study are based on a 2-D version of the Princeton Ocean Model (Mellor, 2004). The forcing term in the two-dimensional shallow-water equations is specified through gradients in the tidal potential over the Caspian Sea:
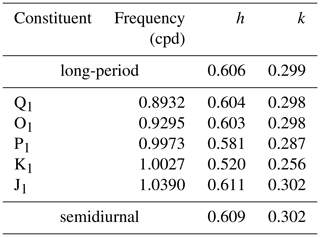
where is the tidal potential and k and h are the Love numbers, which relate the body Earth tide (and associated perturbations) to the potential. We used frequency-dependent values of h and k calculated by Wahr (1981) (Table 1). The tidal potential was calculated for spherical harmonics via formulae provided by Munk and Cartwright (1966) and included all the main tidal components (> 80), including the major diurnal, semidiurnal, and long-period constituents. Additionally, our numerical model includes the ocean tidal loading potential obtained from FES2014 (Finite Element Solution tidal model), produced by NOVELTIS, LEGOS, and CLS Space Oceanography Division and distributed by AVISO, with support from Centre National D'Etudes Spatiales (CNES) (http://www.aviso.altimetry.fr/, last access: 20 November 2019).
Table 1Love numbers for the major tidal constituents (Wahr, 1981; Kantha and Clayson, 2000). “cpd” is cycles per day.
In the numerical model, energy dissipation is through the vertical component of turbulent viscosity. The frictional force in the momentum equations is determined by the speed of the bottom flow and the friction coefficient:
where is the flow velocity above the bottom boundary layer (which is assumed to be equal to the barotropic velocity for the 2-D model), and Cb is the bottom friction coefficient, which has the following form:
where κ=0.4 is the von Kármán constant and z0 is the bed roughness length. A minimum value for the bottom friction coefficient, Cb=0.0025, was applied in order to avoid a vanishing bottom drag in very deep water.
The numerical simulations were performed on a grid of 507 by 659 nodes with a step of 1 arcmin in latitude and longitude, created from the General Bathymetric Chart of the Oceans (GEBCO) bathymetry data of the Caspian Sea with a resolution of 30 arcsec. For this region, GEBCO uses the gridded data set provided by Hall (2002). This dataset is based on over 280 000 bathymetric soundings digitised from bathymetric contours, taken from 107 Russian navigational charts. In Sect. 3.1, a mean sea level (MSL) for the Caspian of −28 m with respect to the Baltic Height System (BHS, relative to the zero level of the Kronstadt tide gauge) was adopted in the numerical modelling. In the numerical experiments in Sect. 3.4, the MSL of the Caspian was varied from −25 to −30 m with respect to the BHS. The boundary conditions for the tidal model are zero flow normal to the coast (at the 2 m depth contour).
2.2 Tidal model validation
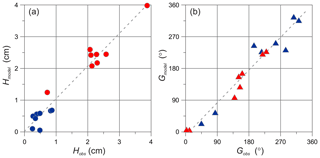
In Medvedev et al. (2019), the model results for the Caspian Sea were validated using hourly sea level observations from eight tidal gauges (Fig. 1). Several experiments with different values of the bed roughness length were performed. The best tide reproduction accuracy at the eight sites was obtained for z0=0.01 m, which is used in Eq. (3) to determine the bottom friction coefficient, Cb. Figure 2 presents a comparison of the amplitudes (H) and phase lags (G) of the tidal constituents calculated from the results of numerical modelling with those based on observations. The error in the calculations of the amplitude of the M2 harmonic at Baku, Svinoy island, Fort-Shevchenko, Garabogaz (called Bektash hereafter), and Ogurchinsky island (Ogurja Ada) did not exceed 0.1–0.2 cm. The corresponding errors for Kara-Bogaz-Gol and Krasnovodsk were 0.3–0.4 cm. The phase lag error for six of the tide gauges varied from 0 to 6∘, while for Ogurchinsky island it reached 36∘, and for Krasnovodsk it was 26∘. The amplitude error of the K1 harmonic at seven of the tide gauges was 0.1–0.2 cm and for Baku it was 0.4 cm. The phase lag errors varied from 1 to 50∘. All phase lags are relative to Greenwich, using Coordinated Universal Time (UTC).
3.1 Numerical modelling of tides
A numerical model with a MSL of −28 m with respect to the BHS was used. Amplitudes and phase lags of the major tidal constituents were calculated using classical harmonic analysis (Pugh and Woodworth, 2014). In this section, we examine the spatial pattern of diurnal and semi-diurnal tides taking the major constituents K1 and M2 as examples.
The diurnal tidal pattern includes a complicated amphidromic system in the Middle Caspian (Fig. 3a). The Absheron Peninsula splits this system into separate north and south amphidromes. Both amphidromic systems feature a anticlockwise rotation. Near the Absheron Peninsula, the K1 amplitude is less than 0.15 cm. The maximum K1 amplitudes (up to 0.7–0.8 cm) are located in (1) the south-eastern part of the Caspian Sea, (2) Türkmenbaşy Gulf, (3) Mangyshlak Bay, and (4) Kizlyar Bay. The second anticlockwise-rotating amphidrome is formed in the Northern Caspian. Medvedev et al. (2019) showed that the numerical modelling results are not very reliable in the Northern Caspian due to the shallow depths, with about 20 % of this part of the Caspian Sea being less than 1 m deep (Baidin and Kosarev, 1986). Other diurnal tidal constituents have a spatial distribution similar to that of K1. The amplitudes of these constituents are up to 0.5 cm for O1 and 0.25 cm for P1. The amplitudes of the other diurnal tidal constituents in the Caspian Sea do not exceed 0.1 cm.
Table 2Amplitudes (H) and Greenwich phase lags (G) of the major tidal constituents, form factor (F), and maximum tidal range (R) at the main cities in the Caspian Sea.
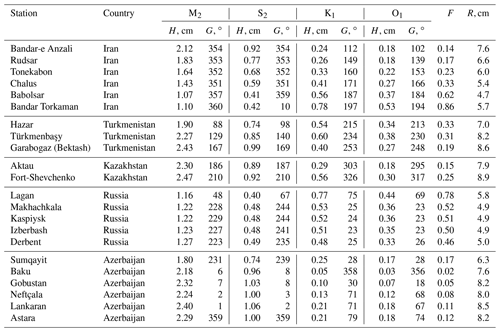
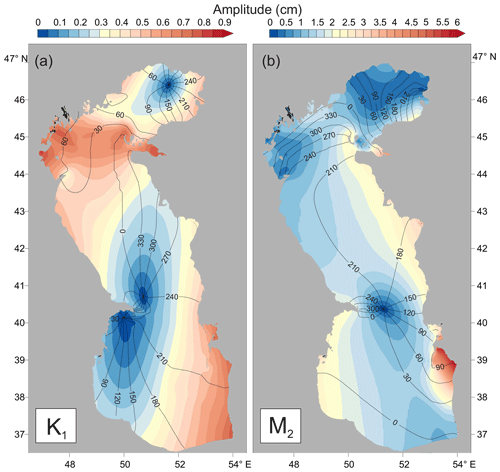
Figure 3Tidal maps of the co-amplitudes (cm) (shaded) and co-phase lags (degrees, UTC) (solid lines) for the (a) K1 and (b) M2 tidal constituents.
Semidiurnal tides in the Caspian Sea are determined by a Taylor amphidromic system with anticlockwise rotation (Fig. 3b). The amphidromic point of this system is located 80 km east of the Absheron Peninsula. The minimum M2 amplitudes are located (1) east of the Absheron Peninsula, (2) in the western part of the Northern Caspian, and (3) in the eastern part of the Northern Caspian. Maximum M2 amplitudes are found in (1) the western part of the Southern Caspian, up to 2.4 cm; (2) Kazakh Bay, up to 3.2 cm; (3) Mangyshlak Bay, up to 3.2 cm; and (4) the Türkmenbaşy Gulf, up to 3.9 cm. The largest M2 amplitude of 6 cm is located in Turkmen Bay. Other semi-diurnal tidal constituents have a similar spatial distribution to M2. The S2 amplitude in Turkmen Bay is 2.6 cm, N2 is 1.1 cm, and K2 is 0.7 cm. The amplitudes and phase lags of the major tidal constituents at selected towns around the Caspian Sea are presented in Table 2.
3.2 Form factor, tidal range, and role of tidal oscillations in sea level variability
The results of our analysis indicate that semi-diurnal tides prevail over diurnal tides in the Caspian Sea. To show this, we estimated the form factor as determined by the amplitude ratio of the major diurnal and semi-diurnal constituents (Pugh and Woodworth, 2014):
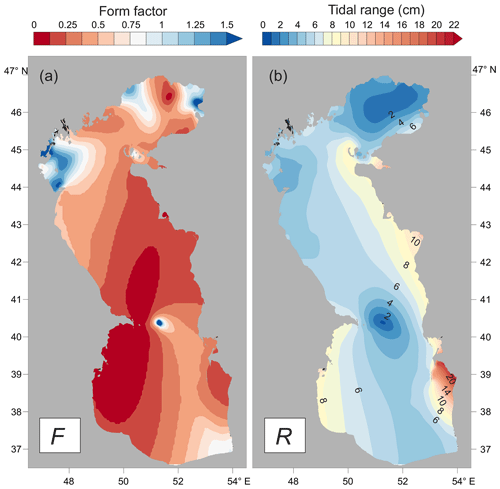
Tides have a semi-diurnal form in the eastern part of the Middle Caspian (F < 0.25), in the western part of the Southern Caspian (F < 0.25), and in Turkmen Bay (F ∼0.14) (Fig. 4a). In general, a mixed mainly semi-diurnal tide (0.25 < F < 1.5) is observed in other areas of the Caspian Sea. Only in the western and eastern parts of the Northern Caspian and at the semi-diurnal amphidromic point (80 km east of the Absheron Peninsula) does the tide have a mixed mainly diurnal form (F > 1.5).
Using the results of the numerical modelling of the diurnal, semi-diurnal, and shallow tidal constituents, we were able to predict an 18.6-year tidal time series at each grid node. The tidal range was calculated as the maximum range of the tidal sea level oscillations during one lunar day (∼25 h). The tidal co-range distribution features a pattern similar to the M2 amplitude distribution (Fig. 4b). The maximum tidal ranges are found for (1) Kazakh Bay, up to 12 cm; (2) Mangyshlak Bay, up to 12 cm; (3) Türkmenbaşy Gulf, up to 13 cm; and (4) Turkmen Bay, up to 21 cm. The form factor and tidal range at the main cities in the Caspian Sea are included in Table 2. Fort-Shevchenko features the largest tidal range listed in Table 2. The maximum tidal range for the Caspian Sea, as a whole, is observed in Turkmen Bay (21 cm), but there are no big cities in this area.
Medvedev et al. (2017) estimated the role of tidal oscillations in the overall sea level variability in the Caspian Sea by calculating the relative contribution of the tides (gravitational and radiational) to the total sea level variance in the frequency band from 0.5 to 6 cpd (cycles per day) for 11 tide gauges. The maximum contribution was observed at Bektash (27 %). At Aladga, which has the greatest range of 21 cm, the tidal contribution to the sea level variance was 22.5 %. The smallest relative contribution of the tides was found on the western coast: 7.6 % at Makhachkala and 11.7 % at Baku.
For this study, we estimated the contribution of the gravitational tides to the sea level variance based on the new numerical modelling results. We made two numerical experiments: (1) with the tides alone and (2) with meteorological forcing alone produced by variations in the wind and air pressure fields over the Caspian Sea for 1979 from NCEP/CFSR reanalysis (Saha et al., 2010). We calculated the variance of tidal sea level variability (excluding the long-period constituents) and the variance of the meteorological sea level variations in the frequency band from 0.1 to 6 cpd. Then, we estimated the relative contribution (in percent) of the tides to the total sea level variance in the Caspian Sea.
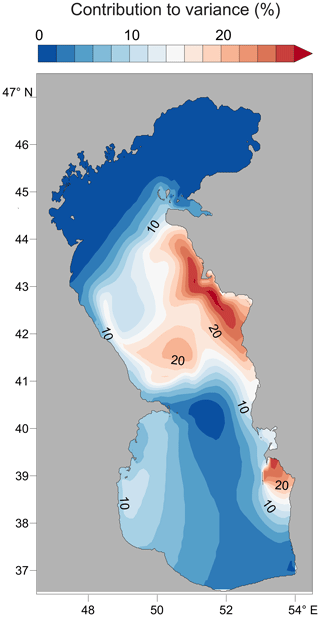
Figure 5The relative contribution (in percent) of the tides to the total sea level variance in the Caspian Sea in the frequency band from 0.1 to 6 cpd.
The maximum contribution of tides to the total sea level variance was found to be located in the eastern part of the Middle Caspian: up to 29 %. In Turkmen Bay, the tidal contribution to the total variance is up to 27 %. The minimum contribution is found in the Northern Caspian, where strong storm surges occur; and near the Absheron Peninsula, where the amphidromic points of the diurnal and semi-diurnal tides are located. The results of this analysis show that tides are a significant component of the overall sea level variability of the Caspian Sea in the mesoscale. Consequently, knowledge of the tidal characteristics is important for understanding the hydrodynamics of the sea.
Figure 6Semi-major axis speed magnitudes (cm s−1) for the M2 tidal currents. Blue ellipses indicate clockwise circulation, red ellipses anticlockwise circulation. Other designations: TA is the Tyulen'i archipelago, CI is the Chilov (Zhiloy) island, TG is Türkmenbaşy Gulf, TB is Turkmen Bay, OA is the Ogurja Ada.
3.3 Tidal currents
Tidal dynamics are characterised not only by sea level oscillations but also by periodic currents. The spatial structure of the amplitudes of the semi-major axes of tidal currents (Fig. 6) differs from the pattern of the tidal sea level amplitude distribution. The largest M2 current speeds (semi-major axis) are found in (1) Mangyshlak Bay near the Tyulen'i archipelago, up to 6.5 cm s−1; (2) Absheron Strait, which separates the Absheron Peninsula from the Chilov island, up to 7.5 cm s−1; and (3) in the straits to the north and south of Ogurja Ada, up to 12.5 and 11.7 cm s−1. The M2 ellipse parameters (semi-major and semi-minor axes amplitudes, the direction of maximum current speed, phase lags) change depending on local topographic features. For the highest speeds, the rotation of the ellipse occurs in a clockwise direction. In straits and in shallow waters (for example, in Turkmen Bay), the semi-minor axis approaches zero and the tidal currents are nearly rectilinear. The spatial pattern of the S2 tidal currents in the Caspian Sea has the same structure as that for the M2 constituent; the amplification areas and the ellipse parameters remain the same, only the S2 semi-major axis is half of that of M2. Since M2 and S2 have the highest current speeds in the Caspian Sea, the spatial pattern of the maximum total tidal currents, calculated from time series computed for 18.6 years, also repeats the pattern of the M2 constituent. On average, the maximum total tidal current speed in the Caspian Sea exceeds the M2 speed by a factor of 1.8. The highest speed of the total tidal currents is observed mainly in the following straits: (1) Mangyshlak Bay near the Tyulen'i archipelago, up to 11.5 cm s−1; (2) Absheron Strait, which separates the Absheron Peninsula from the Chilov island, up to 13 cm s−1; and (3) in the straits to the north and south of Ogurja Ada, up to 22 and 19 cm s−1.
3.4 Numerical experiments with varying MSL
Interannual variability in the MSL is one of the main features of interest in the hydrological regime of the Caspian Sea (Bolgov et al., 2007) (Fig. 7). The mean depth of the Northern Caspian is about 5–6 m. As a result, changes of the Caspian MSL by 2–3 m (as observed, for example between 1977 and 1994) lead to significant changes in the hydrodynamics of the Northern Caspian as well as in coastal waters of the Middle Caspian and Southern Caspian. MSL variations lead to changes in the area and volume of the sea, and they result in changes in the frequency-selective properties of both the entire Caspian Sea and its individual parts. As a consequence, the spatial characteristics of natural oscillations of the basin (seiches) and the tidal pattern should also be expected to change.
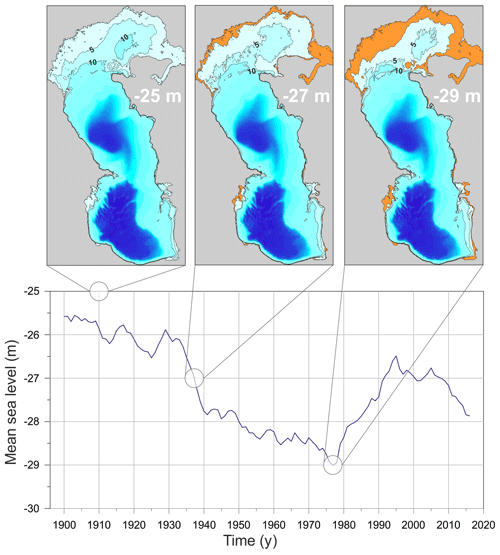
Figure 7Changes in the mean sea level (MSL) of the Caspian Sea at Makhachkala and the bathymetry of the sea for MSL values of −25, −27, and −29 m with respect to the BHS. Numbers on the contours indicate the depths of the shallowest areas below MSL in each case. Orange areas became dry as a result of the assumed MSL changes below −25 m.
For the present study, we conducted numerical experiments with tidal simulations using different MSL values of the Caspian Sea ranging from −25 to −30 m with respect to the BHS. This corresponds to the natural range of MSL changes in the Caspian Sea under climatic conditions typical for the sub-Atlantic climatic interval of the Holocene epoch (Bolgov et al., 2007). The results of these experiments allow us to identify changes in the Caspian Sea tidal patterns throughout the 19th and 20th centuries. The numerical results reveal that MSL changes over these two centuries led to a significant restructuring of the spatial structure of the natural sea level oscillations over the entire sea and its individual parts (specifically, the Middle Caspian and Southern Caspian).
The spatial structures of the semi-diurnal and diurnal tides in the Caspian Sea are modified by changes in the MSL (Fig. 8). The M2 amphidromic point shifts eastward by about 10 km with a decrease in the MSL from −25 to −29 m, leading to a general displacement of the area with amplitudes of 1.5–2 cm also to the east. As a result, the M2 amplitude decreases by 0.2–0.3 cm (up to 10 %–20 % of amplitude) along almost the entire eastern shore of the Middle Caspian. In the Southern Caspian, the tidal amphidrome also shifts to the east and the tidal amplitudes increase along the western coast. An area of amplification of the semi-diurnal tides with amplitudes of up to 6.5 cm is formed in Mangyshlak Bay (Northern Caspian) with the MSL of −25 m. When the MSL drops to −28 m, the semi-diurnal amplitude in this bay decreases to 3.2 cm.
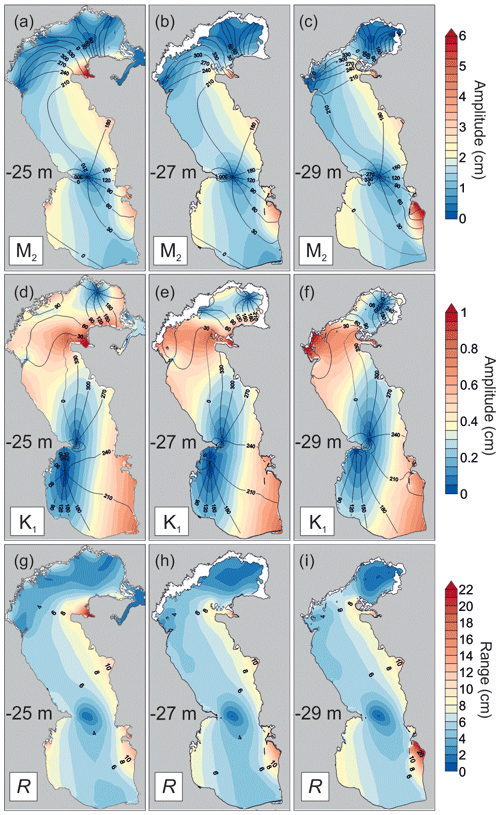
Figure 8Tidal maps for the amplitude of the M2 constituent (a, b, c), K1 (d, e, f), and tidal range (g, h, i) with different MSL values for the Caspian Sea: −25 m (a, d, g), −27 m (b, e, h), −29 m (c, f, i).
The most interesting and complex modification of the tidal pattern occurs on the east coast of the sea. In the Türkmenbaşy Gulf, the amplitude decreases from 4.4 cm with a MSL of −25 m to 3.1 cm for a MSL of −29 m. The reverse picture is observed in Turkmen Bay, where the amplitude increases from 3.5 to 6.5 cm. Turkmen Bay is a shallow semi-enclosed bay, with Ogurja Ada situated on its western border. This island is a narrow sandy spit approximately 42 km long and 1–1.5 km wide. The island's height currently does not exceed 3–5 m (Badyukova, 2015). Thus, when the MSL of the Caspian Sea is −25 m, a significant part of the island is submerged. Results of our numerical experiments show that the presence of the island creates a western boundary in Turkmen Bay. The formation of this boundary leads to a change in the frequency response of the bay and, as a consequence, to an increase in the amplitude of the semi-diurnal tides.
More pronounced modifications occur in the diurnal tide pattern with the MSL changes. For a MSL of −25 m with respect to the BHS, there is a more noticeable separation of the amphidrome near the Absheron Peninsula into two separate systems to the north-east and south of the peninsula. The amplitude of the diurnal tide on the western coast of the Southern Caspian is 0.1–0.15 cm higher (up to 50 % in amplitude) for a MSL of −29 m than for a MSL of −25 m. On the eastern coast of the Southern Caspian, the K1 amplitude varies weakly with the MSL changes (by 10 %). However, the K1 phase lags are modified. This is caused by the influence of Ogurja Ada at low MSL.
Strong modifications of the diurnal tidal pattern due to MSL changes occur along the transition between Northern Caspian and Middle Caspian. For a MSL of −25 m, the largest amplitudes are located near the Tyulen'i archipelago (up to 0.7–0.8 cm) and in Mangyshlak Bay (up to 1 cm). With decreasing MSL, large amplitudes extend farther west. For a MSL of −29 m, maximum amplitudes of up to 1.1 cm are already reached at the western coast of the Northern Caspian (near the Tyulen'i island). These changes are probably caused by a strong modification of the water depth of the shallow Northern Caspian and, as a result, of the frequency (resonant) properties of this subbasin.
The change in the spatial structure of the tidal range with changes in MSL is similar to that for the M2 amplitude pattern. The maximum tidal range of 22 cm is found in Mangyshlak Bay for a MSL of −25 m. At this MSL, the tidal range in Turkmen Bay is 13 cm and in Türkmenbaşy Gulf it is 15.5 cm. When the MSL decreases, the tidal range in Mangyshlak Bay decreases, while that in Turkmen Bay increases. For a MSL of −29 m, the tidal range in Turkmen Bay becomes 23 cm, whereas it is only 14 cm in Mangyshlak Bay.
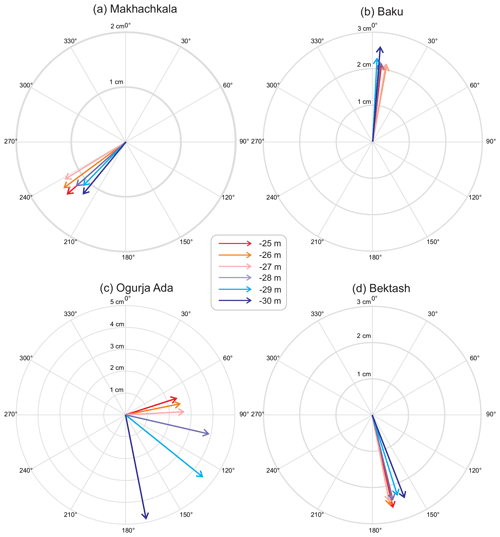
Figure 9Changes in the amplitude (cm) and phase lag (degrees) of the M2 tidal constituent at four sites with different values of the MSL based on numerical modelling results.
The changes in tidal characteristics can be very significant at individual sites. Figure 9 shows tidal vector diagrams that display the M2 model amplitude and phase lag for different sites for different MSL scenarios for the Caspian Sea. The amplitude and phase lag changes are relatively small at Makhachkala, Baku, and Bektash. However, the M2 phase lag for Ogurja Ada changes by about 100∘ and the M2 amplitude doubles: from 2.5 cm for a MSL of −25 m to 5 cm for a MSL of −30 m.
The results of the numerical tidal modelling in this study are in good agreement with the results of a harmonic analysis of tide gauge data of the Caspian Sea (Medvedev et al., 2017). Medvedev et al. (2017) demonstrated that a diurnal peak is absent in the sea level spectra on the western coast of the Southern Caspian (Baku, Svinoy island), which is confirmed here by the result of the numerical simulation of the K1 amplitude (Fig. 3a). Diurnal tides in the Southern Caspian are radiational and are formed under the influence of sea-breeze winds (Medvedev et al., 2017).
An unexpected result was obtained for the eastern part of the Southern Caspian. With a high MSL (for example, −25 m) a significant part of the territory of Ogurja Ada is below the mean water level. As a result, it is easier for tidal waves to penetrate Turkmen Bay. With a low MSL (for example, −29 m), the area and length of the island increase significantly, and the island becomes an effective boundary to the west, reflecting the tidal waves that penetrate Turkmen Bay. According to Badyukova (2015), the island's height currently does not exceed 3–5 m (MSL of −27.5 m with respect to the BHS). According to elevation data derived from the Shuttle Radar Topography Mission (SRTM; Farr et al., 2007), the island's maximum height is also 5–8 m. We used the GEBCO database to create our numerical grid for the model, with a maximum elevation of the island of 2 m at a MSL of −28 m. Thus, in the experiments assuming a MSL of −25 m, the island was completely submerged. However, according to historical records in 1835, when the MSL of the Caspian Sea was −25.5 m, the central elevated part of the island was in fact not flooded by the sea (the maximum height being about 3.5 m). Therefore, there is some modelling uncertainty about this aspect. According to Badyukova (2015), the island actually represents preserved fragments of a coastal delta plain which was built on transgressive coastal bars and subsequently merged into one island. A comparison of the island's coordinates in 1850 with 2013 (Badyukova, 2015) shows that the island has gradually moved eastward and has changed its geometrical configuration due to the redistribution of deposits and erosion. The greatest contribution to this process originates from aeolian redistribution. According to Nikiforov (1964), for each 1 m of the beach 5 kg of sand is carried inland every hour for a wind speed of 4.9 km s−1.
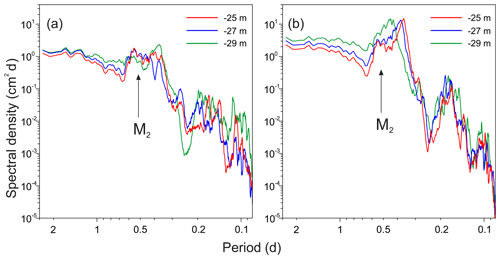
Figure 10Sea level spectra for (a) Türkmenbaşy Gulf and (b) Turkmen Bay at different MSL values for the Caspian Sea.
Numerical experiments were conducted with forcing produced by synthetic wind fields in order to assess changes in natural oscillations (seiches) with a change in the MSL. The magnitude and direction of the generated wind fields was varied randomly every 6 h. A spectral analysis of the simulated wind sea level variability showed that a decrease in the MSL leads to a change in the period and Q factor of the natural oscillations of Türkmenbaşy Gulf and Turkmen Bay. When the MSL of the Caspian Sea decreases, the Q factor of seiches in Türkmenbaşy Gulf, which have a period of about 12 h (i.e. around the M2 tidal period), significantly decreases. For a MSL of −29 m, this spectral peak does not exceed the spectral noise level (Fig. 10a).
In Turkmen Bay, a decrease in MSL from −26 to −29 m causes the spectral peak of the main seiche mode to migrate towards lower frequencies. Thus, the period of this seiche mode approaches the period of the M2 tidal constituent (Fig. 10b). This is due to the progressive elongation of Ogurja island, which represents the western boundary of the bay. The closeness of the period of natural oscillations (seiches) to the tidal period (12.42 h) affects the structure of the tidal oscillations. The “sensitivity” of the tides to the changes in the MSL is determined by the proximity or distance from the natural period.
In this numerical modelling study, we have investigated the tidal dynamics of the Caspian Sea. The numerical simulations were forced by the direct action of the tidal potential. The main objective of the study was to map the tidal characteristics of the Caspian Sea. For the first time, it has been possible to construct detailed co-tidal maps of the sea level and current ellipses for the major tidal constituents using a numerical hydrodynamic model taking into account data from long-term sea level observations. The results of the numerical simulations indicate that maximum tidal amplitudes are located in the south-eastern part of the sea. The contribution of the tides to the overall sea level variance in the frequency band from 0.1 to 6 cpd is up to 29 % in the eastern part of the Middle Caspian and up to 27 % in Turkmen Bay. We have shown that tidal currents can reach more than 20 cm s−1 in certain areas (for example, in straits), which is comparable to the magnitude of persistent currents due to the hydrological regime (Tuzhilkin and Kosarev, 2005). Our results indicate that the role of tides in the hydrodynamics of isolated (non-tidal) seas might have been previously underestimated.
Our numerical experiments demonstrate that the spatial features of the tides are sensitive to changes in the MSL. Modifications to the tidal pattern are caused by changes in the bathymetry and geometry of the coastline of shallow areas of the sea, including the Northern Caspian, which results in significant changes in the frequency response of the basin. This is also confirmed by changes in the natural oscillation (seiche) structure of the Caspian Sea.
In recent decades, significant progress has been achieved in the improvement of global barotropic tide models. This progress has been supported by satellite altimetry. Stammer et al. (2014) presented a detailed comparison of the main modern global barotropic tide models. Most of these models (FES14, EOT11a, TPXO9, GOT4.10, OSU12, DTU10, HAMTide) do not include the Caspian Sea.
We believe that our findings concerning tidal dynamics can help to better understand the diurnal and semi-diurnal variability in sea level and currents in the Caspian Sea. In addition, we suggest that our findings should be taken into account when future global tide models are constructed.
The model output data are published at the public data repositories of the Shirshov Institute of Oceanology, Russian Academy of Sciences; https://doi.org/10.29006/datasets.2020.cst.1 (Medvedev et al., 2020).
The concept of the study was jointly developed by IM and EK. IM did the numerical simulations, analysis, visualisation, and article writing. EK prepared the numerical grids and participated in the analyses and the interpretation of the results. IF adapted the numerical Princeton Ocean Model (POM) to the Caspian Sea and participated in the verification stage. IM prepared the paper with contributions from EK and IF.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Developments in the science and history of tides (OS/ACP/HGSS/NPG/SE inter-journal SI)”. It is not associated with a conference.
The authors would like to thank Richard Thomson, Philip Woodworth, Rosanna Neuhausler, and two anonymous reviewers for their very interesting comments and helpful suggestions during the preparation of the paper.
This research has been supported by the state assignment of IO RAS (grant no. 0149-2019-0005) and the Russian Foundation for Basic Research (grant no. 18-05-01018).
This paper was edited by Philip Woodworth and reviewed by two anonymous referees.
Badyukova, E. N.: Comparative analysis of the structure and genesis of the Northern Caspian Sea islands and the island Ogurchinsky off the coast of Turkmenistan, IGCP 610 Third Plenary Conference and Field Trip “From the Caspian to Mediterranean: Environmental Change and Human Response during the Quaternary”, edited by: Gilbert, A., Yanko-Hombach, V., and Yanina, T., 22–30 September 2015, Astrakhan, Russia, Proceedings, MSU, Moscow, 18–20, 2015.
Baidin, S. S. and Kosarev, A. N. The Caspian Sea: Hydrology and hydrochemistry, Nauka, Moscow, 262 pp., 1986.
Bolgov, M. V., Krasnozhon, G. F., and Lyubushin, A. A.: The Caspian Sea: Extreme hydrological events, edited by: Khublatyan, M. G., Nauka, Moscow, 381 pp., 2007.
Defant, A.: Physical Oceanography (Vol. II), Pergamon Press, Oxford, 598 pp., 1961.
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., Kobrick, M., Paller, M., Rodriguez, E., Roth, L., Seal, D., Shaffer, S., Shimada, J., Umland, J., Werner, M., Oskin, M., Burbank, D., and Alsdorf, D.: The Shuttle Radar Topography Mission, Rev. Geophys., 45, RG2004, https://doi.org/10.1029/2005RG000183, 2007.
German, V. K.: Spectral analysis of water level oscillations in the Azov, Black, and Caspian seas within the range from one cycle over few hours until one cycle over few days, Tr. Gos. Okeanogr. Inst., 103, 52–73, 1970.
Hall, J. K.: Bathymetric compilations of the seas around Israel I: The Caspian and Black Seas, Geological Survey of Israel, Current Research, 13, 105–108, 2002.
Kantha, L. H. and Clayson, C. A.: Numerical models of oceans and oceanic processes, International Geophysics Series, 66, Academic Press, San Diego, 940 pp., 2000.
Kosarev, A. N. and Tsyganov, V. F.: Some statistical characteristics of the water level oscillations in the Caspian Sea, Meteorol. Gidrol., 2, 49–56, 1972.
Levyant, A. S., Rabinovich, A. B., and Rabinovich, B. I.: Calculation of the free-form seiches oscillations in the Caspian Sea, Oceanology, 33, 588–598, 1994.
Malinovsky, N. V.: The tides in the Caspian Sea, Meteorol. Vestn., 5, 116–117, 1926.
Medvedev, I. P.: Tides in the Black Sea: Observations and Numerical Modelling, Pure Appl. Geophys., 175, 1951, https://doi.org/10.1007/s00024-018-1878-x, 2018.
Medvedev, I. P., Rabinovich, A. B., and Kulikov, E. A.: Tidal oscillations in the Baltic Sea, Oceanology, 53, 526–538, https://doi.org/10.1134/S0001437013050123, 2013.
Medvedev, I. P., Rabinovich, A. B., and Kulikov, E. A.: Tides in three enclosed basins: the Baltic, Black and Caspian seas, Front. Mar. Sci., 3, 1–7, https://doi.org/10.3389/fmars.2016.00046, 2016.
Medvedev, I. P., Kulikov, E. A., and Rabinovich, A. B.: Tidal oscillations in the Caspian Sea, Oceanology, 57, 360–375, https://doi.org/10.1134/S0001437017020138, 2017.
Medvedev, I. P., Kulikov, E. A., Fine, I. V., and Kulikov, A. E.: Numerical modelling of sea level oscillations in the Caspian Sea, Russ. Meteorol. Hydro.+, 44, 529–539, https://doi.org/10.3103/S1068373919080041, 2019.
Medvedev, I. P., Kulikov, E. A., and Fine, I. V.: The Caspian Sea tides data, https://doi.org/10.29006/datasets.2020.cst.1, 2020.
Mellor, G. L.: Users guide for a three-dimensional, primitive equation, numerical ocean model. Program in Atmospheric and Oceanic Sciences, Princeton, Princeton University, NJ, 08544-0710, 56 pp., 2004.
Munk, W. H. and Cartwright, D. E.: Tidal spectroscopy and prediction, Philos. T. Roy. Soc. Lond. A, 259, 533–581, https://doi.org/10.1098/rsta.1966.0024, 1966.
Nikiforov, L. G.: On the question of coastal bar formation, Oceanology, 4, 654–658, 1964.
Pugh, D. T. and Woodworth, P. L.: Sea-level science: Understanding tides, surges, tsunamis and mean sea-level changes, Cambridge University Press, Cambridge, ISBN 9781107028197, 408 pp., 2014.
Saha, S., Moorthi, S., Pan, H. L., Wu, X. R., Wang, J. D., Nadiga, S., Tripp, P., Kistler, R., Woollen, J., Behringer, D., Liu, H. X., Stokes, D., Grumbine, R., Gayno, G., Wang, J., Hou, Y. T., Chuang, H. Y., Juang, H. M. H., Sela, J., Iredell, M., Treadon, R., Kleist, D., Van Delst, P., Keyser, D., Derber, J., Ek, M., Meng, J., Wei, H. L., Yang, R. Q., Lord, S., Van den Dool, H., Kumar, A., Wang, W. Q., Long, C., Chelliah, M., Xue, Y., Huang, B. Y., Schemm, J. K., Ebisuzaki, W., Lin, R., Xie, P. P., Chen, M. Y., Zhou, S. T., Higgins, W., Zou, C. Z., Liu, Q. H., Chen, Y., Han, Y., Cucurull, L., Reynolds, R. W., Rutledge, G., and Goldberg, M.: The NCEP Climate Forecast System Reanalysis, B. Am. Meteorol. Soc., 91, 1015–1057, https://doi.org/10.1175/2010BAMS3001.1, 2010.
Spidchenko, A. N.: The tides in the Caspian Sea, Meteorol. Gidrol., 5, 98–100, 1973.
Stammer, D., Ray, R. D., Andersen, O. B., Arbic, B. K., Bosch, W., Carrièe, L., Cheng, Y., Chinn, D. S., Dushaw, B. D., Egbert, G. D., Erofeeva, S. Y., Fok, H. S., Green, J. A. M., Griffiths, S., King, M. A., Lapin, V., Lemoine, F. G., Luthcke, S. B., Lyard, F., Morison, J., Müller, M., Padman, L., Richman, J. G., Shriver, J. F., Shum, C. K., Taguchi, E., and Yi, Y.: Accuracy assessment of global barotropic ocean tide models, Rev. Geophys., 52, 243–282, https://doi.org/10.1002/2014RG000450, 2014.
Tuzhilkin, V. S. and Kosarev, A. N.: Thermohaline structure and general circulation of the Caspian Sea waters, in: The Caspian Sea Environment, The Handbook of Environmental Chemistry, edited by: Kostianoy, A. G. and Kosarev, A. N., vol. 5P, Springer, Berlin, Heidelberg, 33–57, https://doi.org/10.1007/698_5_003, 2005.
Wahr, J.: Body tides on an elliptical, rotating, elastic and oceanless Earth, Geophys. J. Roy. Astr. S., 6, 677–703, https://doi.org/10.1111/j.1365-246X.1981.tb02690.x, 1981.