the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Effects of sea-level rise on tides and sediment dynamics in a Dutch tidal bay
Theo Gerkema
Déborah Idier
Aimée B. A. Slangen
Karline Soetaert
Sea-level rise (SLR) not only increases the threat of coastal flooding, but may also change tidal regimes in estuaries and coastal bays. To investigate such nearshore tidal responses to SLR, a hydrodynamic model of the European Shelf is downscaled to a model of a Dutch coastal bay (the Oosterschelde, i.e., Eastern Scheldt) and forced by SLR scenarios ranging from 0 to 2 m. This way, the effect of SLR on tidal dynamics in the adjacent North Sea is taken into account as well. The model setup does not include meteorological forcing, gravitational circulation, and changes in bottom topography. Our results indicate that SLR up to 2 m induces larger increases in tidal amplitude and stronger nonlinear tidal distortion in the bay compared to the adjacent shelf sea. Under SLR up to 2 m, the bay shifts from a mixed flood- and ebb-dominant state to complete ebb dominance. We also find that tidal asymmetry affects an important component of sediment transport. Considering sand bed-load transport only, the changed tidal asymmetry may lead to enhanced export, with potential implications for shoreline management. In this case study, we find that local impacts of SLR can be highly spatially varying and nonlinear. The model coupling approach applied here is suggested as a useful tool for establishing local SLR projections in estuaries and coastal bays elsewhere. Future studies should include how SLR changes the bed morphology as well as the feedback effect on tides.
Sea-level rise (SLR) poses an increasing flood risk on global shorelines (FitzGerald et al., 2008; Haigh et al., 2014). In addition to the direct increment in water levels (Church et al., 2013; Oppenheimer et al., 2019), SLR induces changes in global and regional tidal regimes (Pelling et al., 2013b; Devlin et al., 2017; Pickering et al., 2017). Understanding these tidal changes is an imperative step towards projecting future water levels and designing shoreline protection works (Katsman et al., 2011; Haasnoot et al., 2019). Shifts in estuarine and coastal tidal regimes including tidal amplitude, residual currents, and tidal asymmetry can potentially modify sediment transport, which further influences shoreline morphology and the accretion (or erosion) of salt marshes and tidal flats (van Goor et al., 2003; Chernetsky et al., 2010; Nnafie et al., 2014). Furthermore, in estuaries and embayments, changes in tidal mixing and currents are expected to have implications for salt intrusion, nutrient transport, primary production, and other ecosystem functions (Nienhuis and Smaal, 1994; Zhang et al., 2010; Winterwerp et al., 2013; de Jonge et al., 2014). Therefore, in order to understand and mitigate the SLR hazards in estuaries and coastal bays, it is of high priority to study the SLR impact on tides.
SLR-induced tidal changes in estuaries and embayments are more complex than in the open ocean and shelf seas (Holleman and Stacey, 2014). Tidal waves propagating in nearshore regions are strongly deformed via factors like shoaling, damping, and reflection (resonance). As these processes respond to SLR to various extents, this triggers spatially heterogeneous modifications in tidal regimes (e.g., Pickering et al., 2012; Carless et al., 2016). Therefore, tidal responses to SLR vary among and within systems (Holleman and Stacey, 2014; Pelling and Green, 2014). For example, with SLR, the tidal amplitude may increase due to reduced friction (Arns et al., 2015; Idier et al., 2017) or decrease as a consequence of enhanced dissipation in the newly inundated areas (Pelling et al., 2013a; Ross et al., 2017). Overtides and tidal asymmetry can also be modulated distinctly among estuaries, with ramifications for residual sediment transport and morphodynamic development (Hoitink et al., 2003; van der Wegen, 2013; Gräwe et al., 2014; Dijkstra et al., 2019a). In estuaries and tidal bays, the direction and extent of tidal asymmetry depend on the tidal amplitude (a) to basin depth (h) ratio, a∕h, as well as the volume ratio of intertidal regions (Vs) to channels (Vc), Vs∕Vc (Friedrichs and Aubrey, 1988). Large a∕h and Vs∕Vc ratios point to high tendency of flood and ebb dominance, respectively (Friedrichs and Aubrey, 1988). While the Vs∕Vc ratio decreases with SLR, how a∕h is influenced by SLR is less straightforward, as it depends on the specifics of the basin in question (Brown and Davies, 2010). Thus, given the various responses in different types of basins, tidal impacts of SLR should be assessed on a system- or site-specific basis.
Changes in tidal amplitude in coastal oceans and estuaries can be caused by anthropogenic activities (e.g., dredging, land reclamation) and climate change (Haigh et al., 2019; Talke and Jay, 2020). The impacts of SLR on estuarine and riverine tides are analogous to those of channel deepening owing to dredging and sand mining, as both are associated with increased water depth (Talke and Jay, 2020). Winterwerp and Wang (2013) found in a theoretical study that narrowing and deepening of small convergent estuaries tends to increase tidal amplitude and flood dominance, resulting in a hyper-turbid state. Deepening-induced stronger tidal amplitude is reported in the Ems (de Jonge et al., 2014), Hudson (Ralston et al., 2019), and Loire rivers (Winterwerp et al., 2013), as well as the Cape Fear River estuary (Familkhalili and Talke, 2016), especially in the upper reach. Tidal responses to deepening also show intra- and inter-system variability due to the various deepening extents and characteristics of estuaries (Talke and Jay, 2020). For instance, the partially dredged Newark Bay exhibits spatially variable changes in tidal range (Chant et al., 2018). While retrospective analyses of deepening-induced tidal alterations have implications for potential shifts under SLR circumstances, it is noteworthy that they are not the same. Dredging activities are mainly conducted at tidal channels and are spatially nonuniform, whereas SLR occurs throughout the estuary, as well as in the adjacent coastal seas (Ralston et al., 2019).
Although challenging, tidal changes due to SLR have been modeled in both idealized and realistic estuaries and bays (e.g., Hong and Shen, 2012; Pelling et al., 2013b; Holleman and Stacey, 2014; Ensing et al., 2015; Passeri et al., 2016; Du et al., 2018). Generally, studies with idealized (simplified) basin shapes cannot fully address the spatially nonuniform shoaling, reflection, and damping in realistic systems. Furthermore, in many modeling studies, SLR is prescribed by simply increasing the surface elevation at the open boundary, without taking into account the tidal changes in the adjacent shelf sea itself, which would radiate into the estuaries and bays (e.g., Hong and Shen, 2012; Holleman and Stacey, 2014; Ross et al., 2017). In fact, before entering estuaries, tidal waves on the shelf can be significantly modified in amplitude and phase or distorted (Jay et al., 2010; Idier et al., 2017). Chernetsky et al. (2010) found that the externally generated overtides play a key role in the sediment dynamics within an estuary. Additionally, tidal changes in estuaries and shelf seas may exert a strong influence on tides in the ocean (e.g., Ray, 2006; Arbic and Garrett, 2010). This underlines the necessity of coupling the coastal and shelf processes with the dynamics of landlocked water bodies for SLR assessments (e,g., Zhao et al., 2014; Rasquin et al., 2019).
Here, we present a case study with regional SLR projections driving a hydrodynamic model of the European Shelf, which was then downscaled for the Oosterschelde (English name: Eastern Scheldt), a Dutch tidal bay adjacent to the North Sea (Fig. 1). We investigate the SLR impacts on the local tidal dynamics and the implications for residual sediment transport. This study also explores the necessity of the model coupling method when predicting SLR influences in other estuaries and coastal bays.
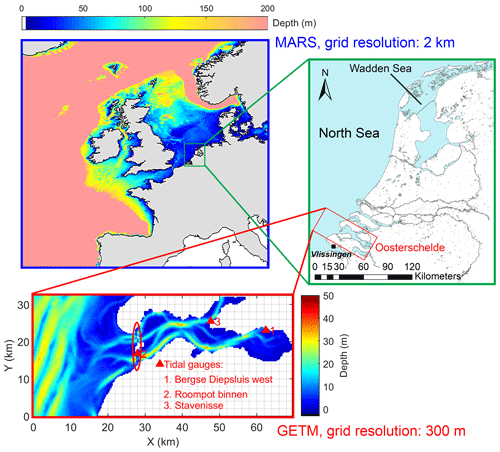
Figure 1The study area and domains of the two hydrodynamic models representing the European Shelf (blue) and Oosterschelde (red). The green box shows the locations of the Oosterschelde and local SLR projection, Vlissingen, in the zoomed-in map of the Netherlands. In the Oosterschelde domain, tide gauges used for model calibration and the location of the storm surge barrier are marked with triangles and an ellipse, respectively; white areas are land segments protected by dikes where flooding is not allowed.
The Oosterschelde is a well-mixed tidal bay on the southwestern coast of the Netherlands (Fig. 1). Because of the limited freshwater input, the semidiurnal-dominant tides control the water renewal and material transport in the Oosterschelde (Jiang et al., 2019a). A storm surge barrier (hereafter referred to as “barrier”; Fig. 1) constructed at its mouth in the late 1980s reduced the tidal prism and amplitude by ∼30 % and 13 %, respectively. As a result, the tidal flat and salt marsh areas and landward supply of sediments, nutrients, seston, and chlorophyll sharply declined, and the residence time was doubled (Nienhuis and Smaal, 1994). Due to a decreased sediment source and reduced tidal range, erosion of tidal flats is ongoing, disturbing ecosystem services in the bay (Vroon, 1994). Since the construction of the barrier, tides have not been substantially changed by the changing bed morphology of the basin (de Pater, 2012).
In surrounding systems such as the Western Scheldt estuary and Rotterdam waterway, south and north to the Oosterschelde, respectively, tides and sediment dynamics have been changing over the last century as a result of sand mining, dredging, and modifications of shorelines and navigation channels (Winterwerp et al., 2013; van Rijn et al., 2018; Cox et al., 2019; Dijkstra et al., 2019a). The tidal range in the southern North Sea has increased since the 1950s, partially due to the engineering works on the Dutch Delta (Hollebrandse, 2005).
In the future, SLR at the Dutch coast may exceed 1 m between 2000 and 2100 under a high greenhouse gas emission scenario (Vermeersen et al., 2018). Shelf-study models indicate that, with SLR, the M2 amphidromic point in the southern North Sea moves northeastwards, further away from the Dutch Delta but closer to the Wadden Sea, inducing a decreased (increased) M2 amplitude on the northern (southern) Dutch coast (Pickering et al., 2012; Idier et al., 2017). The overall tidal amplitude (mostly semidiurnal components) adjacent to the Dutch Delta is projected to increase, mainly due to reduced friction and amphidrome movement (Pickering et al., 2012; Pelling et al., 2013a; Idier et al., 2017). As a result of the increased water depths on the European shelf, tidal phase speed is increased, leading to the earlier arrival of semidiurnal tidal waves, i.e., reduced semidiurnal phases, in the southern North Sea (Idier et al., 2017). The SLR-induced increased tidal amplitude may reverse some of the above post-barrier declining trends, highlighting the need to explore the local tidal responses to SLR in the Oosterschelde.
We used the hydrodynamic model MARS (Model for Applications at Regional Scale; Lazure and Dumas, 2008) to model tides on the European Shelf at a horizontal resolution of 2 km. Given that the Oosterschelde and the entire Dutch Delta were represented in the MARS domain with a relatively low spatial resolution, in a downscaling setup, GETM (General Estuarine Transport Model; https://getm.eu/, last access: 2 March 2020) was used to model tides in the Oosterschelde at a resolution of 300 m (Fig. 1). Our study applies a one-way nesting technique that accounts for the communication from the larger (MARS) to smaller (GETM) domain, but not the other way. The description and setup of these two models were detailed by Idier et al. (2017) and Jiang et al. (2019a), respectively. This section therefore focuses on the model coupling setup, SLR scenarios, and model calibration.
MARS was forced with all tidal components from the global tide model FES2004 (Lyard et al., 2006), i.e., Mf, Mm, Msqm, Mtm, O1, P1, Q1, K1, M2, K2, 2N2, N2, S2, and M4. The MARS domain (Fig. 1) covers the entire northwest European continental shelf and extends to deep waters (>200 m) so that the SLR-induced changes in tidal components at its open boundary are minimal. The year 2009 was used as the baseline scenario, and the observed water elevation and tidal components from 16 tide gauges were well reproduced by MARS for that year (Idier et al., 2017).
The SLR scenarios were implemented in MARS by uniformly increasing the open-boundary water level in the baseline scenario. Using the water level data from a regional SLR projection model (Slangen et al., 2014), Idier et al. (2017) also tested a scenario with nonuniform open-boundary SLR and found insignificant differences of tides from the uniform scenarios in the southern North Sea. Thus, only the MARS results with uniform SLR scenarios were used for downscaling to the Oosterschelde model. The SLR scenarios used for the MARS model are 0.25, 0.5, 0.75, 1.0, 1.5, and 2.0 m. The regional projection at Vlissingen by Slangen et al. (2014) was used to estimate the SLR timescale in the Oosterschelde, which is included in some figures as an indication (the SLR rate itself does not feature in the model runs). In the MARS domain, most low-lying land within 2 m of height above the present sea level is located on the eastern shore of the North Sea, i.e., Belgium, the Netherlands, Germany, and Denmark (http://flood.firetree.net/, last access: 2 March 2020), where the coastlines are well protected from flooding (Pelling and Green, 2014). Hence, the SLR scenarios were conducted without flooding of these shorelines in both MARS and GETM. Given the uncertainties of bottom topography in the future, a constant bathymetry was used in the baseline and SLR scenarios. Atmospheric forcing and baroclinic effects were not included in the model setup.
GETM was used to downscale MARS to the Oosterschelde in a one-way coupling and 2D barotropic mode. The barrier consists of two artificial islands and three tidal openings (Fig. 1), and each opening is facilitated by concrete pillars and steel gates that can be closed under severely stormy conditions. While our model resolution is incapable of representing each pillar (<4 m wide), the cross-sectional area of pillars, ∼8.2 % of the overall area, was compensated for by reducing the depth by the same percentage at the “barrier” cells in the model. Given the uncertainties in future bed morphology and bottom roughness, we applied a spatially constant bottom roughness length scale of 1.7 mm in the baseline and all SLR scenarios as used in the Wadden Sea (Duran-Matute et al., 2014). Wetting and drying of tidal flats in the Oosterschelde was solved in GETM, while the shoreline (white areas in the GETM domain; Fig. 1) stayed unflooded. The Flather open boundary (Flather, 1988) was applied in GETM, in which the gravity-wave radiation condition requires prescribing both water elevation and current velocity as boundary forcing. In the baseline and SLR scenarios, these two variables in the vicinity of the GETM open boundary (Fig. 1) were extracted from MARS output every 15 min and linearly interpolated to each GETM open-boundary node (255 nodes total; Jiang et al., 2019a). Every scenario was run for 1 year (2009), and the time series of modeled tidal elevation and currents were decomposed with the T_TIDE toolbox (Pawlowicz et al., 2002) to extract the major components for all grid cells excluding the tidal flats.
Observational water elevation data at three stations in the east, middle, and west of the Oosterschelde (Fig. 1) were obtained from the Dutch government agency Rijkswaterstaat website (https://www.rijkswaterstaat.nl/water, last access: 2 March 2020) and compared with the sea surface height in the GETM baseline output. Note that the observed water elevation is influenced by tides as well as winds and gravitational circulation, while the model is only tide-forced. The correlation coefficients, standard deviations, and root mean square differences (RMSDs) between modeled and observed water level were calculated to plot a Taylor diagram (Taylor, 2001). Harmonic analyses were conducted on both observed and simulated water elevation to compare the magnitude and phase of the resultant M2 and M4 components. The absolute error (simulation–observation) and relative error (absolute error divided by observation) were used to denote the fit for the phase and magnitude, respectively (Fig. 2).
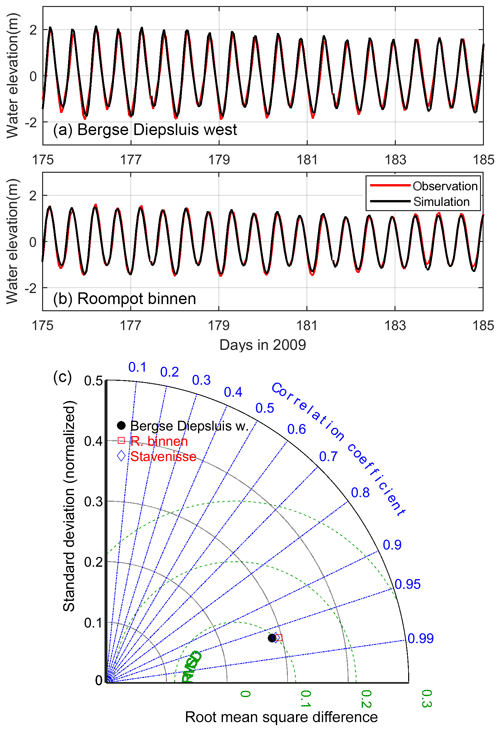
Figure 2(a, b) Time series of modeled and observed water elevation and (c) the Taylor diagram of the water elevation comparison. See Fig. 1 for the locations of data sites.
Tidal asymmetry was estimated using the phase difference between the M2 and M4 currents following Friedrichs and Aubrey (1988): a positive, zero, and negative value of indicates flood dominance, symmetric tide, and ebb dominance, respectively, where and are the phases of M2 and M4 current velocity, respectively. Changing tidal asymmetry may exert an alteration in the sediment budget of a system. Sediment transport is a complex function of sediment properties, tidal dynamics, gravitational circulation, and other processes (e.g., van der Wegen et al., 2011; Dijkstra et al., 2017; Schulz and Gerkema, 2018) and would require solving the basin-wide dynamic sediment transport of all grain sizes and geomorphological changes in the current and future conditions. Here we aim to gain insight into the potential implications for sediment transport due to changes in tidal asymmetry alone, i.e., by focusing on a component of sediment transport. Specifically, we used the analytical quantity Q (kg m−1 s−1, Eq. 1) proposed by Gräwe et al. (2014), which applies to systems with relatively weak stratification and estuarine circulation, such as the Oosterschelde (Burchard et al., 2013).
In Eq. (1), α is the sediment erosion parameter (kg s m−4), κv is the vertical diffusion coefficient (m2 s−1), ws is the settling velocity (m s−1), and UM2 and UM4 are the magnitude of the M2 and M4 current velocity (m s−1), respectively. Because most of the post-barrier sediment in the Oosterschelde is sandy (ten Brinke et al., 1994), we focus on a typical kind of sand with values of α (0.001) and ws (0.001) as suggested by Burchard et al. (2013) and Gräwe et al. (2014) for weakly stratified estuaries and the North Sea. Q represents sand bed-load transport as it assumes a negligible settling time lag between the local suspended sediment concentration and currents. U, κv, and ϕ were calculated from different SLR scenarios. The analysis based on Q saves substantial computational time compared to applying a sophisticated sediment transport model.
4.1 The baseline scenario
Our modeled water elevation in the baseline scenario (SLR=0) matches well with the observed water level at tide gauges, with overall correlation coefficients >0.95 and RMSDs (dimensionless) <0.1 (Fig. 2). For example, Fig. 2a and b show good agreement between simulated and observed water elevation during days 175–185, a period with relatively weak winds (this period was chosen as the coupled models were run without atmospheric forcing). In addition to the water level, the model captures the observed magnitude and phase of M2 and its major overtide M4 with relatively small errors (Fig. 3a). The errors of observed and modeled M2–M4 phase difference (2ϕM2−ϕM4) are −6.2, 13.5, and 21.3∘ at Roompot binnen, Stavenisse, and Bergse Diepsluis west, respectively (Fig. 3b), which may result from the meteorological forcing and gravitational circulation that is lacking in the model. The model overestimates the extent of flood and ebb dominance, but the direction of tidal asymmetry agrees with the observation (Fig. 3b). The spatial asymmetry of vertical tides, i.e., flood dominance in the west and ebb dominance in the middle and east, also matches the previous results with the 2008 observational data (de Pater, 2012).
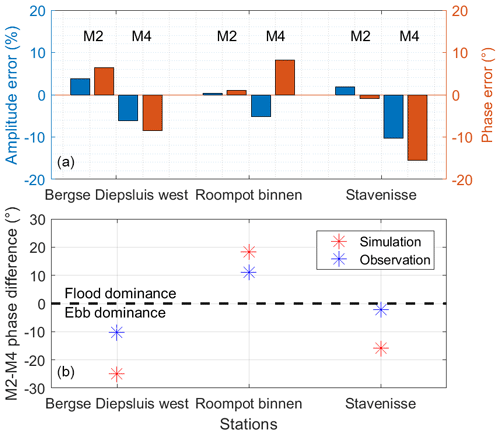
Figure 3The simulated (a) M2 and M4 amplitude and phase errors and (b) M2–M4 phase difference compared to observations. Note that these M2 and M4 tides are calculated based on vertical tides rather than horizontal tides, i.e., different from those in Figs. 6 and 7. Tidal asymmetry is defined based on Friedrichs and Aubrey (1988). See Fig. 1 for the locations of data sites.
The tidal range (TR) increases from 2.5 to 3.4 m from the mouth to head (Fig. 4a). As the dominant component in the Oosterschelde, the M2 magnitude captures most of the TR spatial pattern, and it takes ∼30 min (phase difference ∼15∘) for the semidiurnal tidal wave to propagate from the western to eastern side (Fig. 5c). With the basin length L=40.8 km, the average M2 phase speed of the basin (cM2) is approximately 22.7 m s−1. This phase speed is much faster than the shallow-water wave speed in inviscid and frictionless systems, m s−1, where h is the average depth of the bay, 7.0 m. Based on our field measurements and model calculation, the phase difference between the horizontal and vertical tides is close to 90∘, indicating that the tidal waves in the basin are nearly standing waves. The landward-increasing tidal amplitude, the amplified phase speed compared to c0, and the properties of nearly standing waves are all important features of a convergent system rather than a frictional damping system (Hunt, 1964; Jay, 1991; Friedrichs and Aubrey, 1994; Lanzoni and Seminara, 1998; Savenije and Veling, 2005; van Rijn, 2011). The convergence in cross-sectional area is a result of narrowing in the west and shoaling (increased areas of tidal flats) in the east (Figs. 1 and 6). The sharply reduced water depth caused by the barrier at the mouth (Fig. 1) significantly weakens the tidal amplitude and delays the propagation of tidal waves (Figs. 4 and 5). This discontinuity in the tidal amplitude and phase between the North Sea and Oosterschelde is consistent with post-barrier observations (Vroon, 1994).
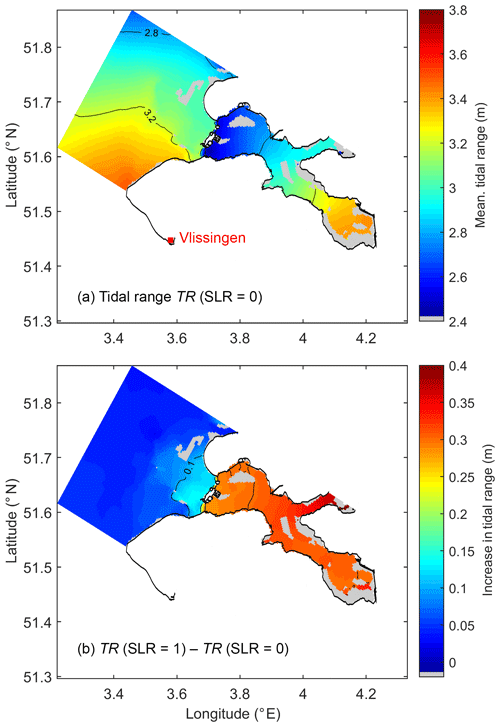
Figure 4(a) Tidal range in the baseline scenario and (b) the difference in tidal range between the 1 m SLR and baseline scenarios. Tidal flats are shown in grey. Tidal range is calculated as the annual average of the difference between high and low water in every tidal cycle.
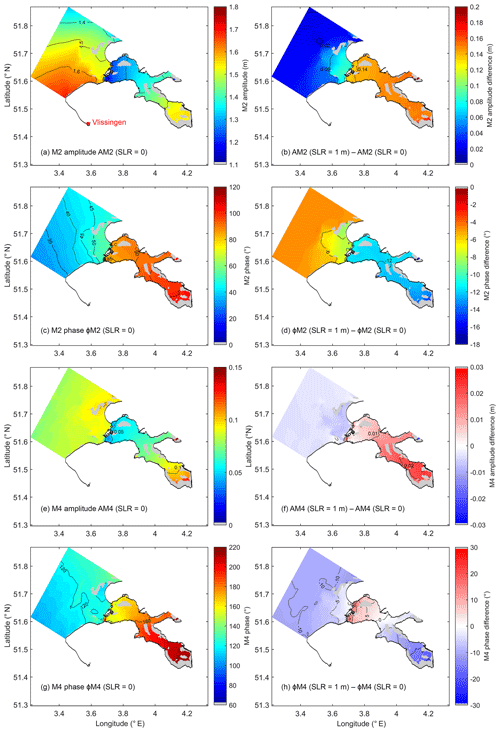
Figure 5The M2 (a) amplitude and (c) phase and M4 (e) amplitude and (g) phase in the baseline scenario and (b, d, f, h) the difference in these variables between the 1 m SLR and baseline scenarios. Tidal flats are shown in grey.
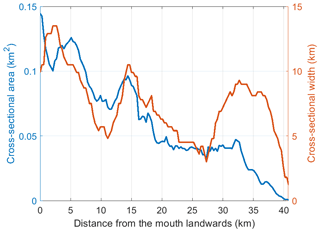
Figure 6The cross-sectional area and width of the Oosterschelde from the mouth to its eastern end. The northern branch (Fig. 1) is excluded from the calculation because of a different orientation of channels.
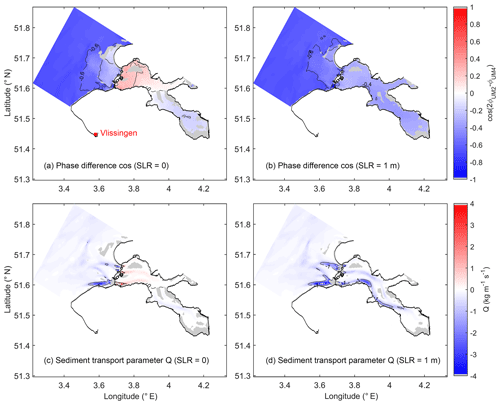
Figure 7a shows the M2–M4 phase difference of the horizontal tides (current velocity) in the baseline scenario, which is consistent with that calculated from the vertical tides. That is, inside the bay, the western and eastern parts show flood and ebb dominance, respectively (Fig. 7a). The barrier marks a boundary of changed tidal asymmetry, separating the ebb and flood dominance outside and inside, respectively (Fig. 7a).
4.2 SLR effects on the tidal amplitude and phase
In the absence of sediment deposition and erosion, the tidal flats will be gradually inundated by the increasing sea level at an accelerated pace (Fig. 8a). With SLR, TR increases within the Oosterschelde, especially at the landward ends (e.g., Fig. 4b). The average TR over the entire bay increases nearly proportionally to SLR according to the linear regression (r2>0.995), all in meters, indicating an 11.5 % increase in TR per meter SLR (Fig. 8a). Our study considers SLR up to 2 m, in which range the above relationship and other findings in Sect. 4.2 and 4.3 apply. It should be noted that r2 only denotes the goodness of fit of the linear model. With the assumptions made in the SLR scenarios and simplifications of our 2D barotropic model, the uncertainty level of the regression is at least 10 % given the 0.1 RMSDs between the modeled and observed water elevation (Fig. 2c). In the pre-barrier period (1900–1980), a 25 cm SLR increased the tidal amplitude by 3 %–4 % in the Oosterschelde (Vroon, 1994), which is comparable to our estimated rate (11.5 % per meter SLR). This rate is much faster than that in the adjacent North Sea in the GETM domain, where (r2>0.995, Fig. 8a), as well as the entire southern North Sea (Idier et al., 2017). In the 1980s, TR declined by ∼0.35 m due to the construction of the barrier so that, based on our estimation, the pre-barrier magnitude will be restored at around 1 m SLR, which may occur by the end of the 21st century (Fig. 8a).
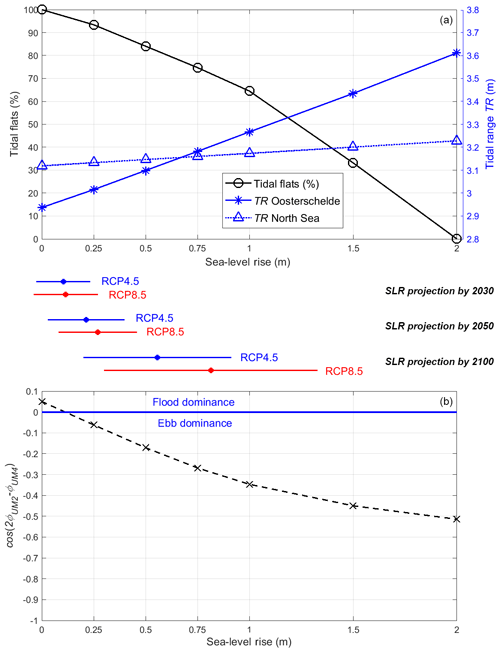
Figure 8(a) Variations of the basin-average tidal flat percentage (defined as 100 % in the baseline scenario) and average tidal range of the Oosterschelde and North Sea in the baseline and SLR scenarios; (b), same as (a), but for the cosine of M2–M4 velocity phase difference averaged over the Oosterschelde. The scales between the two panels are the local SLR projections (between the 5 % and 95 % confidence levels) in emission scenarios RCP4.5 and RCP8.5 in future decades, and the dots on each scale denote projection medians.
The increase in M2, S2, and M4 amplitudes in the bay is also proportional to SLR, with a slope of 0.157, 0.056, and 0.029 m m−1 SLR (r2>0.995). These increasing magnitudes per meter SLR account for 11.3 %, 15.7 %, and 40.4 % of the M2, S2, and M4 magnitude in the baseline scenario, respectively. The spatial patterns of the semidiurnal components M2 and S2 are similar to that of the overall TR, and accordingly they are more sensitive to SLR inside the bay compared to outside (e.g., Fig. 5b). In contrast, under SLR the M4 amplitude decreases outside, while it increases inside the Oosterschelde (Fig. 5f). We conducted a hypothetical model run, in which tides in the 1 m SLR scenario of the MARS model were prescribed to the GETM open boundary, while the sea level stayed the same as the baseline run. Results in this run indicate that the M4 amplitude decreases out of the bay similarly as shown in Fig. 5f and hardly changes in the bay. Thus, the decrease in M4 amplitude out of the bay results mainly from the MARS domain, whereas the M4 amplitude in the basin is largely modulated by the changing sea level. Compared to the baseline scenario, the M4 amplitude in the bay increases (40.4 % per meter SLR) much faster than TR and the main semidiurnal components.
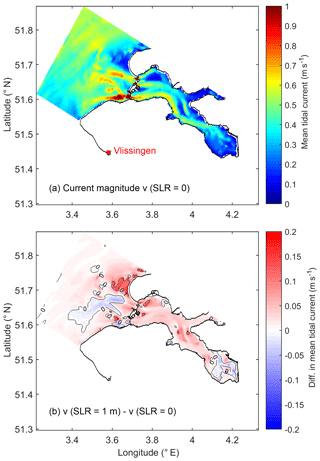
As a result of the movement of the amphidromic point and reduced friction (Idier et al., 2017), the M2 tide in the southern North Sea arrives earlier under SLR (Fig. 5d). The convergent property of the Oosterschelde (Sect. 4.1) amplifies the vertical and horizontal M2 tide (Fig. 5b and d). Consequently, the phases of semidiurnal components decrease with SLR, with a larger change in the bay than in the coastal sea and at the landward ends than at the seaward ends (e.g., Fig. 5d). This can explain the accelerated tidal currents under SLR (Fig. 9). In contrast, the M4 phase varies in a nonuniform and nonlinear way, implying strong modifications of shallow-water tides under SLR (Fig. 5h).
4.3 SLR-induced shifts in tidal asymmetry and implications for sediment transport
The different responses of M2 and M4 under SLR conditions change the tidal asymmetry in the Oosterschelde. The entire bay shifts from a mixed ebb and flood dominance (Fig. 7a) to an increasingly ebb-dominant state (Fig. 7b). The switch of the entire bay already occurs at SLR below 0.25 m, as indicated by the M2–M4 phase difference (Fig. 8b). In the scenario with 1 m SLR, the flood-dominant western part becomes ebb-dominant, while the ebb dominance in the eastern part is enhanced; in contrast, the M2–M4 phase difference in the adjacent North Sea is relatively insensitive to SLR (Fig. 7b).
The quantity Q, an indicator of sand bed-load transport, is used to estimate the combined effects of tidal current velocity and asymmetry. With both tidal currents (Fig. 9b) and ebb dominance (Fig. 7b) strengthened by SLR, the absolute value of Q is amplified, and the direction becomes completely seaward (Fig. 7d). The increasing seaward Q under SLR (Fig. 7d) is mainly through channels where tidal currents are strong (Figs. 7d and 9a). Tidal asymmetry is one important mechanism of sediment transport among others (density-driven transport, lateral transport, etc.). While Q in this study cannot be used for quantifying the full sediment budget of the basin, it sheds light on possible transitions in sediment transport directions. In the pre-barrier period, the sand erosion and sedimentation of tidal flats were in equilibrium in the Oosterschelde (ten Brinke et al., 1994). The barrier acts as an obstacle to sand import, while the reduced tidal currents cannot resuspend and supply sufficient sand to the eroded tidal flats, creating a sand deficit for tidal flats (Eelkema et al., 2012). Our results imply that despite the fact that SLR can restore the pre-barrier TR (Sect. 4.2), the increased ebb dominance may have an adverse impact on sand import. Note, however, that the fate of tidal flats remains uncertain given the unaddressed mud transport in this study and many details such as the shape of tidal flats and wave action (van der Wegen et al., 2017).
This case study shows how future SLR may change the tidal regime and residual sediment transport in a tidal bay. Understanding tidal responses to SLR is fundamental to anticipating any ecosystem shifts and adjusting management strategies in global estuaries and bays. For instance, a 1 m SLR can increase the mean high water level in the Oosterschelde by 0.16 m, about half of the increase in tidal range (Fig. 8a). However, in this scenario, the increase in high water at spring tides can be up to 30 cm, which implies that at least an extra 30 cm needs to be accounted for in dike construction in addition to the 1 m SLR, as similarly reported for other coastal systems (Arns et al., 2015; Devlin et al., 2017). As TR increases under SLR, the turnover time, an indicator of water renewal efficiency, is significantly shortened in most parts of the basin (Fig. 10). This will put the system under a greater influence of the North Sea, likely increasing the import of nutrients and organic matter and affecting the carrying capacity of shellfish culture (Jiang et al., 2019a). In many other nearshore systems, tidal changes as a result of SLR were also found to alter the ecosystem functions (Bhuiyan and Dutta, 2012; Hong and Shen, 2012).
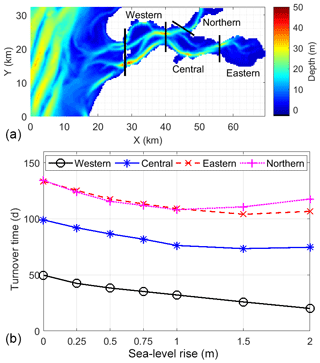
Figure 10(a) Division of four compartments in the Eastern Scheldt and (b) the turnover time of each compartment in the baseline and SLR scenarios. The calculation of turnover time is detailed in Jiang et al. (2020).
One intriguing finding in our study is a much stronger response of tidal range to SLR in the bay compared to the adjacent coastal sea (Fig. 8a). This is not a consequence of enhanced resonance. In strongly dissipative basins, SLR reduces the phase speed and the ratio of basin length to wavelength and increases the resonance-induced amplification of tidal magnitude (Talke and Jay, 2020). In our study, if the classical phase speed c0 is applied, the quarter-wavelength resonance period of our system (; see, e.g., Gerkema, 2019) in the baseline scenario is 5.5 h. As a convergent basin, when the average M2 phase speed cM2=22.7 m s−1 (Sect. 4.1) is used, the quarter-wavelength resonance period should be 2.0 h in the Oosterschelde. The Helmholtz resonance, which assumes a uniform tidal phase in a tidal bay, does not apply to the Oosterschelde because of the along-channel semidiurnal phase difference (∼15∘, 30 min; Fig. 5c). Moreover, the Helmholtz resonance period (, where A is the basin surface area and Lb, B, and H are the length, width, and depth of the channel connecting the bay and North Sea; e.g., Sutherland et al., 2005; Gerkema, 2019) for the Oosterschelde is no longer than 2.4 h. Both T and TH are much shorter than the semidiurnal tidal period. With h, cM2, and H increased with SLR and L,Lb, and B unchanged, T and TH will decrease and shift further away from semidiurnal resonance. With the resonance impacts ruled out, the increased TR due to SLR in the Oosterschelde can result from reduced friction and the amplifying nature of a convergent basin. In a dissipative basin, SLR and channel deepening can reduce the bottom friction and increase tidal amplitude (e.g., Winterwerp et al., 2013; de Jonge et al., 2014). With the declining friction, the system can even shift from a damping into amplifying basin, such as the Hudson River (Ralston et al., 2019). In a convergent basin, the responses of tidal amplitude to SLR is always stronger at the landward than the seaward ends, as found in our study (Fig. 5b and f) and by Ensing et al. (2015). Changing inlet cross-sectional area due to SLR, usually by inlet widening, can also alter tides in the bay due to changed choking effect (Passieri et al., 2016; Talke and Jay, 2020). In our case, the bathymetry and anthropogenic islands at the storm surge barrier are resistant to flooding so that the choking effect is not modified by SLR.
Another major finding of this study is the SLR-induced changes in tidal asymmetry with potential effects on sediment transport. Tidal distortion and asymmetry result from interactions between basin geometry and shallow-water tidal waves (Speer and Aubrey, 1985). Shallow waters with a high a∕h ratio are usually flood-dominant because tides propagate faster during high water than low water, while an extensive intertidal area flanking deep channels can slow down flood propagation and generate ebb dominance (Friedrichs and Aubrey, 1988). With SLR, the water depth increases, and tidal flat area diminishes. These two processes render the system less flood-dominant and less ebb-dominant, respectively. The shift of tidal asymmetry depends on these two competing effects (Friedrichs et al., 1990). The comparable magnitude of these two effects can result in the relative insensitivity of tidal asymmetry to SLR in the Ria de Aveiro lagoon (Lopes and Dias, 2015) and to deepening in the Western Scheldt (Winterwerp et al., 2013). The SLR-induced shift to ebb dominance in the Oosterschelde implies a stronger reduction in a∕h than Vs∕Vc. In a strongly convergent and less strongly dissipative basin, the overtide magnitude increases landward (Lanzoni and Seminara, 1998), as in the Oosterschelde (Fig. 5e). When the relative strength of convergence to dissipation increases, such systems will become more distorted (i.e., M4 is amplified more than M2) and ebb-dominant (Lanzoni and Seminara, 1998). Under SLR, the basin geometry in our study (Fig. 6) does not change, while friction is reduced due to increased water depth; i.e., friction becomes weaker relative to convergence. The SLR-induced phenomena that M4 increases faster than M2 (Sect. 4.2) and that the ebb dominance is enhanced (Fig. 7b) are consistent with findings by Lanzoni and Seminara (1998). In contrast, the friction-dominated Ems estuary acquires a stronger flood-dominant signal with increasing water level (Chernetsky et al., 2010; Winterwerp et al., 2013). Both suspended and bed-load sediment transport are strongly associated with tidal asymmetry, especially in weakly stratified estuaries, and are important to the long-term basin geomorphology (van Maren et al., 2004; Burchard et al., 2013). For example, with the deepening of the Ems estuary, the increased flood dominance promotes the import of suspended sediment, causing a hyper-turbid state in the estuary (Talke et al., 2009; Winterwerp and Wang, 2013; Dijkstra et al., 2019b). In our study, the shift to ebb dominance changes an important component of sediment transport Q (Fig. 7d), which may be detrimental to shoreline protection and salt marsh accretion.
Although our results are not generic to global estuaries and bays, this study shows the complicated interaction between basin geometry and tides and pinpoints the urgency of understanding estuarine tidal responses under changing SLR conditions. To this end, our case study highlights the following aspects to be fully considered in future studies.
Firstly, tidal responses to SLR can vary from system to system, and comparative studies (e.g., Passeri et al., 2016) are needed. Because of the spatially varying coastline and bathymetry, shallow-water tides react to friction, reflection, and cross-sectional convergence to different extents among and within systems under SLR (e.g., Fig. 8a; Carless et al., 2016; Idier et al., 2017). Thus, compared to shelf-sea models, estuarine models with refined spatial resolution are required to capture the detailed features of bathymetry and coastlines and hence nearshore tidal distortion.
Secondly, in addition to water height, SLR-induced tidal variations in the shelf seas have significant impacts on estuarine and embayment dynamics. Tides in shelf seas exhibit nonlinear and nonuniform responses to SLR (Idier et al., 2017; Pickering et al., 2012), and these effects may penetrate or amplify in estuaries and bays (Ensing et al., 2015). Nevertheless, many previous studies on SLR effects on estuaries simply increased the water level, neglecting changes in the tidal characteristics at their coastal boundary (e.g., Hong and Shen, 2012; Holleman and Stacey, 2014). Based on our results of a scenario increasing the open-boundary water height only, such a simplification overestimates (underestimates) the TR in the Oosterschelde (North Sea) by 9 cm (4 cm) for 1 m SLR and completely misses the reduction of tidal phases. Without variations in externally generated M4 tides, the calculation of estuarine tidal asymmetry and sediment transport can produce different results (Chernetsky et al., 2010). Therefore, given the relatively coarse resolution of shelf-sea models in estuaries and the inability of estuarine models to resolve the shelf-sea tidal variations due to SLR, model coupling is essential in examining nearshore SLR impacts. In addition, the tidal changes in estuaries and embayments may exert an influence on tides in the shelf seas (Ray, 2006). Note, however, that the feedback from the Oosterschelde to the North Sea is not simulated in our model coupling and would make an interesting future study.
Thirdly, nearshore studies should be combined with regional SLR projections to steer efficient shoreline management strategies. Despite large uncertainties associated with emission scenarios and sea-level contributions (Slangen et al., 2014), regional SLR projections provide specific timelines for tidal changes and set the time window for required management actions in the coming decades. For example, the shift to ebb dominance will likely occur before 2050, while nourishment of intertidal flats will be continuously needed well beyond 2100 (Fig. 8). Shoreline defense against SLR ranges from hard measures that prevent flooding, such as levees and dikes, as in the Netherlands, to soft measures that allow flooding, such as using marshes and newly inundated areas for dissipating tidal waves, for instance in parts of the Chesapeake Bay (Lee et al., 2017) and San Francisco Bay (Holleman and Stacey, 2014). Including hard or soft coastal defense measures in numerical models can significantly affect the sensitivity of tides to SLR (Ensing et al., 2015; Idier et al., 2017; Ross et al., 2017; Feng et al., 2019). In our model setup, intertidal flats around channels were allowed to drown, while the shorelines with dikes were not (Fig. 1) so that the reduction of cross-sectional area in Fig. 6 does not vary much with SLR. In a convergent system as the Oosterschelde, if shoreline flooding is fully or partially allowed, the spatial convergence may change accordingly. Clearly, the projections resulting from our study might greatly change if the actual shoreline defense were to be implemented differently.
It should be noted that our coupled model does not account for winds and the gravitational circulation. According to recent studies, wind climate can significantly contribute to the long-term variability of regional water elevation (Arns et al., 2015; Gerkema and Duran-Matute, 2017). Density-driven flow can also dominate local transport processes (Geyer and MacCready, 2014; Burchard et al., 2018; Schulz and Gerkema, 2018). Another limitation of the study is not considering changes in bed morphology, which may, in turn, have an influence on basin properties (e.g., bottom roughness, cross-sectional convergence), tides, and the fate of tidal flats (Ganju and Schoellhamer, 2010). Field measurements on the effect of bed morphology on bottom roughness and shear stress (e.g., Cheng et al., 1999; Prandle, 2004) will improve the simulation and projection of tidal currents. While tides in the Oosterschelde were not strongly affected by bathymetric changes in the past decades (de Pater, 2012), it would be interesting to investigate the interaction between SLR and basin morphology by implementing a geomorphology component into our model. With such a component, sediment of all grain sizes can be considered and the influence of bed morphology changes on tides can be addressed. However, projecting the geomorphic adaptation under SLR is challenging given the uncertainties in the future meteorological forcing, marine and fluvial sediment sources, and grain size distribution (Ganju and Schoellhamer, 2010; Elmilady et al., 2019). The SLR rate, as well as its pace relative to the basin morphodynamic response, is also critical to the morphological development (Zhou et al., 2013; Lodder et al., 2019). In addition to the natural development of bed morphology, future anthropogenic activities such as dredging may change the regional bathymetry in estuaries and bays (Ralston et al., 2019). Despite the similarities to SLR processes, dredging activities involve deepening of only the tidal channel and likely changes in bottom slopes, and therefore the tidal responses can differ (Ensing et al., 2015).
This study applies a one-way model nesting approach to investigate how SLR affects tidal range and asymmetry in the Oosterschelde, a coastal bay located in the southwest Dutch Delta. The local model domain comprising the Oosterschelde and part of the adjacent North Sea imports water elevation from a European Shelf model (Idier et al., 2017) in the year 2009 and under SLR ranging from 0 to 2 m, which may possibly occur in this and the next century. There is no feedback of changes from the Oosterschelde model to the shelf model. Neither model accounts for the meteorological forcing, baroclinic effects, and changes in bottom topography.
Under these assumptions, the “static” (no erosion and accretion) tidal flats are submerged under up to 2 m SLR. As a convergent basin, the Oosterschelde exhibits greater increases in the tidal range and amplitude of semidiurnal and quaterdiurnal components than the North Sea under SLR up to 2 m. In the SLR scenarios applied, the tidal current is accelerated as indicated by a reduced M2 phase difference between the seaward and landward ends. Tidal asymmetry in the bay defined by the M2 and M4 phase difference shifts from a mixed flood- and ebb-dominant to ebb-dominant state under SLR below 0.25 m. Using a simplified approach, we showed the impact of tidal asymmetry and current velocity on one component of sediment transport, considering the dominant sediment type, sand. Our results show that the SLR-induced shift to ebb dominance also changes the direction of sand bed-load transport, favoring export under SLR.
Despite the simplifications and assumptions in our study, the findings indicate strong potential SLR-driven effects on the Oosterschelde ecosystem. With negligible freshwater input, the physical transport in the bay is greatly dominated by tides. SLR may increase the tidal amplitude to exceed that in the pre-barrier decades. While the fate of tidal flats needs intensive further studies since fine sediments are not addressed here, our study highlights the spatially variable features of tidal changes under SLR. Comparative studies among basins and sites are desired, and a one-way or two-way model coupling approach seems appropriate in such applications.
The source code for the MARS and GETM model used in this study is available at: https://wwz.ifremer.fr/mars3d/ (last access: 2 March 2020) and https://getm.eu/ (last access: 2 March 2020). Research data are archived at 4TU.Research Data (https://data.4tu.nl/, last access: 2 March 2020) with the following DOI: https://doi.org/10.4121/uuid:c6753aa0-d501-4cbe-9476-a2833d47bfc6 (Jiang et al., 2019b).
LJ ran the GETM simulations, analyzed the results, and initiated the writing of the paper. TG and KS provided guidance and important insights into data interpretation. DI ran the MARS simulation. ABAS conducted the regional SLR projection. All authors participated in the writing and editing of the paper.
The authors declare that they have no conflict of interest.
This work was supported by the collaborative framework of Utrecht University and the Royal Netherlands Institute for Sea Research. Long Jiang was also supported by the Fundamental Research Funds for the Central Universities at Hohai University. The authors acknowledge John M. Huthnance, Stefan Talke, Frank Koesters, and Mick van der Wegen for their thorough review that substantially improved our paper.
This research has been supported by Utrecht University, the Royal Netherlands Institute for Sea Research, and the Fundamental Research Funds for the Central Universities at Hohai University.
This paper was edited by John M. Huthnance and reviewed by Stefan Talke, Frank Koesters, and Mick van der Wegen.
4TU.Research Data: https://data.4tu.nl/, last access: 2 March 2020.
Arbic, B. K. and Garrett, C.: A coupled oscillator model of shelf and ocean tides, Cont. Shelf Res., 30, 564–574, https://doi.org/10.1016/j.csr.2009.07.008, 2010.
Arns, A., Wahl, T., Dangendorf, S., and Jensen, J.: The impact of sea level rise on storm surge water levels in the northern part of the German Bight, Coast. Eng., 96, 118–131, https://doi.org/10.1016/j.coastaleng.2014.12.002, 2015.
Bhuiyan, M. J. A. N. and Dutta, D.: Assessing impacts of sea level rise on river salinity in the Gorai river network, Bangladesh, Estuar. Coast. Shelf S., 96, 219–227, https://doi.org/10.1016/j.ecss.2011.11.005, 2012.
Brown, J. M. and Davies, A. G.: Flood/ebb tidal asymmetry in a shallow sandy estuary and the impact on net sand transport, Geomorphology, 114, 431–439, https://doi.org/10.1016/j.geomorph.2009.08.006, 2010.
Burchard, H., Schuttelaars, H. M., and Geyer, W. R.: Residual sediment fluxes in weakly-to-periodically stratified estuaries and tidal inlets, J. Phys. Oceanogr., 43, 1841–1861, https://doi.org/10.1175/JPO-D-12-0231.1, 2013.
Burchard, H., Schuttelaars, H. M., and Ralston, D. K.: Sediment trapping in estuaries, Annu. Rev. Mar. Sci., 10, 371–395, https://doi.org/10.1146/annurev-marine-010816-060535, 2018.
Carless, S. J., Green, J. M., Pelling, H. E., and Wilmes, S. B.: Effects of future sea-level rise on tidal processes on the Patagonian Shelf, J. Marine Syst., 163, 113–124, https://doi.org/10.1016/j.jmarsys.2016.07.007, 2016.
Chant, R. J., Sommerfield, C. K., and Talke, S. A.: Impact of channel deepening on tidal and gravitational circulation in a highly engineered estuarine basin, Estuaries Coasts, 41, 1587–1600, https://doi.org/10.1007/s12237-018-0379-6, 2018.
Cheng, R. T., Ling, C. H., Gartner, J. W., and Wang, P. F.: Estimates of bottom roughness length and bottom shear stress in South San Francisco Bay, California, J. Geophys. Res., 104, 7715–7728, https://doi.org/10.1029/1998JC900126, 1999.
Chernetsky, A. S., Schuttelaars, H. M., and Talke, S. A.: The effect of tidal asymmetry and temporal settling lag on sediment trapping in tidal estuaries, Ocean Dynam., 60, 1219–1241, https://doi.org/10.1007/s10236-010-0329-8, 2010.
Church, J. A., Clark, P. U., Cazenave, A., Gregory, J. M., Jevrejeva, S., Levermann, A., Merrifield, M. A., Milne, G. A., Nerem, R. S., Nunn, P. D., Payne, A. J. Pfeffer, W. T., Stammer D., and Unnikrishnan, A. S.: Sea Level Change, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013.
Cox, T. J. S., Maris, T., Van Engeland, T., Soetaert, K., and Meire, P.: Critical transitions in suspended sediment dynamics in a temperate meso-tidal estuary, Scientific Reports, 9, 12745 , https://doi.org/10.1038/s41598-019-48978-5, 2019.
de Jonge, V. N., Schuttelaars, H. M., van Beusekom, J. E., Talke, S. A., and de Swart, H. E.: The influence of channel deepening on estuarine turbidity levels and dynamics, as exemplified by the Ems estuary, Estuar. Coast. Shelf S., 139, 46–59, https://doi.org/10.1016/j.ecss.2013.12.030, 2014.
de Pater, P. D.: Effect of removal of the Oosterschelde storm surge barrier, MSc thesis, Delft University of Technology, Delft, the Netherlands, 2012.
Devlin, A. T., Jay, D. A., Talke, S. A., Zaron, E. D., Pan, J., and Lin, H.: Coupling of sea level and tidal range changes, with implications for future water levels, Scientific Reports, 7, 17021, https://doi.org/10.1038/s41598-017-17056-z, 2017.
Dijkstra, Y. M., Schuttelaars, H. M., and Burchard, H.: Generation of exchange flows in estuaries by tidal and gravitational eddy viscosity-shear covariance (ESCO), J. Geophys. Res.-Oceans, 122, 4217–4237, https://doi.org/10.1002/2016JC012379, 2017.
Dijkstra, Y. M., Schuttelaars, H. M., and Schramkowski, G. P.: Can the Scheldt River Estuary become hyperturbid?, Ocean Dynam., 69, 809–827, https://doi.org/10.1007/s10236-019-01277-z, 2019a.
Dijkstra, Y. M., Schuttelaars, H. M., Schramkowski, G. P., and Brouwer, R. L.: Modeling the transition to high sediment concentrations as a response to channel deepening in the Ems River Estuary, J. Geophys. Res.-Oceans, 124, 1578–1594. https://doi.org/10.1029/2018JC014367, 2019b.
Du, J., Shen, J., Zhang, Y. J., Ye, F., Liu, Z., Wang, Z., Wang, Y. P., Yu, X., Sisson, M., and Wang, H. V.: Tidal response to sea-level rise in different types of estuaries: The importance of length, bathymetry, and geometry, Geophys. Res. Lett., 45, 227–235, https://doi.org/10.1002/2017GL075963, 2018.
Duran-Matute, M., Gerkema, T., de Boer, G. J., Nauw, J. J., and Gräwe, U.: Residual circulation and freshwater transport in the Dutch Wadden Sea: a numerical modelling study, Ocean Sci., 10, 611–632, https://doi.org/10.5194/os-10-611-2014, 2014.
Eelkema, M., Wang, Z. B., and Stive, M. J.: Impact of back-barrier dams on the development of the ebb-tidal delta of the Eastern Scheldt, J. Coast. Res., 28, 1591–1605, https://doi.org/10.2112/JCOASTRES-D-11-00003.1, 2012.
Elmilady, H., van der Wegen, M., Roelvink, D., and Jaffe, B. E.: Intertidal area disappears under sea level rise: 250 years of morphodynamic modelling in San Pablo Bay, California, J. Geophys. Res.-Earth, 124, 38–59, https://doi.org/10.1029/2018JF004857, 2019.
Ensing, E., de Swart, H. E., and Schuttelaars, H. M.: Sensitivity of tidal motion in well-mixed estuaries to cross-sectional shape, deepening, and sea level rise, Ocean Dynam., 65, 933–950, https://doi.org/10.1007/s10236-015-0844-8, 2015.
Familkhalili, R. and Talke, S. A.: The effect of channel deepening on tides and storm surge: A case study of Wilmington, NC, Geophys. Res. Lett., 43, 9138–9147, https://doi.org/10.1002/2016GL069494, 2016.
Feng, X., Feng, H., Li, H., Zhang, F., Feng, W., Zhang, W., and Yuan, J.: Tidal responses to future sea level trends on the Yellow Sea shelf, J. Geophys. Res.-Oceans, 124, 7285–7306, https://doi.org/10.1029/2019JC015150, 2019.
FitzGerald, D. M., Fenster, M. S., Argow, B. A., and Buynevich, I. V.: Coastal impacts due to sea-level rise, Annu. Rev. Earth Pl. Sc., 36, 601–647, https://doi.org/10.1146/annurev.earth.35.031306.140139, 2008.
Flather, R. A.: A numerical model investigation of tides and diurnal-period continental shelf waves along Vancouver Island, J. Phys. Oceanogr., 18, 115–139, https://doi.org/10.1175/1520-0485(1988)018<0115:ANMIOT>2.0.CO;2, 1988.
Friedrichs, C. T. and Aubrey, D. G.: Non-linear tidal distortion in shallow well-mixed estuaries: a synthesis, Estuar. Coast. Shelf S., 27, 521–545, https://doi.org/10.1016/0272-7714(88)90082-0, 1988.
Friedrichs, C. T. and Aubrey, D. G.: Tidal propagation in strongly convergent channels, J. Geophys. Res., 99, 3321–3336, https://doi.org/10.1029/93JC03219, 1994.
Friedrichs, C. T., Aubrey, D. G., and Speer, P. E.: Impacts of relative sea-level rise on evolution of shallow estuaries, in: Residual Currents and Long-term Transport, edited by: Cheng, R. T., Springer, New York, 105–122, https://doi.org/10.1007/978-1-4613-9061-9, 1990.
Ganju, N. K. and Schoellhamer, D. H.: Decadal-timescale estuarine geomorphic change under future scenarios of climate and sediment supply, Estuar. Coast., 33, 15–29, https://doi.org/10.1007/s12237-009-9244-y, 2010.
Gerkema, T.: An Introduction to Tides, Cambridge University Press, Cambridge, United Kingdom, 2019.
Gerkema, T. and Duran-Matute, M.: Interannual variability of mean sea level and its sensitivity to wind climate in an inter-tidal basin, Earth Syst. Dynam., 8, 1223–1235, https://doi.org/10.5194/esd-8-1223-2017, 2017.
GETM: A 3D hydrodynamic model for coastal oceans, available at: https://getm.eu/, last access: 2 March 2020.
Geyer, W. R. and MacCready, P.: The estuarine circulation, Annu. Rev. Fluid Mech., 46, 175–197, https://doi.org/10.1146/annurev-fluid-010313-141302, 2014.
Gräwe, U., Burchard, H., Müller, M., and Schuttelaars, H. M.: Seasonal variability in M2 and M4 tidal constituents and its implications for the coastal residual sediment transport, Geophys. Res. Lett., 41, 5563–5570, https://doi.org/10.1002/2014GL060517, 2014.
Haasnoot, M., Kwadijk, J., Van Alphen, J., Le Bars, D., van den Hurk, B., Diermanse, F., van der Spek, A., Oude Essink, G., Delsman, J., and Mens, M.: Adaptation to uncertain sea-level rise; how uncertainty in Antarctic mass-loss impacts the coastal adaptation strategy of the Netherlands, Environ. Res. Lett., 15, 034007, https://doi.org/10.1088/1748-9326/ab666c, 2019.
Haigh I. D., Pickering M. D., Green J. A. M., Arbic B. K., Arns A., Dangendorf, S., Hill, D., Horsburgh, K., Howard, T., Idier, D., Jay, D. A., Jänicke, L., Lee, S. B., Müller, M., Schindelegger, M., Talke, S. A., Wilmes, S.‐B., and Woodworth, P. L.: The tides they are a changin', Rev. Geophys., 57, https://doi.org/10.1029/2018RG000636, 2019.
Haigh, I. D., Wahl, T., Rohling, E. J., Price, R. M., Pattiaratchi, C. B., Calafat, F. M., and Dangendorf, S.: Timescales for detecting a significant acceleration in sea level rise, Nat. Commun., 5, 3635, https://doi.org/10.1038/ncomms4635, 2014.
Hoitink, A. J. F., Hoekstra, P., and Van Maren, D. S.: Flow asymmetry associated with astronomical tides: Implications for the residual transport of sediment, J. Geophys. Res., 108, 3315, https://doi.org/10.1029/2002JC001539, 2003.
Hollebrandse, F. A.: Temporal development of the tidal range in the southern North Sea, MSc thesis, Delft University of Technology, Delft, the Netherlands, available at: https://pdfs.semanticscholar.org/dfb2/742f3009b87125d8e9df7d421a9162e9bcfe.pdf (last access: 2 March 2020), 2005.
Holleman, R. C. and Stacey, M. T.: Coupling of sea level rise, tidal amplification, and inundation, J. Phys. Oceanogr., 44, 1439–1455, https://doi.org/10.1175/JPO-D-13-0214.1, 2014.
Hong, B. and Shen, J.: Responses of estuarine salinity and transport processes to potential future sea-level rise in the Chesapeake Bay, Estuar. Coast. Shelf S., 104, 33–45, https://doi.org/10.1016/j.ecss.2012.03.014, 2012.
Hunt J. N.: Tidal oscillations in estuaries, Geophys. J. Int., 440–455, https://doi.org/10.1111/j.1365-246X.1964.tb03863.x, 1964.
Idier, D., Paris, F., Le Cozannet, G., Boulahya, F., and Dumas, F.: Sea-level rise impacts on the tides of the European Shelf, Cont. Shelf Res., 137, 56–71, https://doi.org/10.1016/j.csr.2017.01.007, 2017.
IFREMER: MARS, available at: https://wwz.ifremer.fr/mars3d/, last access: 2 March 2020.
Jay, D. A.: Green's law revisited: Tidal long-wave propagation in channels with strong topography, J. Geophys. Res., 96, 20585–20598, https://doi.org/10.1029/91JC01633, 1991.
Jay, D. A., Leffler, K., and Degens, S.: Long-term evolution of Columbia River tides, J. Waterway Port Coast., 137, 182–191, https://doi.org/10.1061/(ASCE)WW.1943-5460.0000082, 2010.
Jiang, L., Gerkema, T., Wijsman, J. W., and Soetaert, K.: Comparing physical and biological impacts on seston renewal in a tidal bay with extensive shellfish culture, J. Marine Syst., 194, 102–110, https://doi.org/10.1016/j.jmarsys.2019.03.003, 2019a.
Jiang, L., Gerkema, T., Idier, D., Slangen, A. B. A., and Soetaert, K. E.: Downscaling sea-level rise effects on tides and sediment dynamics in tidal bays, 4TU, Centre for Research Data, Dataset, https://doi.org/10.4121/uuid:c6753aa0-d501-4cbe-9476-a2833d47bfc6, 2019b.
Jiang, L., Soetaert, K., and Gerkema, T.: Decomposing the intra-annual variability of flushing characteristics in a tidal bay along the North Sea, J. Sea Res., 101821, https://doi.org/10.1016/j.seares.2019.101821, 2020.
Katsman, C. A., Sterl, A., Beersma, J. J., van den Brink, H. W., Church, J. A., Hazeleger, W., Kopp, R. E., Kroon, D., Kwadijk, J., Lammersen, R., Lowe J., Oppenheimer, M., Plag, H.-P., Ridley J., von Storch, H., Vaughan, D. G., Vellinga P., Vermeersen, L. L. A., van de Wal, R. S. W., and Weisse, R.: Exploring high-end scenarios for local sea level rise to develop flood protection strategies for a low-lying delta–the Netherlands as an example, Clim. Change, 109, 617–645, https://doi.org/10.1007/s10584-011-0037-5, 2011.
Lanzoni, S. and Seminara, G.: On tide propagation in convergent estuaries. J. Geophys. Res., 103, 30793–30812, https://doi.org/10.1029/1998JC900015, 1998.
Lazure, P. and Dumas, F.: An external–internal mode coupling for a 3D hydrodynamical model for applications at regional scale (MARS), Adv. Water Resour., 31, 233–250, https://doi.org/10.1016/j.advwatres.2007.06.010, 2008.
Lee, S. B., Li, M., and Zhang, F.: Impact of sea level rise on tidal range in Chesapeake and Delaware Bays, J. Geophys. Res.-Oceans, 122, 3917–3938, https://doi.org/10.1002/2016JC012597, 2017.
Lodder, Q. J., Wang, Z. B., Elias, E. P., van der Spek, A. J., de Looff, H., and Townend, I. H.: Future Response of the Wadden Sea Tidal Basins to Relative Sea-Level rise–An Aggregated Modelling Approach, Water, 11, 2198, https://doi.org/10.3390/w11102198, 2019.
Lopes, C. L. and Dias, J. M.: Tidal dynamics in a changing lagoon: Flooding or not flooding the marginal regions, Estuar. Coast. Shelf S., 167, 14–24, https://doi.org/10.1016/j.ecss.2015.05.043, 2015.
Lyard, F., Lefevre, F., Letellier, T., and Francis, O.: Modelling the global ocean tides: modern insights from FES2004, Ocean Dynam., 56, 394–415, https://doi.org/10.1007/s10236-006-0086-x, 2006.
Nnafie, A., De Swart, H. E., Calvete, D., and Garnier, R.: Effects of sea level rise on the formation and drowning of shoreface-connected sand ridges, a model study, Cont. Shelf Res., 80, 32–48, https://doi.org/10.1016/j.csr.2014.02.017, 2014.
Nienhuis, P. H. and Smaal, A. C.: The Oosterschelde estuary, a case-study of a changing ecosystem: an introduction, Hydrobiologia, 282, 1–14, https://doi.org/10.1007/BF00024616, 1994.
Oppenheimer, M., Glavovic, B. C., Hinkel, J., van de Wal, R., Magnan, A. K., Abd-Elgawad, A., Cai, R., Cifuentes-Jara, M., DeConto, R. M., Ghosh, T., Hay, J., Isla, F., Marzeion, B., Meyssignac, B., and Sebesvari, Z.: Sea Level Rise and Implications for Low-Lying Islands, Coasts and Communities, chap. 4, in: IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, edited by: Pörtner, H.-O., Roberts, D. C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., Petzold, J., Rama, B., and Weyer, N. M., in press, available at: https://www.ipcc.ch/srocc/ (last access: 2 March 2020), 2019.
Passeri, D. L.,, Hagen, S. C.Plant, N. G., Bilskie, M. V., Medeiros, S. C., and Alizad, K.: Tidal hydrodynamics under future sea level rise and coastal morphology in the Northern Gulf of Mexico, Earths Future, 4, 159–176, https://doi.org/10.1002/2015EF000332, 2016.
Pawlowicz, R., Beardsley, B., and Lentz, S.: Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE, Comput. Geosci., 28, 929–937, https://doi.org/10.1016/S0098-3004(02)00013-4, 2002.
Pelling, H. E. and Green, J. M.: Impact of flood defences and sea-level rise on the European Shelf tidal regime, Cont. Shelf Res., 85, 96–105, https://doi.org/10.1016/j.csr.2014.04.011, 2014.
Pelling, H. E., Green, J. M., and Ward, S. L.: Modelling tides and sea-level rise: To flood or not to flood, Ocean Model., 63, 21–29, https://doi.org/10.1016/j.ocemod.2012.12.004, 2013a.
Pelling, H. E., Uehara, K., and Green, J. A. M.: The impact of rapid coastline changes and sea level rise on the tides in the Bohai Sea, China, J. Geophys. Res.-Oceans, 118, 3462–3472, https://doi.org/10.1002/jgrc.20258, 2013b.
Pickering, M. D., Wells, N. C., Horsburgh, K. J., and Green, J. A. M.: The impact of future sea-level rise on the European Shelf tides, Cont. Shelf Res., 35, 1–15, https://doi.org/10.1016/j.csr.2011.11.011, 2012.
Pickering, M. D., Horsburgh, K. J., Blundell, J. R., Hirschi, J. M., Nicholls, R. J., Verlaan, M., and Wells, N. C.: The impact of future sea-level rise on the global tides, Cont. Shelf Res., 142, 50–68, https://doi.org/10.1016/j.csr.2017.02.004, 2017.
Prandle, D.: How tides and river flows determine estuarine bathymetries, Prog. Oceanogr., 61, 1–26, https://doi.org/10.1016/j.pocean.2004.03.001, 2004.
Ralston, D. K., Talke, S., Geyer, W. R., Al-Zubaidi, H. A. M., and Sommerfield, C. K.: Bigger tides, less flooding: Effects of dredging on barotropic dynamics in a highly modified estuary, J. Geophys. Res.-Oceans, 124, 196–211, https://doi.org/10.1029/2018JC014313, 2019.
Rasquin, C., Seiffert, R., Wachler, B., and Winkel, N.: The significance of coastal bathymetry representation for modelling the tidal response to mean sea level rise in the German Bight, Ocean Sci., 16, 31–44, https://doi.org/10.5194/os-16-31-2020, 2020.
Ray, R. D.: Secular changes of the M2 tide in the Gulf of Maine, Cont. Shelf Res., 26, 422–427, https://doi.org/10.1016/j.csr.2005.12.005, 2006.
Ross, A. C., Najjar, R. G., Li, M., Lee, S. B., Zhang, F., and Liu, W.: Fingerprints of sea level rise on changing tides in the Chesapeake and Delaware Bays, J. Geophys. Res.-Oceans, 122, 8102–8125, https://doi.org/10.1002/2017JC012887, 2017.
Savenije, H. H. G. and Veling, E. J. M.: Relation between tidal damping and wave celerity in estuaries, J. Geophys. Res., 110, C04007, https://doi.org/10.1029/2004JC002278, 2005.
Schulz, K. and Gerkema, T.: An inversion of the estuarine circulation by sluice water discharge and its impact on suspended sediment transport, Estuar. Coast. Shelf S., 200, 31–40, https://doi.org/10.1016/j.ecss.2017.09.031, 2018.
Slangen, A. B. A., Carson, M., Katsman, C. A., Van de Wal, R. S. W., Köhl, A., Vermeersen, L. L. A., and Stammer, D.: Projecting twenty-first century regional sea-level changes, Clim. Change, 124, 317–332, https://doi.org/10.1007/s10584-014-1080-9, 2014.
Speer, P. E. and Aubrey, D. G.: A study of non-linear tidal propagation in shallow inlet/estuarine systems Part II: Theory, Estuar. Coast. Shelf S., 21, 207–224, https://doi.org/10.1016/0272-7714(85)90097-6, 1985.
Sutherland, G., Garrett, C., and Foreman, M.: Tidal resonance in Juan de Fuca Strait and the Strait of Georgia, J. Phys. Oceanogr., 35, 1279–1286, https://doi.org/10.1175/JPO2738.1, 2005.
Talke, S. A. and Jay, D. A.: Changing Tides: The Role of Natural and Anthropogenic Factors, Annu. Rev. Mar. Sci., 12, 14.1–14.31, https://doi.org/10.1146/annurev-marine-010419-010727, 2020.
Talke, S. A., de Swart, H. E., and De Jonge, V. N.: An idealized model and systematic process study of oxygen depletion in highly turbid estuaries, Estuar. Coast., 32, 602–620, https://doi.org/10.1007/s12237-009-9171-y, 2009.
Taylor, K. E.: Summarizing multiple aspects of model performance in a single diagram, J. Geophys. Res., 106, 7183–7192, https://doi.org/10.1029/2000JD900719, 2001.
ten Brinke, W. B. M., Dronkers, J., and Mulder, J. P. M.: Fine sediments in the Oosterschelde tidal basin before and after partial closure, Hydrobiologia, 282, 41–56, https://doi.org/10.1007/BF00024620, 1994.
van der Wegen, M.: Numerical modeling of the impact of sea level rise on tidal basin morphodynamics, J. Geophys. Res.-Earth, 118, 447–460, https://doi.org/10.1002/jgrf.20034, 2013.
van der Wegen, M., Dastgheib, A., Jaffe, B. E., and Roelvink, D.: Bed composition generation for morphodynamic modeling: case study of San Pablo Bay in California, USA, Ocean Dynam., 61, 173–186, https://doi.org/10.1007/s10236-010-0314-2, 2011.
van der Wegen, M., Jaffe, B., Foxgrover, A., and Roelvink, D.: Mudflat morphodynamics and the impact of sea level rise in South San Francisco Bay, Estuar. Coast., 40, 37–49, https://doi.org/10.1007/s12237-016-0129-6, 2017.
van Goor, M. A., Zitman, T. J., Wang, Z. B., and Stive, M. J. F.: Impact of sea-level rise on the morphological equilibrium state of tidal inlets, Mar. Geol., 202, 211–227, https://doi.org/10.1016/S0025-3227(03)00262-7, 2003.
van Maren, D. S., Hoekstra, P., and Hoitink, A. J. F.: Tidal flow asymmetry in the diurnal regime: bed-load transport and morphologic changes around the Red River Delta, Ocean Dynam., 54, 424–434, https://doi.org/10.1007/s10236-003-0085-0, 2004.
van Rijn, L. C.: Analytical and numerical analysis of tides and salinities in estuaries; part I: tidal wave propagation in convergent estuaries, Ocean Dynam., 61, 1719–1741, https://doi.org/10.1007/s10236-011-0453-0, 2011.
van Rijn, L., Grasmeijer, B., and Perk, L.: Effect of channel deepening on tidal flow and sediment transport: part I—sandy channels, Ocean Dynam., 68, 1457–1479, https://doi.org/10.1007/s10236-018-1204-2, 2018.
Vermeersen, B. L. A., Slangen, A. B. A., Gerkema, T., Baart, F., Cohen, K. M., Dangendorf, S., Duran-Matute, M., Frederikse, T., Grinsted, A., Hijma, M. P., Jevrejeva, S., Kiden, P., Kleinherenbrink, M., Meijles, E. W., Palmer, M. D., Rietbroek, R., Riva, R. E. M., Schulz, E., Slobbe, D. C., Simpson, M. J. R., Sterlini, P., Stocchi, P., van de Wal R. S. W., and van der Wegen, M.: Sea-level change in the Dutch Wadden Sea, Neth. J. Geosci., 97, 79–127, https://doi.org/10.1017/njg.2018.7, 2018.
Vroon, J.: Hydrodynamic characteristics of the Oosterschelde in recent decades, Hydrobiologia, 282, 17–27, https://doi.org/10.1007/BF00024618, 1994.
Winterwerp, J. C. and Wang, Z. B.: Man-induced regime shifts in small estuaries–I: theory. Ocean Dynam., 63, 1279–1292, https://doi.org/10.1007/s10236-013-0662-9, 2013.
Winterwerp, J. C., Wang, Z. B., van Braeckel, A., van Holland, G., and Kösters, F.: Man-induced regime shifts in small estuaries–II: a comparison of rivers, Ocean Dynam., 63, 1293–1306, https://doi.org/10.1007/s10236-013-0663-8, 2013.
Zhang, W., Ruan, X., Zheng, J., Zhu, Y., and Wu, H.: Long-term change in tidal dynamics and its cause in the Pearl River Delta, China, Geomorphology, 120, 209–223, https://doi.org/10.1016/j.geomorph.2010.03.031, 2010.
Zhao, C., Ge, J., and Ding, P.: Impact of sea level rise on storm surges around the Changjiang Estuary, J. Coastal Res., 68, 27–34, https://doi.org/10.2112/SI68-004.1, 2014.
Zhou, X., Zheng, J., Doong, D.-J., and Demirbilek, Z.: Sea level rise along the East Asia and Chinese coasts and its role on the morphodynamic response of the Yangtze River estuary, Ocean Eng., 71, 40–50, https://doi.org/10.1016/j.oceaneng.2013.03.014, 2013.